20172328 2018-2019《Java软件结构与数据结构》第一周学习总结

20172328 2018-2019《Java软件结构与数据结构》第一周学习总结

概述 Generalization

本周学习了软件质量、数据结构以及算法分析的具体内容，主要依托于所用教材的第一章和第二章。

教材学习内容总结 A summary of textbook

  • 第一章：概述

  • 1.1软件质量

  • 软件工程：是一门关于高质量软件开发的技术和理论的学科。

  • 软件工程的目标：解决正确性问题、按时且在预算之内给出解决方案、给出高质量的解决方案、以合情合理的方式完成上面事情。

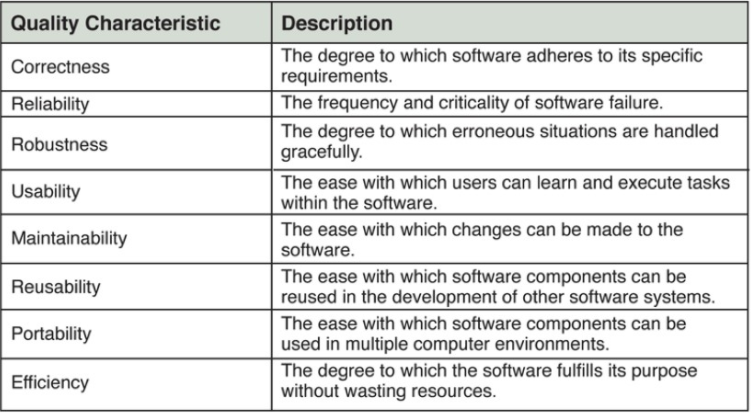
  • 高质量软件的特征

  • 重要解读：

  • 有关可靠性：可靠的软件很少发生故障，即使发生了故障，也可以将该故障的影响降到最低。

  • 有关可维护性：软件系统必须经过细心设计、编码和文档说明，以便为开发人员、维护人员和用户的工作提供支持。

  • 有关可移植性：Java的源代码被编译成了字节码，这是一种低级语言，他不是任何特定CPU的机器语言。字节码运行在Java虚拟上（JVM）。JVM是一种解释并执行字节码的软件。

  • 有关运行效率：软件必须高效地使用诸如CPU时间和存储器之类的资源。

  • 1.2数据结构

  • 数据结构：计算机存储、组织数据的形式。

  • 程序 = 数据结构 + 算法

  • 软件 = 程序 + 软件工程

  • Java工具包提供了强大的数据结构。常见的数据结构有数组（Array）、栈（Stack）、队列（Queue）、链表（Linked list）、树（Tree）、哈希表（Hash）、散列表（Hash Table）等。

  • 栈会颠倒数据集的结构，而队列可以保持数据集的结构。

  • 可用于给数列集排队的常用数据结构有有序列表、堆和散列表。

  • 第二章：算法分析

  • 2.1算法效率分析

  • 算法分析：计算机科学中主要关注软件算法效率的主题。算法分析是计算机科学的基础。

  • 2.2增长函数与大O记法

  • 增长函数：表示与该问题大小相对应的时间或者空间的使用，表示问题（n）大小与我们希望最优化的值之间的关系。该函数表示了该算法的事件复杂度或空间复杂度。

  • 渐进复杂度：称为算法的阶次。如书中示例，第二个洗盘子的算法具有阶次为n2的时间复杂度，记为O（n2），这种记法称为O()或者大O记法。算法的阶次是忽略该算法的的增长函数中的常量和其他次要项，只保留主项而得出的。

  • 一些增长函数及其渐进复杂度[图片展示]

  • 从而算法的阶次为增长函数提供了一个上界。

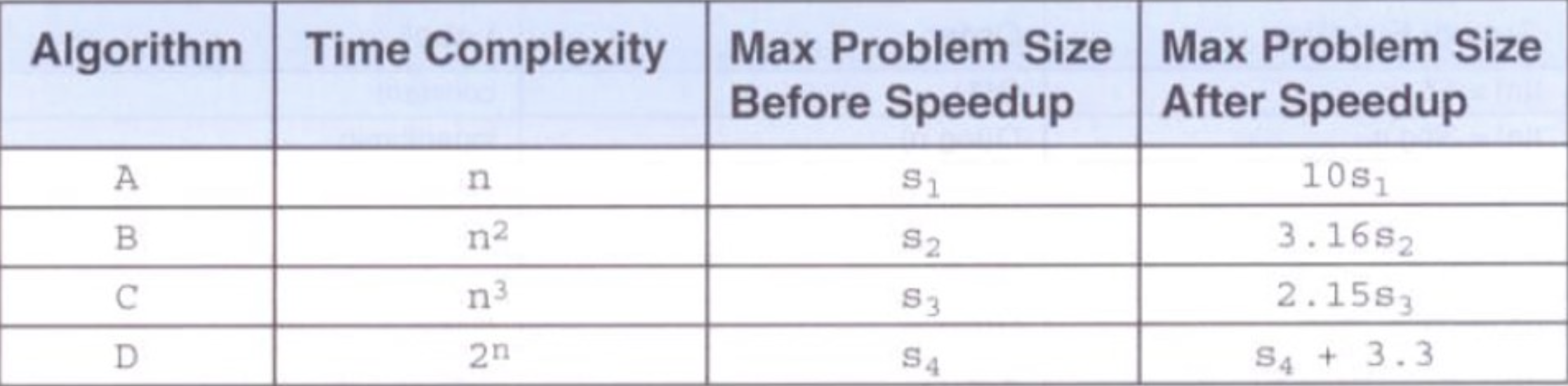
  • 2.3增长函数的比较

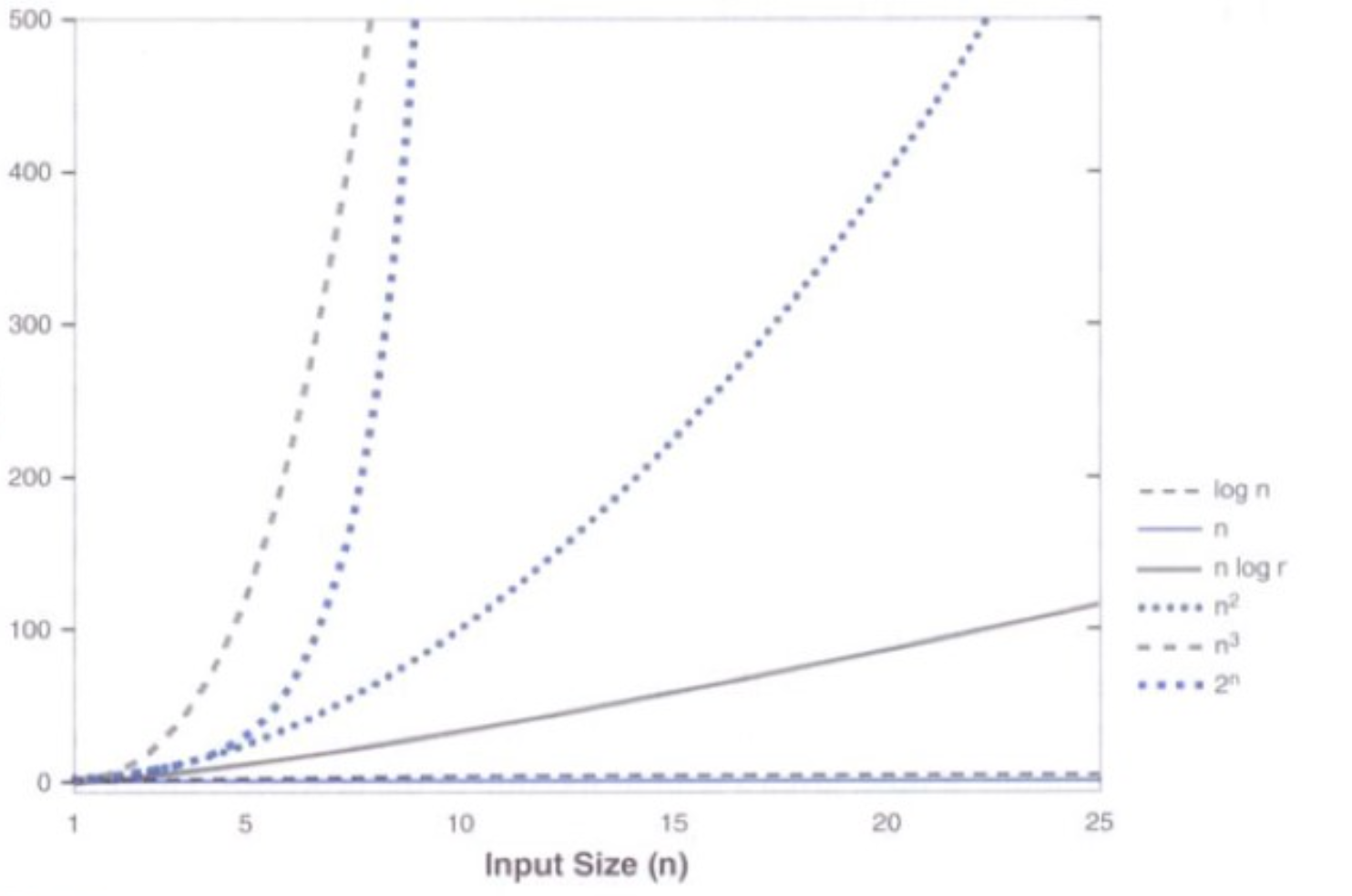
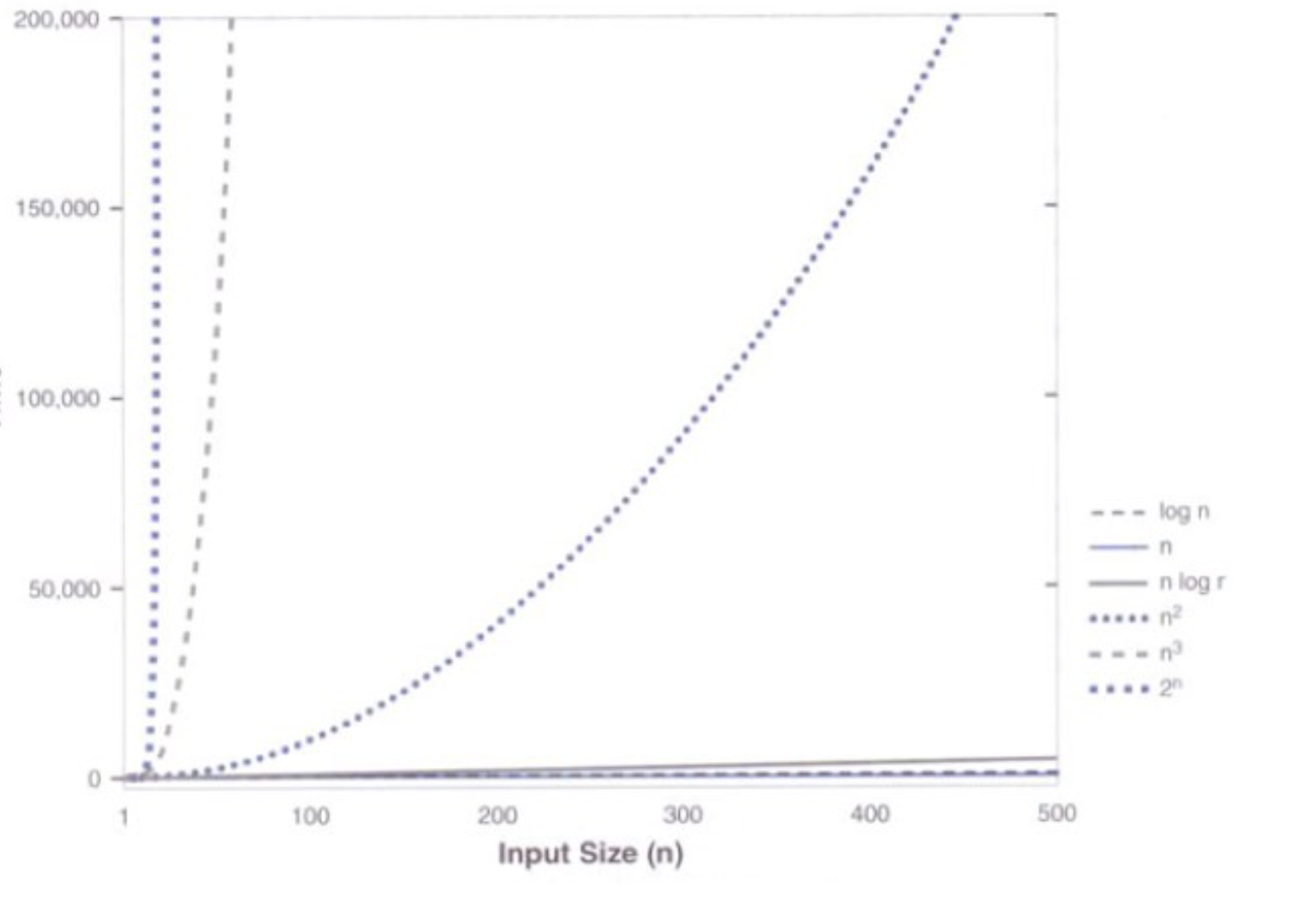
  • 标注：√10≈3.162277660168379、³√10≈2.1544、log₂(10)=lg(10)/lg(2)=1/lg(2)=3.321928，从最后一组数据来看，其实问题的关键不是提速CPU（因为提速处理器后帮助却小的可怜），而是要在算法上简化问题，大大提高程序运行的速度。

  • 增长函数的比较图

  • 2.4时间复杂度分析

  • 2.4.1循环运行的复杂度分析

  • 要分析某个算法的阶次，常常需要去确定某个特定语句和某个语句集运行的次数。要分析循环运行，首先要确定该循环体的阶次n，然后用该循环运行的次数乘以它。记请住，n是表示问题的大小。

  • 就算循环有时会跳过几个数，增长函数变了，但常数不影响渐进复杂度，因此阶次不变。

  • 2.4.2嵌套循环的复杂度分析

  • 分析嵌套循环时，将内存循环和外层循环都要兼顾到，并且用乘法来计算复杂度。

  • 方法调用的复杂度分析：与循环体的复杂度有关。

教材学习中的问题和解决过程 Problem and countermeasure

  • 问题：在做老师课上的考试题时，一直觉得有道题运行次数是n（n-1），故复杂度应该表示为O（n（n-1）），但当时在书本实例中都没有看到有这种表示，先做了题，但没有深入了解。
  • 解决：其实这个问题是自己没有认真看书的后果。书本15页下有这样一段话：

在这种情况下，内层循环索引被初始化为外层循环索引的当前值。外层循环运行了n次，内层循环第一次被执行n次，第二次执行n-1次，等等……但是，记住，我们只对主项感兴趣，而忽视其他常数项或其他任何次要项。如果复杂度是线性的，则不管经过多少个元素，其阶次依旧是O(n)，因此，上面的代码的复杂度为O（n^2）。

课后习题作答 Exercise

  • EX 2.1：下列增长函数的阶次是多少？
    • a.10n^2+100n+1000
    • 解答：阶次为：n^2。
    • b.10n^3-7
    • 解答：阶次为：n^3
    • c.2n+100n3
    • 解答：阶次为：n^3
    • d.n^2 ·log(n)
    • 解答：阶次：n^2 ·log(n)
  • EX 2.4：请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
        {
            System.out.println(count,count2);
        }
}
  • 解答：由内循环需要进行的次数是n/2，外循环需要进行的次数是n，故增长函数为F(n)=(n2)/2，阶次为n2
  • EX 2.5：请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
    for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
        {
            System.out.println(count,count2);
        }
}
  • 解答：由内循环进行的次数是log₂（n-1），外循环需要进行的次数是n，故增长函数为F(n)=n·log₂(n-1)，又因阶数与增长函数的最高阶项有关，要忽略次项与常数项，所以阶次为n·log2(n)。

结对及互评 Group Estimate

-20172301
-20172304

点评模板：

  • 博客中值得学习的或问题：
    • 20172301：博客果然又很精彩，在教材学习中的问题和解决过程中花费了很多精力学习了一些本章中浅尝辄止的内容。优秀👏！
    • 20172304：这次段志轩同学交的最早，而且博客风格较上学期有了很大改变。内容也非常详实，非常好的新学期态势，加油💪！
    • 对我们小组新学期的想法：三人行，必有我师焉。这学期课程量少，那就没有理由再不好好学习专业课。嘿！让我们一起携手努力吧😁

其他（感悟、思考等，可选）Else

莫听穿林打叶声，何妨吟啸且徐行。

学习进度条 Learning List

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积）
目标 5000行 30篇 400小时
第一周 0/0 1/1 8/8

参考资料 Reference

posted @ 2018-09-09 10:12  虹澄清晓  阅读(420)  评论(2)  编辑  收藏  举报
页尾