卷积神经网络(CNN)详解

　　神经网络不是具体的算法，而是一种模型构造的思路或者方式，全连接神经网络每一个神经元节点的输入都来自于上一层的每个神经元的输出，好处在于每个输入维度的信息都会传播到其后的任意一个结点中去，会最大程度地让整个网络中的节点都不会“漏掉”这个维度所贡献的因素。不过他的缺点更加明显，那就是整个网络由于都是“全连接”方式，所以$w$和$b$参数格外的多，这就使得训练过程中说要更新的参数权重非常多，整个网络训练的收敛会非常慢。于是发明了卷积神经网络（Convolutional Neural Network, CNN）。

　　卷积神经网络同样是一种前馈神经网络，他的神经元可以响应一部分覆盖范围内的周围单元，在大规模的模式识别有很好的性能表现，该网络可以避免对图片的复杂前期预处理，直接输入原始图像。

全连接网络的局限性

参数数量太多
没有利用像素之间的位置信息
网络层数限制

卷积网络的优点

局部连接：这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。
权值共享：一组连接可以共享同一个卷积核权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。
下采样：可以使用stride来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

卷积的数学定义

　　函数$f$和$g$的卷积表示经过翻转和平移的重叠部分的面积。

$$h(x)=f(x)*g(x)=\int_{-\infty }^{+\infty }f(t)g(x-t)dt$$

$f(t)$先不动，$g(-t)$相当于$g(t)$函数的图像沿着$y$轴$(t=0)$做一次翻转。$g(x-t)$相当于$g(-t)$的整个图像沿着$t$轴向右平移$x$个单位。卷积的值等于$f(t)$和$g(x-t)$相乘后与$y=0$轴围的面积。

标准卷积

Pytorch文档中Conv2d模块
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
in_channels ( int ) — 输入图像中的通道数

out_channels ( int ) — 卷积产生的通道数

kernel_size ( int or tuple ) — 卷积核的大小

stride ( int or tuple , optional ) — 卷积的步幅。默认值：1

padding ( int or tuple , optional ) — 添加到输入两侧的零填充。默认值：0

dilation ( int or tuple , optional ) — 内核元素之间的间距。默认值：1

groups ( int , optional ) — 从输入通道到输出通道的阻塞连接数。默认值：1

bias ( bool , optional ) — 如果True，则向输出添加可学习的偏差。默认：True

输入：$(N, C_{in}, H_{in}, W_{in})$

输出：$(N,C_{out},H_{out},W_{out})$

$$H_{out}=\frac{H_{in}+2*padding[0]-dilation[0]*(K[0]-1)-1}{stride[0]}+1$$

$$W_{out}=\frac{W_{in}+2*padding[1]-dilation[1]*(K[1]-1)-1}{stride[1]}+1$$

conv2d.weight：$(C_{out},\frac{C_{in}}{groups},K[0],K[1])$

conv2d.bias：$(C_{out},)$

卷积神经网络中的卷积过程是：卷积核(kernel)对输入矩阵进行从左到右，从上到下卷积乘积，得到feature map的过程。卷积神经网络的权重参数在卷积核上，卷积核的计算公式为：$f(x)=\sum _i^{keral\_size}w_ix_i+b$。

　　卷积过程如下所示：我们先假设有这样一幅图像 (通道数, 高度，宽度)，大小为：(1, 5, 5)。卷积核大小为(3, 3)，偏置项为0，卷积后，得到一个(1, 3, 3)的卷积输出(feature map)。

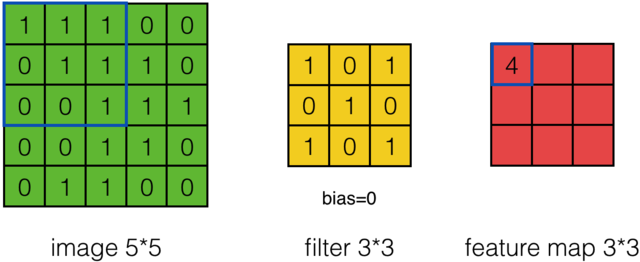
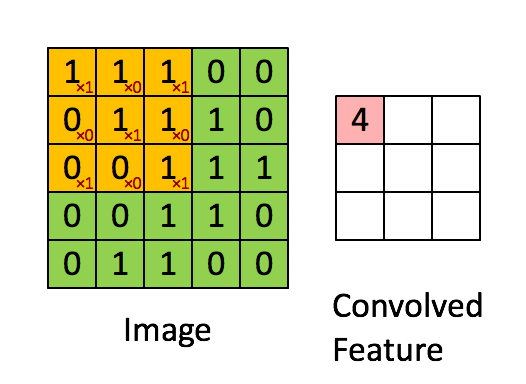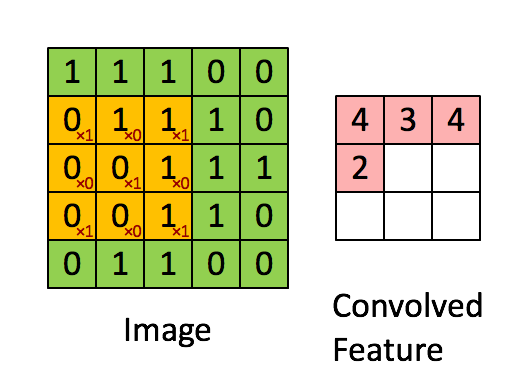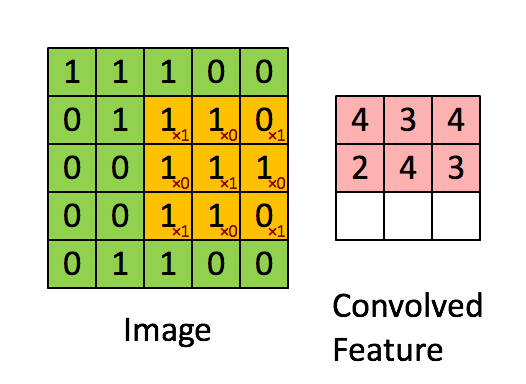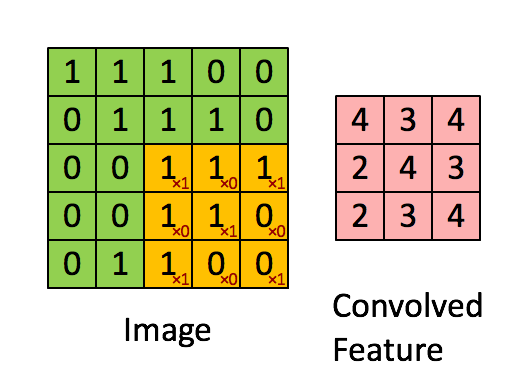
feature map的第一个值的计算过程为：

$$feature\ map(1)=(1*1)+(0*1)+(1*1)+(0*0)+(1*1)+(1*0)+(0*1)+(0*0)+(1*1)+0=4$$

由上图可知：

输入图像的边缘像素因其处于边缘位置，因此无法参与卷积计算；
卷积计算实质上是对图像进行了下采样 (down sampling)操作，这个过程就叫做特征提取，同时也是一种信息压缩。
卷积核中的权重系数$w_i$是通过数据驱动机制学习得到，卷积核的shape可以是3*3，也可以是1*1，不要求一定是方形的，但是一般要求卷积核大小是奇数，选择奇数大小的内核是因为中心像素周围存在对称性。

多输入、多输出

　　对于彩色图片有RGB三个通道，需要处理多输入通道的场景，相应的输出特征图往往也会具有多个通道。而且在神经网络的计算中常常是把一个batch的样本放在一起计算

多输入

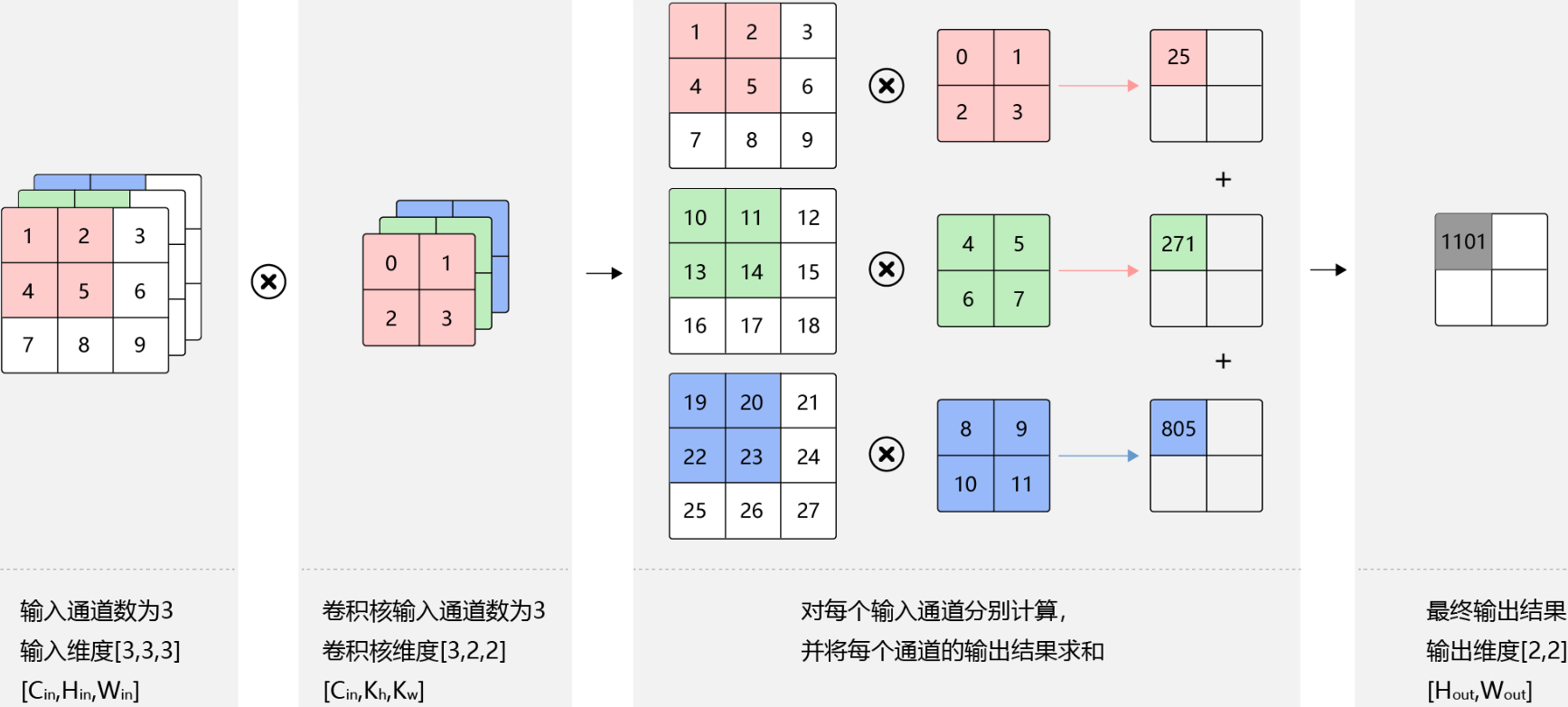
　　假设输入图片的通道数为$C_{in}$，输入数据的形状是$C_{in}×H_{in}×W_{in}$。卷积核的数量等于输入通道数，形状是$C_{in}×K_h×H_w$。对任一通道$C_{in}∈[0,C_{in})$，分别用大小为$K_h×K_w$的卷积核在大小为$H_{in}×W_{in}$的二维数组上做卷积。将这$C_{in}$个通道的计算结果相加，得到的是一个形状为$H_{out}×W_{out}$的二维数组。

多输出

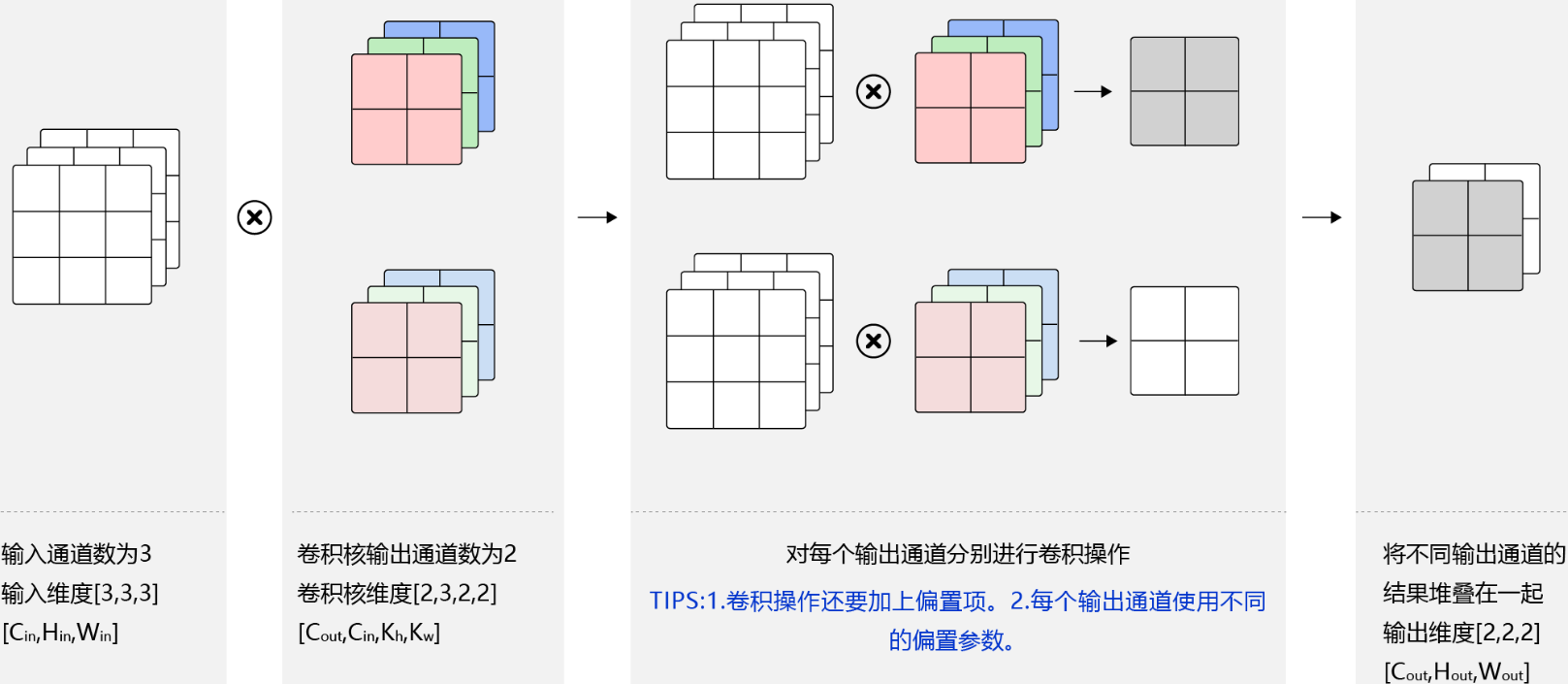
　　卷积操作的输出特征图也会具有多个通道$C_{out}$，这时我们需要设计$C_{out}$个维度为$C_{in}×K_h×K_w$的卷积核，卷积核数组的维度是$C_{out}×C_{in}×K_h×K_w$。对任一输出通道，分别使用上面描述的形状为$C_{in}×K_h×K_w$的卷积核对输入图片做卷积。将这$C_{out}$个形状为$H_{out}×W_{out}$的二维数组拼接在一起，形成维度为$C_{out}×H_{out}×W_{out}$的三维数组。

输出通道的数目通常也被称作卷积核的个数，这里有两个卷积核。
红绿蓝代表第一个卷积核的三个输入通道；浅红浅绿浅蓝代表第二个卷积核的三个输入通道。

步长(Stride)

　　Stride定义为卷积核每次滑动的长度。默认情况下，内核从左到右移动，从上到下逐像素移动。但这种步长也可以改变。通常用于对输出通道进行下采样。例如，stride=(2,2)，卷积核水平方向每次移动2步，垂直方向每次移动2步，这导致输入被下采样2倍。

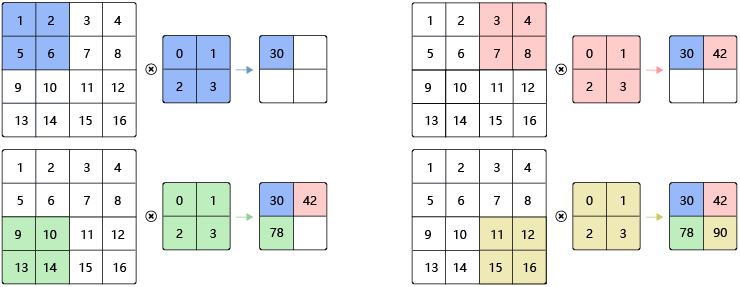
步幅为2的卷积过程

当高和宽方向的步幅分别为$S_h$和$S_w$时，输出特征图尺寸的计算公式是：

$$H_{out} =\frac{H+2 P_h-K_h}{S_h}+1$$

$$W_{out} =\frac{W+2 P_w-K_w}{S_w}+1$$

填充(Padding)

Padding是指在边缘像素点周围填充 “0”，Padding大概有两种目的

保持边界信息。如果不加Padding的话，最边缘的信息其实仅仅被卷积核扫描了一遍，而图片中间的像素点信息被扫描了多遍，在一定程度上就增加了边界上信息的参考程度。
保持输出和输入shape一致：如果输入的图片尺寸有差异，可以通过Padding来进行补齐，使得输出和输入的shape一致

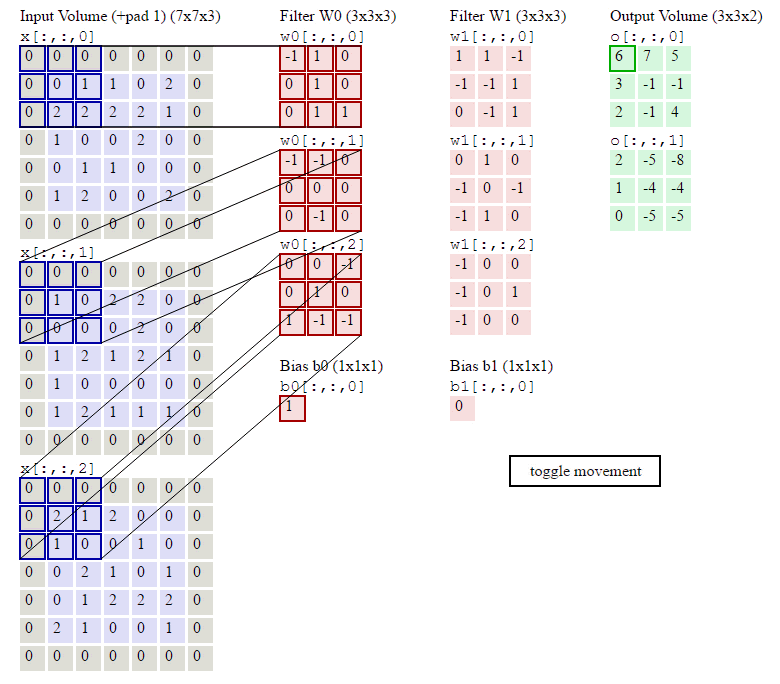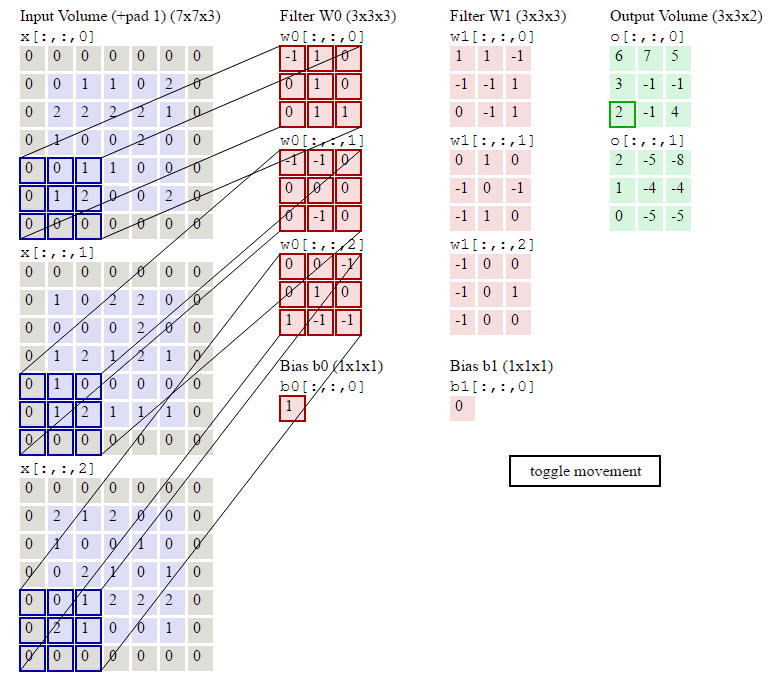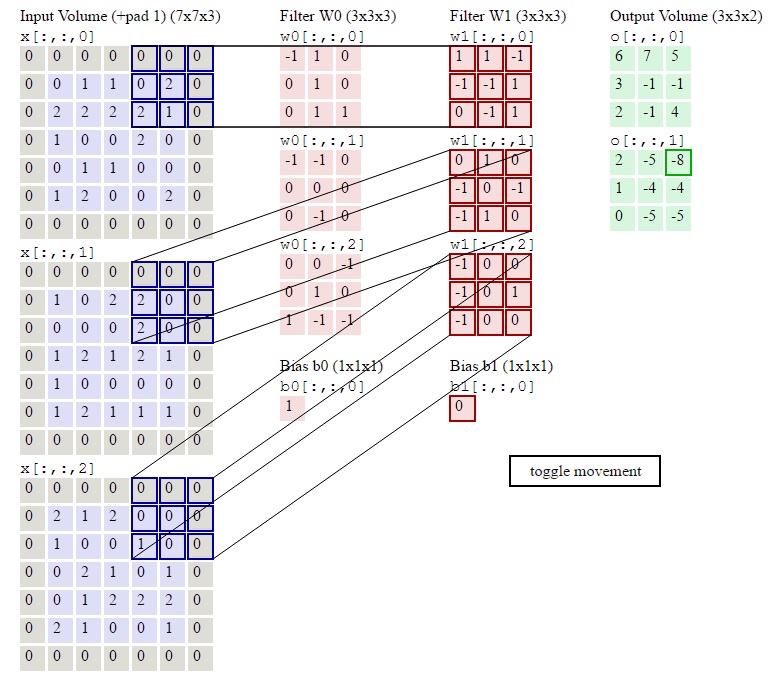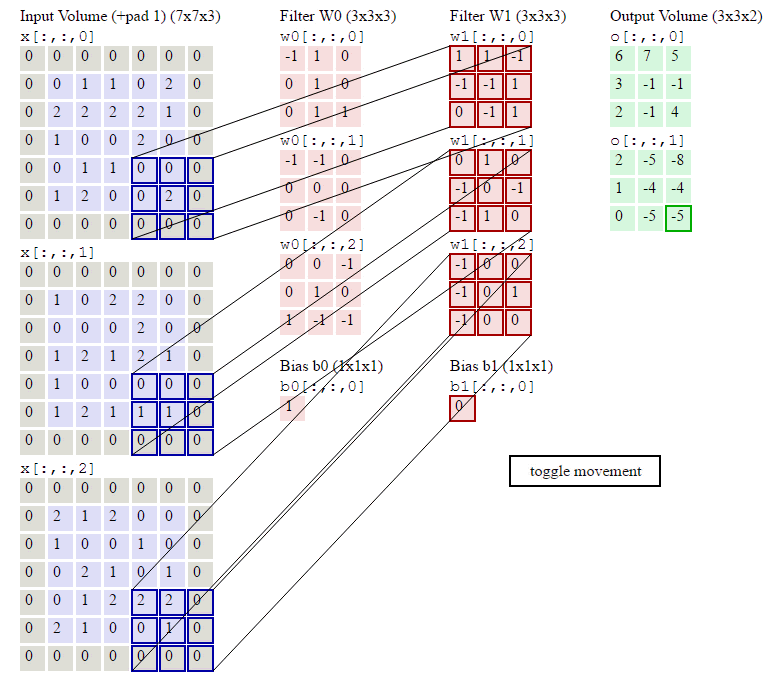
在卷积计算过程中，通常会在高度或者宽度的两侧采取等量填充，即

$$H_{out}=H_{in}+2P_h-K_h+1$$

$$W_{out}=W_{in}+2P_w-K_w+1$$

为了便于padding以及中心像素存在对称性，卷积核大小通常使用1，3，5，7这样的奇数，这样如果使用的填充大小为$P=(K−1)/2$，则可以使得卷积之后图像尺寸不变。例如当卷积核大小为3时，padding大小为1，卷积之后图像尺寸不变；同理，如果卷积核大小为5，padding大小为2，也能保持图像尺寸不变。

1*1卷积

1×1卷积，与标准卷积完全一样，唯一的特殊点在于卷积核的尺寸是1×1，也就是不去考虑输入数据局部信息之间的关系，而把关注点放在不同通道间。当输入矩阵的尺寸为3×3，通道数也为3时，使用4个1×1卷积核进行卷积计算，最终就会得到与输入矩阵尺寸相同，通道数为4的输出矩阵，如图所示。

1×1卷积的作用

实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度（宽、高、多通道），所以1×1卷积实际上就是对每个像素点，在不同的通道上进行线性组合，从而整合不同通道的信息。
对卷积核通道数进行降维和升维，减少参数量。经过1×1卷积后的输出保留了输入数据的原有平面结构，通过调控通道数，从而完成升维或降维的作用。
利用1×1卷积后的非线性激活函数，在保持特征图尺寸不变的前提下，大幅增加非线性

扩张(dilation)卷积

　　扩张卷积(dilation Convolution)也被称为扩张卷积，在某种程度上是膨胀卷积核的宽度，默认情况下是1，它对应于卷积核内每个像素之间的偏移量。dilation一定程度上扩大了特征选取的范围，也就是通常人们所说的感受野。

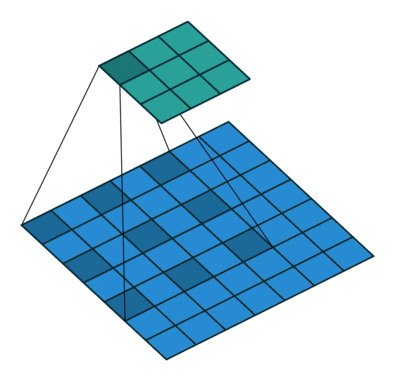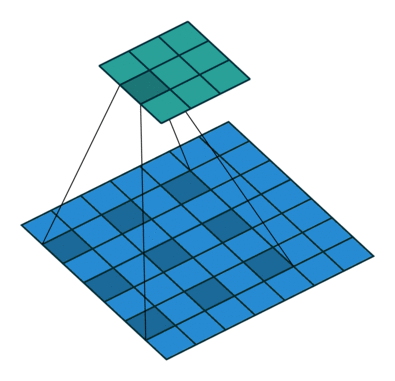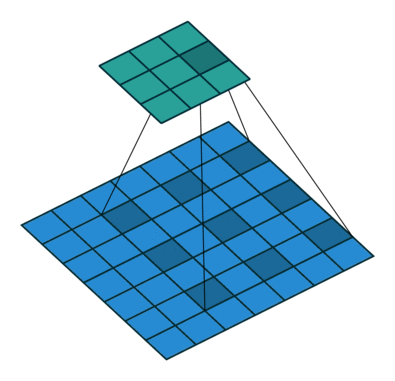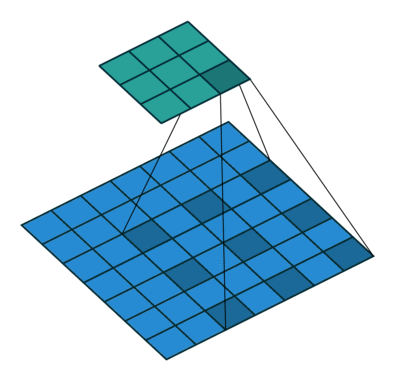
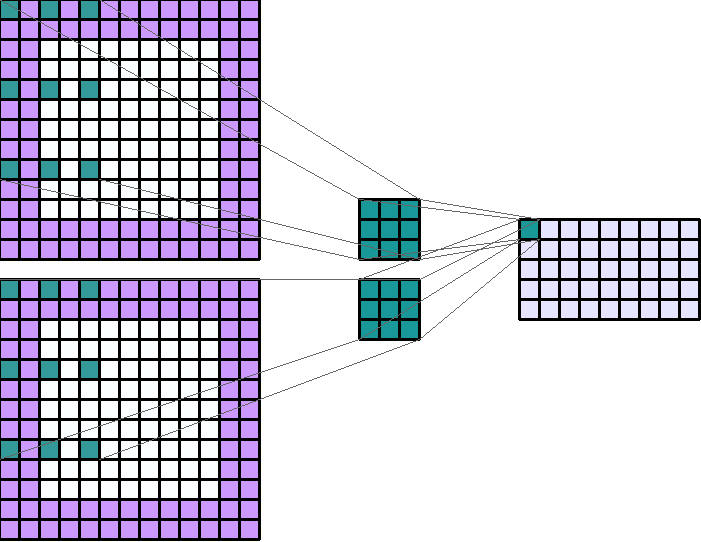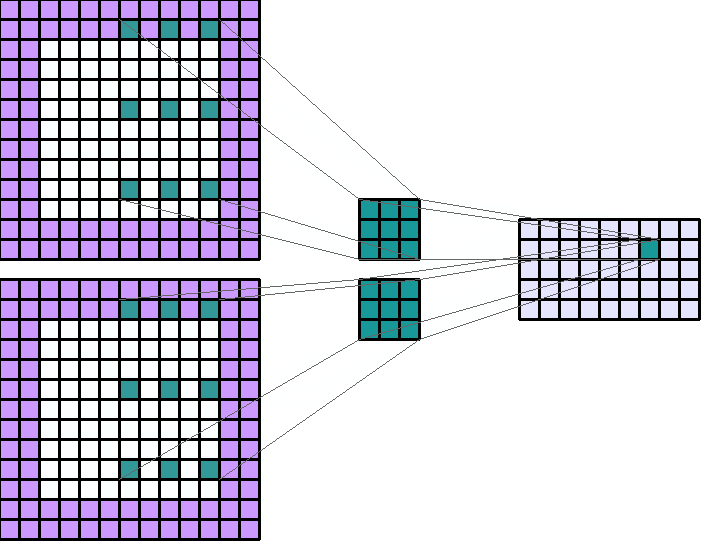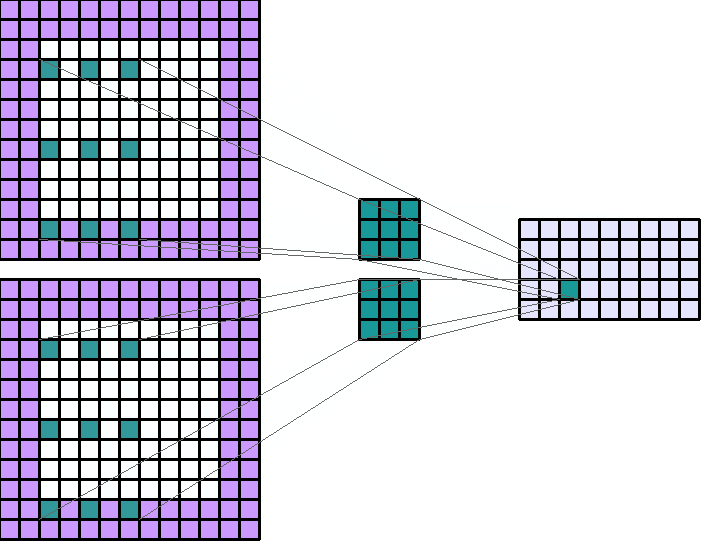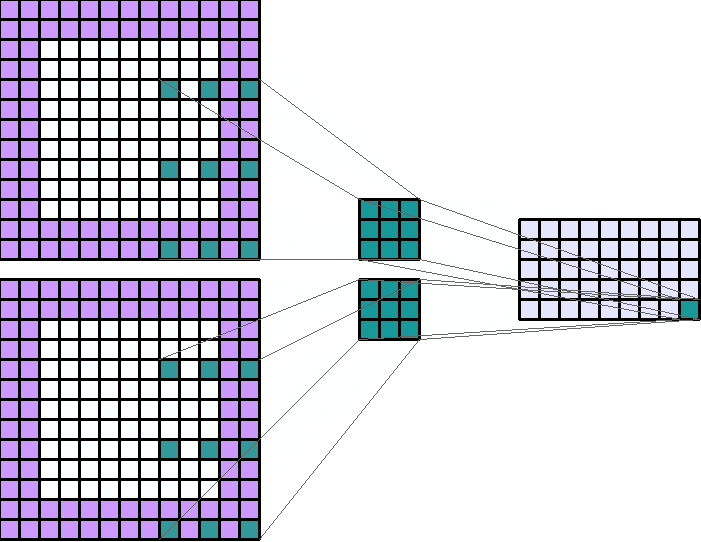
左图：dilation=2的卷积核

右图：输入形状：(2, 7, 7) — 输出形状：(1, 1, 5) — K : (3, 3) — P : (1, 1) — S : (1, 1) — D : (4 , 2) — G : 1

上图原本卷积核shape为(3, 3)，dilation为(4,2)，那么输入通道上内核的感受野会扩大为 H：(3-1)*4+1=9，W：(3-1)*2+1=5。卷积核的作用范围扩大，参数数量不变，有些被包括的点实际上并未参与运算，因此dilation对参数数量没有影响，对计算时间的影响非常有限。

对于卷积核大小为$k$，扩张率为$r$的空洞卷积，感受野$F$的计算公式为：

$$F=k+(k-1)(r-1)$$

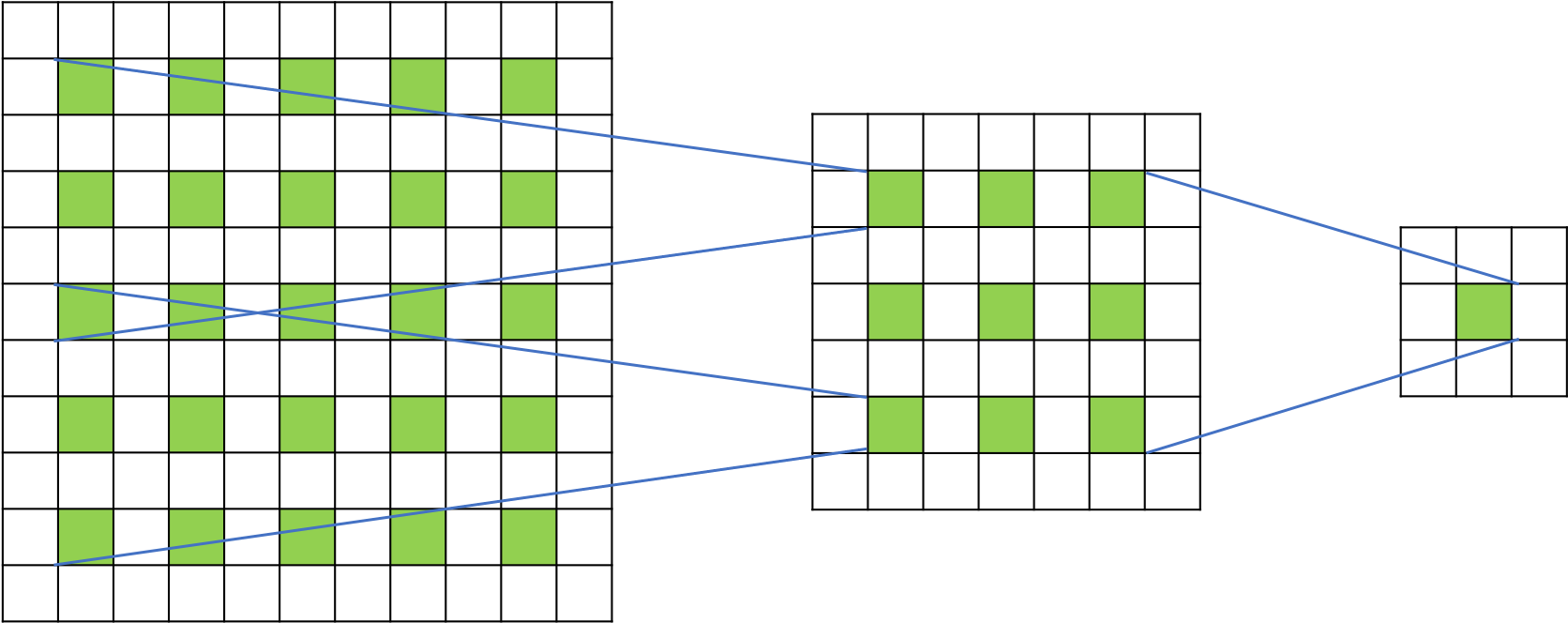
其中，通过一层空洞卷积后，感受野大小为5×5，而通过两层空洞卷积后，感受野的大小将会增加到9×9。

分组(Groups)卷积

　　对于标准卷积：输入矩阵尺寸为$H_1×W_1×C_1$，当标准卷积核的尺寸为$h_1×w_1×C_1$，共有$C_2$个标准卷积核时，标准卷积会对完整的输入数据进行运算，最终得到的输出矩阵尺寸为$H_2×W_2×C_2$。这里我们假设卷积运算前后的特征图尺寸保持不变。

　　对于分组卷积：将输入数据的输入通道分成$g$组，宽和高保持不变，即将每$\frac{C_1}{g}$个通道的数据分为一组。因为输入数据发生了改变，相应的卷积核也需要进行对应的变化，即每个卷积核的输入通道数也就变为了$\frac{C_1}{g}$，同样卷积核的大小是不需要改变的。每组的卷积核个数也由原来的$C_2$变为$\frac{C_2}{g}$。对于每个组内的卷积运算，同样采用标准卷积运算的计算方式，这样就可以得到 g组尺寸为$H_2×W_2×\frac{C_2}{g}$的输出矩阵，最终将这$g$组输出矩阵进行拼接就可以得到最终的结果。这样拼接完成后，最终的输出尺寸就可以保持不变，仍然是$H_2×W_2×C_2$。

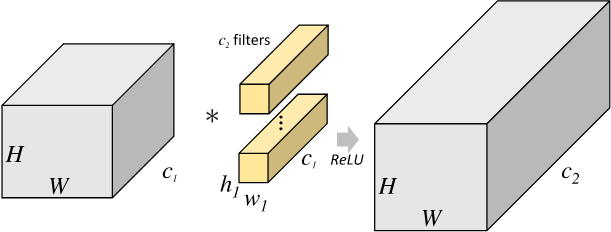
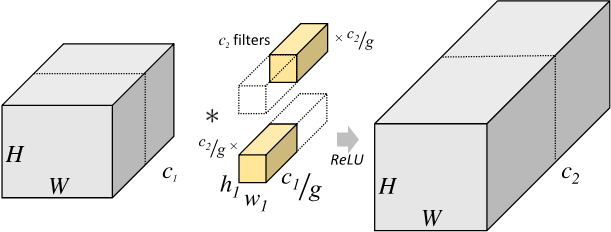
普通卷积核分组卷积

重要的是要注意组的数量必须完美地除以输入通道的数量和输出通道的数量（公约数）。

因此，group conv参数的数量等于没有group参数量除以groups。关于 Pytorch 的计算时间，该算法针对组进行了优化，因此应该减少计算时间。但是，还应该考虑到必须与输出通道的组形成和连接的计算时间相加。

import torch

inputs = torch.randn(32, 2, 7, 7)
model = torch.nn.Conv2d(in_channels=2, out_channels=4, kernel_size=(3, 3), stride=(2, 2), padding=(2,2), dilation=(1,1),
                        groups=2, bias=True)    # 40个参数
outputs = model((inputs))
print(outputs.shape)  # [32, 4, 5, 5]

转置卷积

转置卷积(Transposed Convolution)也称为反卷积（Deconvolution），同时也是一种普通的卷积，最主要的作用就是上采样(upsampling)，相比于邻插值的优点，是能够进行网络学习参数。但是需要注意的是，转置卷积不是卷积的逆运算，它只是恢复到与原来输入feature shape大小相同但数值与原来输入不同的矩阵。

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1)
in_channels：输入通道数

out_channels：输出通道数

kernel_size：卷积核的大小

stride：步幅

padding：零填充将添加到输入中每个维度的两侧。实际填充大小为 dilation * (kernel_size-1)-padding(ConvTranspose)

output_padding：添加到输出形状中每个维度的一侧的附加大小。

groups：分组数

dilation：卷积核元素之间的间距。

输入：$(N, C_{in}, H_{in}, W_{in})$

输出：$(N, C_{out}, H_{out}, W_{out})$

$$H_{out} =(H_{in} −1)×stride[0]−2×P[0]+dilation[0]×(K[0]−1)+output\_padding[0]+1$$

$$W_{out} =(W_{in} −1)×stride[1]−2×P[1]+dilation[1]×(K[1]−1)+output\_padding[1]+1$$

权重：$(C_{in}, \frac{C_{out}}{groups}, K[0], K[1])$

偏置：(C_{out},)

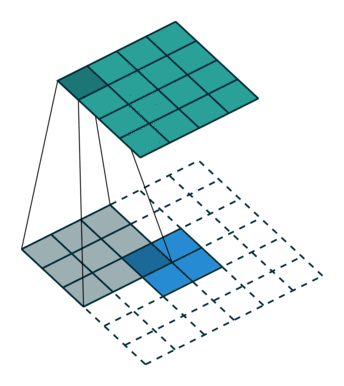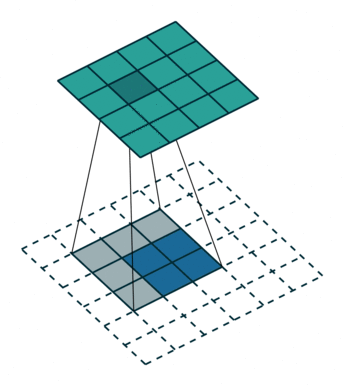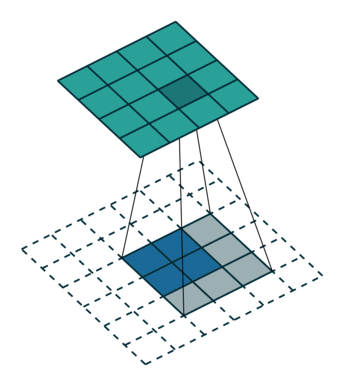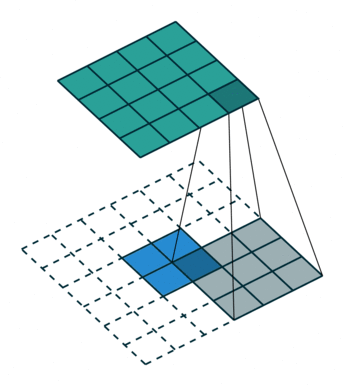
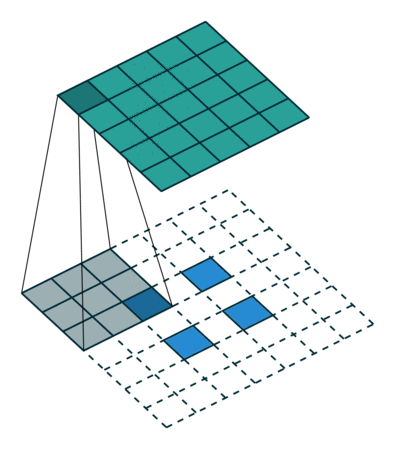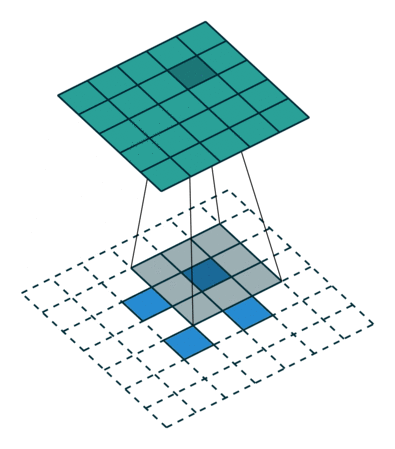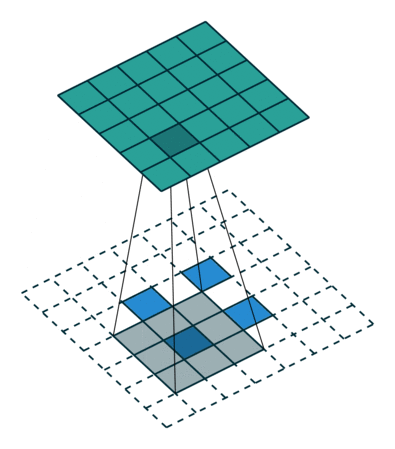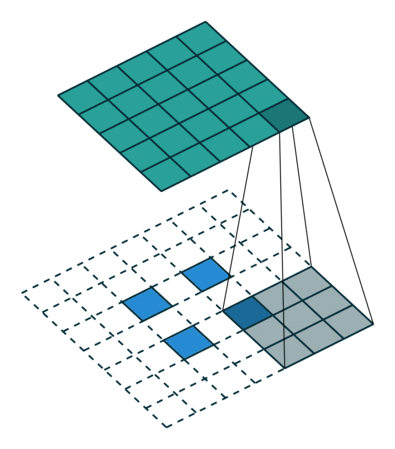
转置卷积运算步骤：

在输入元素间填充s-1 行、列
在输入四周填充dilation*(k-1)行、列
将卷积核参数上下、左右翻转
做正常卷积运算(填充0、步长1)

左图 stride=1，kernel=3，padding=0（实际padding=(k-1)-padding=2）

右图 stride=2，kernel=3，padding=0（实际padding=(k-1)-padding=2）

池化层

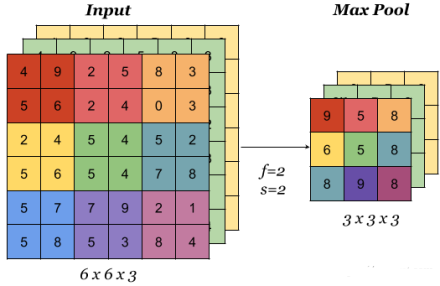
　　池化层用于减小feature map的大小并加快计算速度，以及使其检测到的一些特征更加稳健。

池化的样本类型是max pooling和avg pooling，但现在 max pooling 更为常见。

　　池化层有超参数：size( f )、步幅( s )、类型（最大值或平均值）。但它没有参数；梯度下降没有什么可学的

在多通道输入上完成时，池化会减小高度和宽度（$H_{out}$和$W_{out}$），但保持通道数不变：

池化层有这么几种功能：

它进行了一次特征提取，减小了下一层数据的处理量
这个特征提取，能够有更大的可能性进一步获取更为抽象的信息，防止过拟合，也可以说提高了一定的泛化能力。
能够对输入的微小变化产生更大的容忍。

One-hot编码

　　独热编码(one-hot encoding):使用一个向量的每一个维度来标识一种性质的有无。

$$猫:\begin{pmatrix}1\\ 0\\ 0\\ 0\end{pmatrix}
狗:\begin{pmatrix}0\\ 1\\ 0\\ 0\end{pmatrix}
蛇:\begin{pmatrix}0\\ 0\\ 1\\ 0\end{pmatrix}
猪:\begin{pmatrix}0\\ 0\\ 0\\ 1\end{pmatrix}$$