深度学习中的激活函数
众所周知神经网络单元是由线性单元和非线性单元组成的,一般神经网络的计算时线性的,而非线性单元就是我们今天要介绍的--激活函数,不同的激活函数得出的结果也是不同的。他们也各有各的优缺点,虽然激活函数有自己的发展历史,不断的优化,但是如何在众多激活函数中做出选择依然要看我们所实现深度学习实验的效果。
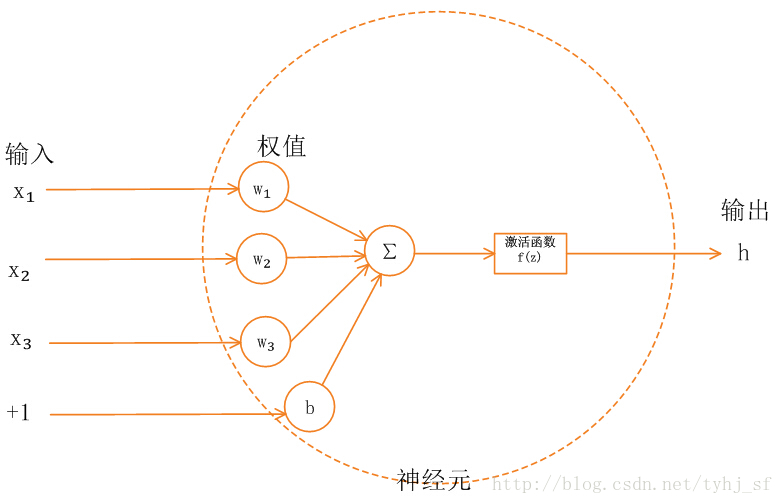
这篇博客会介绍一些常用的激活函数:Sigmoid、tanh、ReLU、LeakyReLU、maxout。以及一些较为冷门的激活函数:PRelu、ELU、SELU
Sigmoid类
sigmoid
sigmoid激活函数将输入$(-\infty ,+\infty)$映射到(0,1)之间,他的数学函数为:
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
 View Code
View Code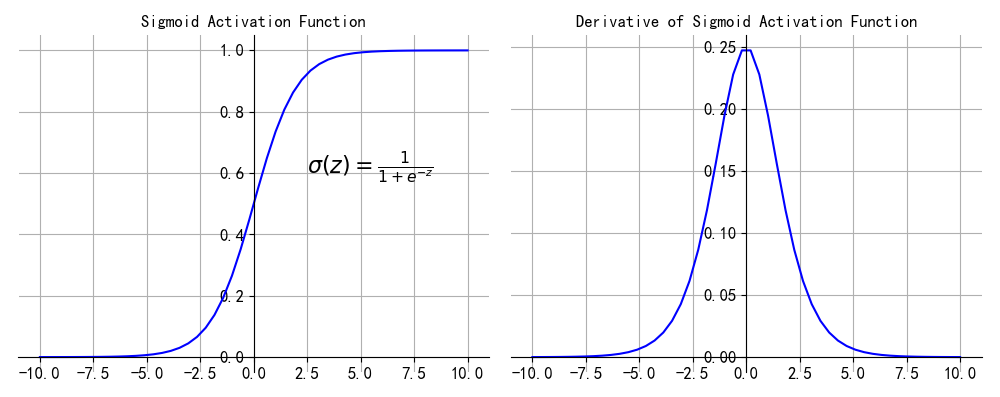
历史上sigmoid非常常用,但是由于他的两个缺点,实际很少用了,现在看到sigmoid激活函数,都是在新手教程中做一些简单的实验。
优点
- 它能够把输入的连续实值变换为0和1之间的输出,适合做概率值的处理。
- 如果是非常大的负数,那么输出就是0
- 如果是非常大的正数,输出就是1
缺点
1、梯度消失
我们从上图可以看出,当x较大或者较小时,sigmoid输出趋近0或1,导数接近0,而后向传递的数学依据是微积分求导的链式法则,当前层的导数需要之前各层导数的乘积,几个小数的相乘,结果会很接近0。Sigmoid导数的最大值是0.25,这意味着导数在每一层至少会被压缩为原来的1/4,通过两层后被变为1/16,…,通过10层后为1/1048576。这种情况就是梯度消失。梯度一旦消失,参数不能沿着loss降低的方向优化,
2、不是以零为中心
通过Sigmoid函数我们可以知道,Sigmoid的输出值恒大于0,输出不是0均值(既zero-centerde),这会导致后一层的神经元将得到上一层输出的非均值的输入。
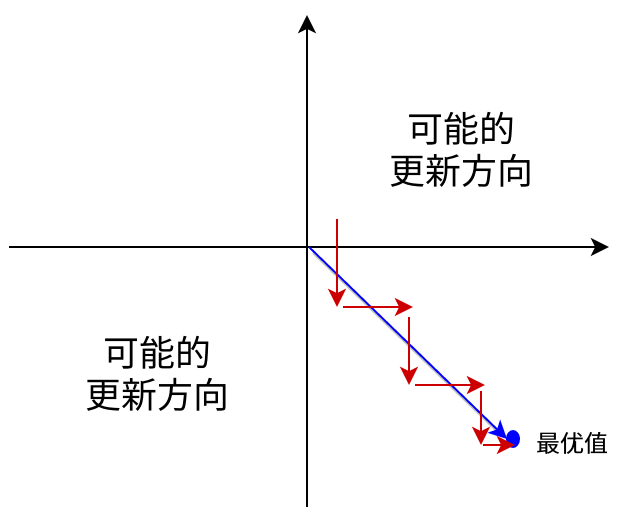
举例来讲$\sigma (\sum_i w_ix_i+b)$,如果$x_i$恒大于0,那么对其$w_i$的导数总是正数或总是负数,向传播的过程中w要么都往正方向更新,要么都往负方向更新,导致有一种捆绑的效果,使得收敛缓慢。且可能导致陷入局部最小值。当然了,如果按batch去训练,那么那个batch可能得到不同的信号,所以这个问题还是可以缓解一下的。
3、运算量大:
解析式中含有幂运算,计算机求解时相对来讲比较耗时。对于规模比较大的深度网络,这会较大地增加训练时间。
Hardsigmoid
$$\operatorname{Hardsigmoid}(x)= \begin{cases}0 & \text { if } x \leq-3, \\ 1 & \text { if } x \geq+3, \\ x / 6+1 / 2 & \text { otherwise }\end{cases}$$
 View Code
View Code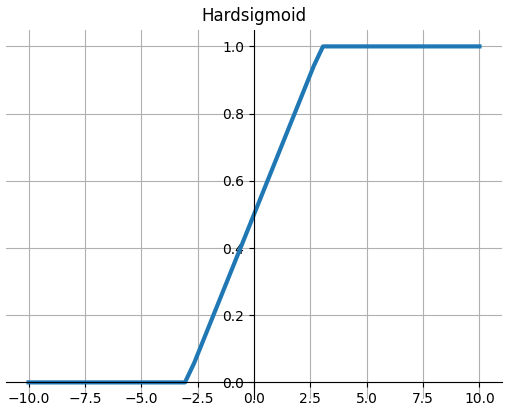
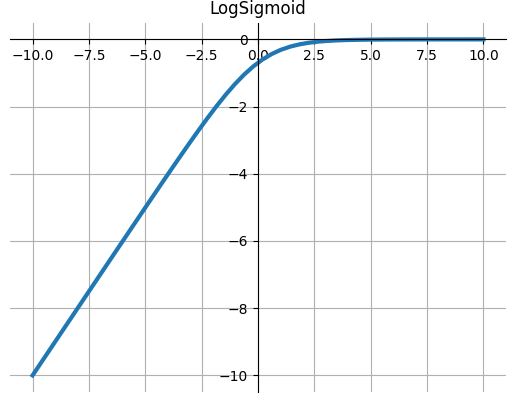
LogSigmoid
$$\operatorname{LogSigmoid}(x)=\log \left(\frac{1}{1+e^{-x}}\right)$$

def LogSigmoid(x): """ torch.nn.LogSigmoid() Applies the element-wise function: """ return np.log(1 / (1 + np.exp(-x)))
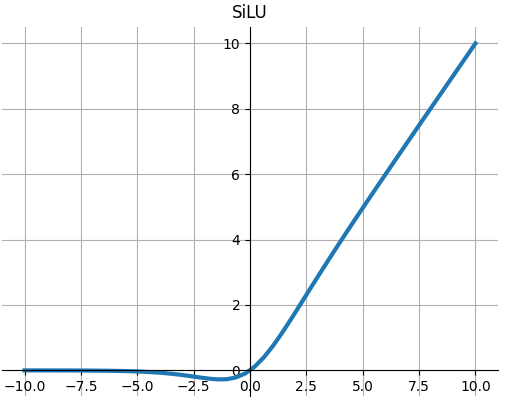
SiLU
$$SiLU(x)=x∗\sigma (x)$$
其中$ \sigma(x)$是sigmoid函数,
请参阅Gaussian Error Linear Units (GELUs) 最初产生的高斯误差线性单元(GELUs),以及Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning 和 Swish: a Self-Gated Activation Function SiLU后来在那里进行了实验。

def SiLU(x): """ torch.nn.SiLU() Sigmoid Linear Unit (SiLU) """ return x * Sigmoid(x)
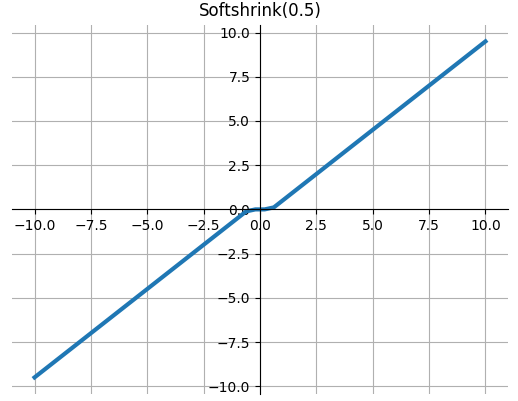
Softshrink
软收缩函数
$$\text { SoftShrinkage }(x)= \begin{cases}x-\lambda, & \text { if } x>\lambda \\ x+\lambda, & \text { if } x<-\lambda \\ 0, & \text { otherwise }\end{cases}$$

def Softshrink(x, lambd=0.5): """ torch.nn.Softshrink() Applies the soft shrinkage function element-wise: """ return np.where(x > lambd, x - lambd, np.where(x < -lambd, x + lambd, 0))
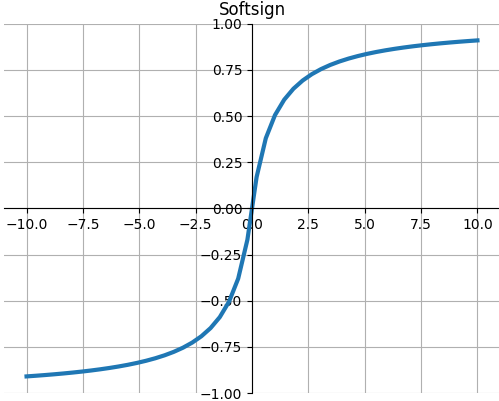
Softsign
$$Softsign(x)=\frac{x}{1+|x|}$$

def Softsign(x): """ torch.nn.Softsign() Applies the element-wise function: """ return x / (1 + np.abs(x))
ReLU类
ReLU
这才是一个目前主流论文中非常常用的激活函数,它的数学公式为:
$$f(x)=max(0,x)$$

def relu(x): return np.where(x<0,0,x)
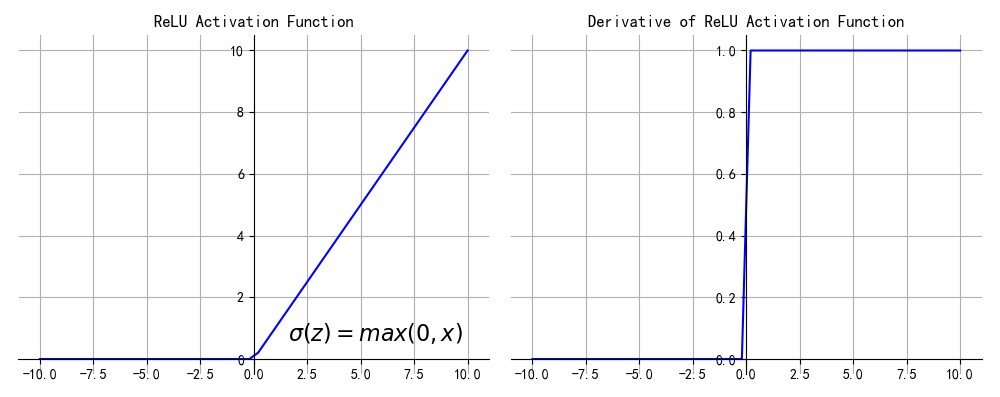
优点
- ReLU的计算量小,收敛速度很快,因为sigmoid和tanh,ReLU有指数运算
- 在正区间(x>0)解决了梯度消失问题。图像数据是在(0~255)之间,即便归一化处理值也大于0,但是音频数据有正有负,不适合relu函数
缺点:
- ReLU的输出不是zero-centered
- RuLU在训练的时候很容易导致神经元“死掉”
死掉:一个非常大的梯度经过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会被任何数据激活相应的权重永远不会更新。有两种原因导致这种情况:1、非常不幸的初始化。2、学习率设置的太高导致在训练过程中参数更新太大,解决方法是使用Xavier初始化方法,合理设置学习率,会降低这种情况的发生概率。或使用Adam等自动调节学习率的算法。
补充:ReLU相比sigmoid和tanh的一个缺点是没有对上界设限,在实际使用中,可以设置一个上限,如ReLU6经验函数: f(x)=min(6,max(0,x))
ReLU6
$$ReLU6(x)=min(max(0,x),6)$$

def ReLU6(x): # return np.min(np.max(x, 0), 6) return np.where(x < 0, 0, np.where(x > 6, 6, x))

LeakyReLU
Leaky ReLU(泄露型线性整流函数),LeakyReLU中的斜率a是自定义的,pReLU中的a是通过训练学习得到的,LeakyReLU是为了解决“ReLU死亡”问题的尝试
$$f(x)=\left\{\begin{matrix}
x&&x>0\\
0.01x&&其他
\end{matrix}\right.$$
ReLU 中当 x<0 时,函数值为 0 。而 Leaky ReLU 则是给出一个很小的负数梯度值,比如 0.01 。
有些研究者的论文指出这个激活函数表现很不错,但是其效果并不是很稳定。

def LeakyReLU(x,a=0.2): return np.where(x < 0, a * x, x)

虽然Leaky ReLU修复了ReLU的神经元死亡问题,但是在实际的使用并没有完全证明Leaky ReLU完全优于ReLU。
PReLU
Parameterised ReLU(PReLU,参数化线性整流函数),在RReLU中,负值的斜率$a_i$在训练中是随机的,$a_i$是可学习的,如果$a_i=0$,那么 PReLU 退化为ReLU;如果$a_i$是一个很小的固定值(如$a_i=0.01$),则 PReLU 退化为 Leaky ReLU。
$a_i$在之后的测试中就变成了固定的了。RReLU的亮点在于,在训练环节中,$a_i$是从一个均匀的分布$U(I,u)$中随机抽取的数值。形式上来说,我们能得到以下数学表达式:
$$f(x)=\left\{\begin{matrix}
x&&x>0\\
a_ix&&x\leqslant 0
\end{matrix}\right.$$
其中$$a_i\sim U(x,y),区间(x,y)上的均匀分布;x,y\in [0,1]$$

def PReLU(x, a): return np.where(x < 0, a * x, x)
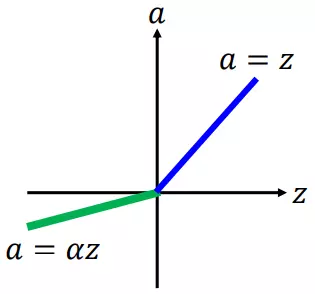
优点
(1)PReLU只增加了极少量的参数,也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的,当不同channels使用相同的$a$时,参数就更少了。
(2)BP更新$a$时,采用的是带动量的更新方式,如下:
$$\Delta a_i=\mu \Delta a_i+\epsilon \frac{\partial \varepsilon }{\partial a_i}$$
RReLU
$$\operatorname{RReLU}(x)= \begin{cases}x & \text { if } x \geq 0 \\ a x & \text { otherwise }\end{cases}$$
from paper: Empirical Evaluation of Rectified Activations in Convolutional Network.

def RReLU(x, lower=1. / 8, upper=1. / 3): """ torch.nn.RReLU() Applies the randomized leaky rectified liner unit element-wise, which randomly chooses in-place an element of the input tensor and computes the output using the formula: """ return np.where(x < 0, np.random.uniform(lower, upper) * x, x)
其中$\alpha$是是从均匀分布$U(lower, upper)$中随机抽样的,在训练期间,而在评估期间,$a=\frac{lower+upper}{2}$

ELU
Exponential Linear Unit(ELU,指数化线性单元),为了解决ReLU存在的问题而提出的,ELU有ReLU的基本所有优点,以及不会有Dead ReLU问题,和输出的均值接近0(zero-certered),它的一个小问题在于计算量稍大。类似于Leaky ReLU,理论上虽然好于ReLU,但在实际使用中目前并没有好的证据ELU总是优于ReLU。
from paper: Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)
$$f(x)=\left\{\begin{matrix}
x&&x>0\\
\alpha (e^x-1)&&x\leq 0
\end{matrix}\right.$$
$$f'(x)=\left\{\begin{matrix}
1&&x>0\\
f(x)+a&&x\leq 0
\end{matrix}\right.$$

def elu(x, a): return np.where(x < 0, a*(np.exp(x)-1), a*x)

其中$\alpha$是一个可调整的参数,它控制着ELU负值部分在何时饱和。右侧线性部分使得ELU能够缓解梯度消失,而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零,所以收敛速度更快
SELU
$$SELU(x)=\lambda \left\{\begin{matrix}
x&&x>0\\
\alpha e^x-\alpha &&x\leq 0
\end{matrix}\right.$$
经过该激活函数后使得样本分布自动归一化到0均值和单位方差(自归一化,保证训练过程中梯度不会爆炸或消失,效果比Batch Normalization 要好)
其实就是ELU乘了个$\alpha$,关键在于这个$\alpha$是大于1的。以前relu,prelu,elu这些激活函数,都是在负半轴坡度平缓,这样在激活函数的方差过大的时候可以让它减小,防止了梯度爆炸,但是正半轴坡度简单的设成了1。而selu的正半轴大于1,在方差过小的的时候可以让它增大,同时防止了梯度消失。这样激活函数就有一个不动点,网络深了以后每一层的输出都是均值为0方差为1。

def SELU(x): """ torch.nn.SELU() paper: Self-Normalizing Neural Networks . """ alpha = 1.6732632423543772848170429916717 scale = 1.0507009873554804934193349852946 return scale * np.where(x > 0, x, alpha * (np.exp(x) - 1))

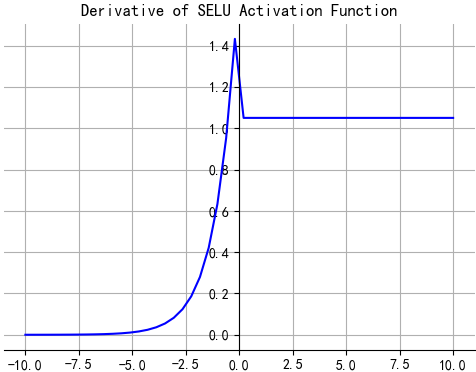
其中超参$\alpha$和$\lambda$的值是 证明得到 的(而非训练学习得到):
$\alpha$= 1.6732632423543772848170429916717
$\lambda$= 1.0507009873554804934193349852946
即:
- 不存在死区
- 存在饱和区(负无穷时, 趋于$-\alpha \lambda$)
- 输入大于零时,激活输出对输入进行了放大
CELU
$$f(x)=\left\{\begin{matrix}
x&&x>0\\
\alpha (e^{x/a}-1)&&x\leq 0
\end{matrix}\right.$$
from paper :Continuously Differentiable Exponential Linear Units .

def CELU(x, alpha=1.0): """ torch.nn.CELU() paper: Continuously Differentiable Exponential Linear Units """ # return np.max(0, x) + np.min(0, alpha * (np.exp(x / alpha) - 1)) return np.where(x > 0, x, 0) + np.where(alpha * (np.exp(x / alpha) - 1) < 0, alpha * (np.exp(x / alpha) - 1), 0)
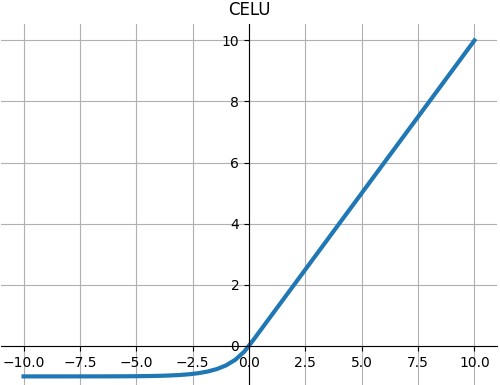
GLU
应用门控线性单位函数$GLU(a,b)=a\otimes \sigma (b)$,其中$a$是输入矩阵的前半部分,$b$是下半部分。

def GLU(x, dim=-1): """ torch.nn.GLU() paper: Language Modeling with Gated Convolutional Networks """ return x[:, :x.shape[dim] // 2] * Sigmoid(x[:, x.shape[dim] // 2:])
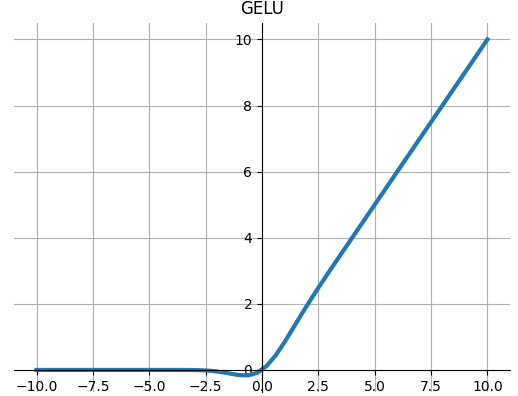
GELU
应用高斯误差线性单位函数:
$$GELU(x)=x*\Phi (x)$$
其中$\Phi (x)$是高斯分布的累积分布函数。
当近似参数为tanh时,Gelu的估计为
$$GELU(x)=0.5*x*(1+Tanh(\sqrt{2/\pi}*(x+0.044715*x^3)))$$

def GELU(x): """ torch.nn.GELU() paper: Gaussian Error Linear Units (GELUs) """ return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3))))
Softplus
$$Softplus(x)= \frac{1}{\beta}∗log(1+e^{\beta∗x})) $$
SoftPlus是一个光滑的近似于ReLU函数,可以使用 约束一台机器的输出总是正的。为了数值稳定性,当$input>\beta>threshold$时 实现恢复到线性函数 。
 View Code
View Code
Mish
$$Mish(x)=x∗Tanh(Softplus(x))$$
from paper:Mish: A Self Regularized Non-Monotonic Neural Activation Function
 View Code
View Code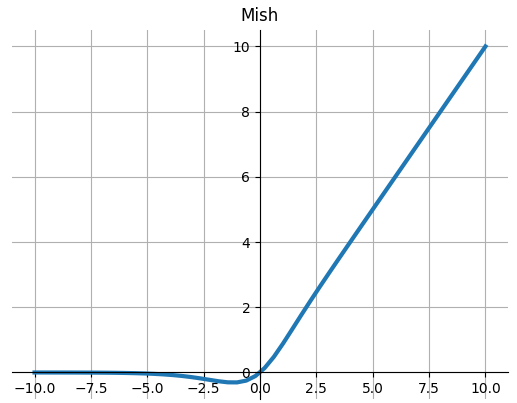
Hardswish
$$Hardswish(x)=\left\{\begin{matrix}
0 &x>-3\\
x &x<+3\\
x(x+3)/6&otherwise
\end{matrix}\right.$$
from paper: Searching for MobileNetV3.
 View Code
View Code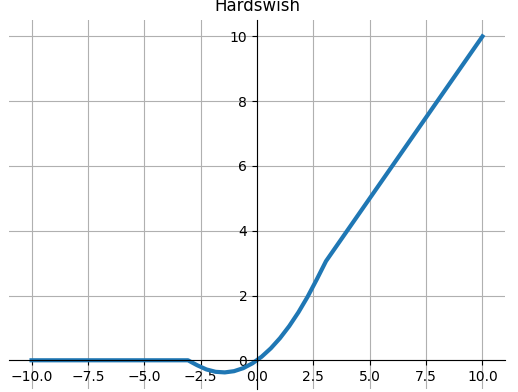
Swish
Swish 激活函数,该函数又叫作自门控激活函数,它近期由谷歌的研究者发布,数学公式为:
$$\sigma (x)=\frac{x}{1+e^{-x}}$$
根据论文(https://arxiv.org/abs/1710.05941v1),Swish 激活函数的性能优于 ReLU 函数。

根据上图,我们可以观察到在 x 轴的负区域曲线的形状与 ReLU 激活函数不同,因此,Swish 激活函数的输出可能下降,即使在输入值增大的情况下。大多数激活函数是单调的,即输入值增大的情况下,输出值不可能下降。而 Swish 函数为 0 时具备单侧有界(one-sided boundedness)的特性,它是平滑、非单调的。更改一行代码再来查看它的性能,似乎也挺有意思。
Tanh类
Tanh
Tanh 激活函数又叫作双曲正切激活函数(hyperbolic tangent activation function)。与 Sigmoid 函数类似,但 Tanh 函数将其压缩至-1 到 1 的区间内,输出是zero-centered的(零为中心),在实践中,Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值,零输入值的映射接近零,正数输入被当作正值。
数学函数为:
$$f(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^z}+e^{-z}$$
 View Code
View Code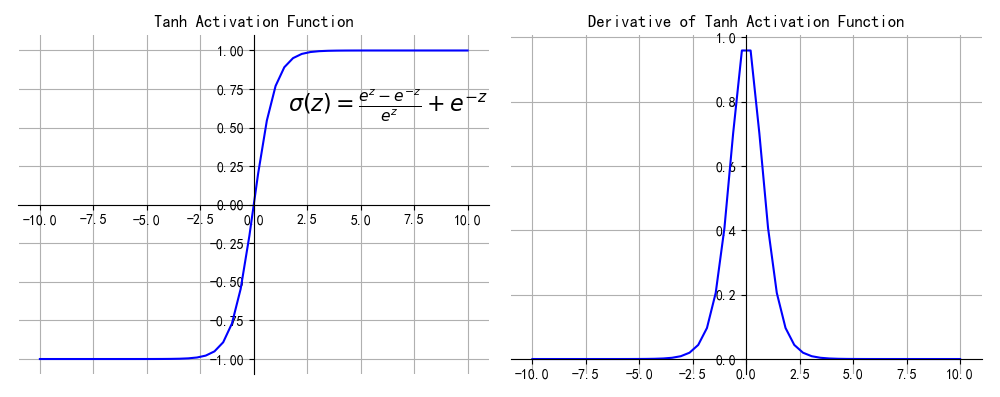
优点
- sigmoid的优点他都有,另外 tanh的输出是zero-centered,以0为中心
缺点
1、特殊情况存在梯度消失问题
当输入值过大或者过小,提取趋近于0,失去敏感性,处于饱和状态。
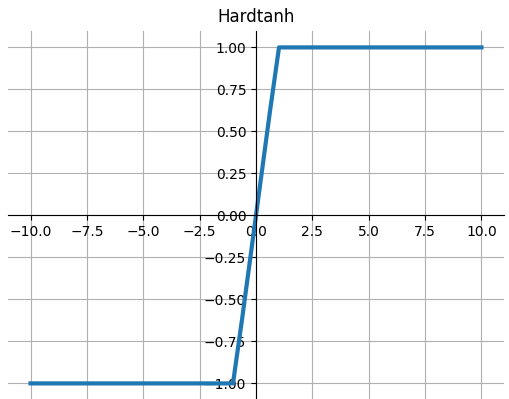
Hardtanh
$$HardTanh(x)=\left\{\begin{matrix}
max\_val &x>max_val\\
min\_val &x<min_val\\
x&otherwise
\end{matrix}\right.$$

def Hardtanh(x, min_val=-1., max_val=1.): """ torch.nn.Hardtanh() Applies the HardTanh function element-wise. """ return np.where(x < min_val, min_val, np.where(x > max_val, max_val, x))
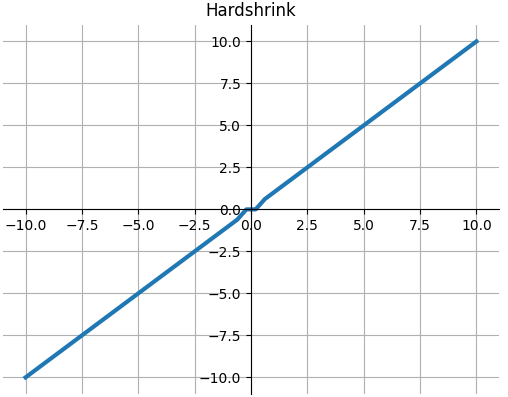
Hardshrink
$$Hardshrink(x)=\left\{\begin{matrix}
x &x>\lambda\\
x &x<-\lambda\\
0&otherwise
\end{matrix}\right.$$

def Hardshrink(x, lambd=0.5): """ torch.nn.Hardshrink(lambd=0.5) Applies the Hard Shrinkage (Hardshrink) function element-wise. """ return np.where(x > lambd, x, np.where(x < -lambd, x, 0))
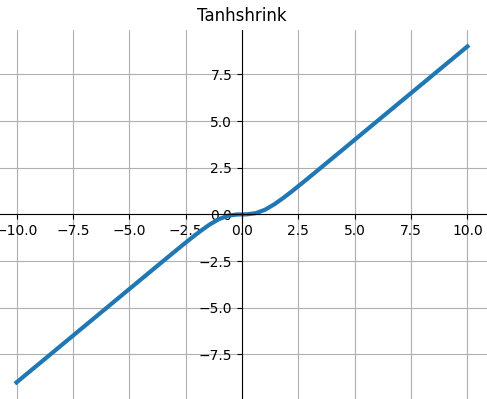
Tanhshrink
$$Tanhshrink(x)=x−tanh(x)$$

def Tanhshrink(x): """ torch.nn.Tanhshrink() """ return x - Tanh(x)
Threshold
$$Threshold(x)=\left\{\begin{matrix}
x &x>threshold\\
value &otherwise
\end{matrix}\right.$$

def Threshold(x, threshold, value): """ torch.nn.Threshold() Applies the thresholding function element-wise: """ return np.where(x > threshold, x, value)
SoftMax
在数学Softmax函数,或称归一化指数函数。它将一个含任意实数的K维向量z “压缩”到另一个K维实向量$\sigma _(z)$中,使得每个元素的范围都在(0,1)之间,并且所有元素的和为1,该函数的形式通常按下面的式子给出:
$$\sigma _i(z)=\frac{e^{z_i}}{\sum_{k=1}^{K}e^{z_k}},k=1,...,K$$
其中$\sum \sigma_i(z)=1$。oftmax通常在神经网络的最后一层作为分类器的输出,把神经元中线性部分输出的得分值(score),转换为概率值。softmax输出的是(归一化)概率,输出值(概率)最大的即为分类结果。
z = np.array([1.0, 2.0, 3.0, 4.0, 1.0]) print(np.exp(z)/sum(np.exp(z))) # [0.03106277 0.08443737 0.22952458 0.6239125 0.03106277]
一般用softmax激活函数的都会用交叉熵损失函数,说交叉熵之前先介绍相对熵,相对熵又称为KL散度(Kullback-Leibler Divergence),用来衡量两个分布之间的距离,记为$D_{KL}(p||q)$
$$\begin{align} D_{KL}(p||q)=&\sum_x p(x)\log \frac{p(x)}{q(x)}\\
=&\sum_xp(x)\log p(x)-\sum_xp(x)\log q(x)\\
=&-H(p)-\sum_xp(x)\log q(x)
\end{align}$$
这里$H(p)是p的熵$。
假设有两个分布$p$和$q$,他们在给定样本集上的交叉熵定义为:
$$CE(p,q)=-\sum_xp(x)\log q(x)=H(p)+D_{KL}(p||q)$$
从这里可以看出,交叉熵和相对熵相差了$H(p)$,而当$p$已知的时候,$H(p)$是个常数,所以交叉熵和相对熵在这里是等价的,反映了分布$p$和$q$之间的相似程度。交叉熵所描述的是经过训练分类结果的信息熵和测试集分类结果的信息熵之间的差距。在拟合过程中产生的熵是有差距的,这个差距由交叉熵来定义。那么只要熵差越小,就越接近真实值。
pytorch的F.cross_entropy()包含了softmax函数,所以写代码的时候可以不用写softmax,对PyTorch中F.cross_entropy()函数的理解
如何选择合适的激活函数
这个问题目前没有确定的方法,凭一些经验吧。
1)深度学习往往需要大量时间来处理大量数据,模型的收敛速度是尤为重要的。所以,总体上来讲,训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
2)如果使用 ReLU,那么一定要小心设置 learning rate,而且要注意不要让网络出现很多 “dead” 神经元,如果这个问题不好解决,那么可以试试 Leaky ReLU、PReLU。
3)最好不要用 sigmoid,你可以试试 tanh,不过可以预期它的效果会比不上 ReLU 和 Maxout.
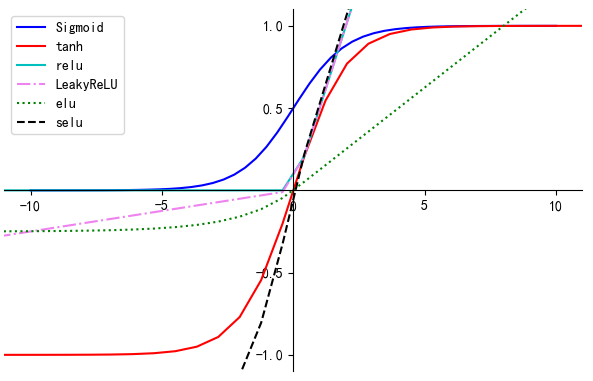
最后来一张全家照

# -*- coding:utf-8 -*- # Author:凌逆战 | Never # Date: 2022/9/27 """ 激活函数全家照 """ import numpy as np import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示符号 def sigmoid(x): return 1.0 / (1.0 + np.exp(-x)) def tanh(x): return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)) def relu(x): return np.where(x < 0, 0, x) def prelu(x, a): return np.where(x < 0, a * x, x) def elu(x, a): return np.where(x < 0, a * (np.exp(x) - 1), a * x) def selu(x): alpha = 1.6732632423543772848170429916717 scale = 1.0507009873554804934193349852946 return scale * np.where(x >= 0.0, x, alpha * (np.exp(x) - 1)) fig = plt.figure(figsize=(6, 4)) x = np.linspace(-10, 10) y_sigmoid = sigmoid(x) y_tanh = tanh(x) y_relu = relu(x) y_LeakyReLU = prelu(x, 0.05) y_elu = elu(x, 0.25) y_selu = selu(x) # 截取x,y的某一部分 plt.xlim(-11, 11) plt.ylim(-1.1, 1.1) ax = plt.gca() # 获取当前坐标的位置 # 去掉坐标图的上和右 spine翻译成脊梁 ax.spines['top'].set_color('none') ax.spines['right'].set_color('none') # 指定坐标的位置 ax.xaxis.set_ticks_position('bottom') # 设置bottom为x轴 ax.yaxis.set_ticks_position('left') # 设置left为y轴 ax.spines['bottom'].set_position(('data', 0)) # 这个位置的括号要注意 ax.spines['left'].set_position(('data', 0)) ax.set_xticks([-10, -5, 0, 5, 10]) # X轴显示的刻度 ax.set_yticks([-1, -0.5, 0.5, 1]) # Y轴显示的刻度 plt.plot(x, y_sigmoid, label="Sigmoid", color="blue") # 蓝色 plt.plot(2 * x, y_tanh, label="tanh", color="red") # 红色 plt.plot(2 * x, y_relu, label="relu", color="c") # 青色 plt.plot(2 * x, y_LeakyReLU, '-.', label="LeakyReLU", color="Violet") # 紫色 plt.plot(2 * x, y_elu, ":", label="elu", color="green") # 绿色 plt.plot(2 * x, y_selu, "--", label="selu", color="k") # 黑色 plt.legend() plt.show()
参考文献
SELU论文地址:【Self-Normalizing Neural Networks】.
StevenSun2014的CSDN博客:常用激活函数总结
26种神经网络激活函数可视化(留着以后看,原文更加精彩)
【python学习乐园】SciPy求函数的导数
【paperwithcode】Activation Functions


 浙公网安备 33010602011771号
浙公网安备 33010602011771号