Transformer模型详解
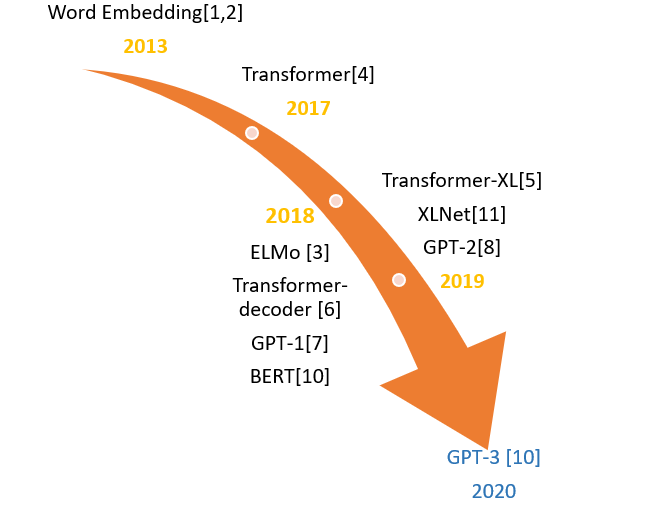
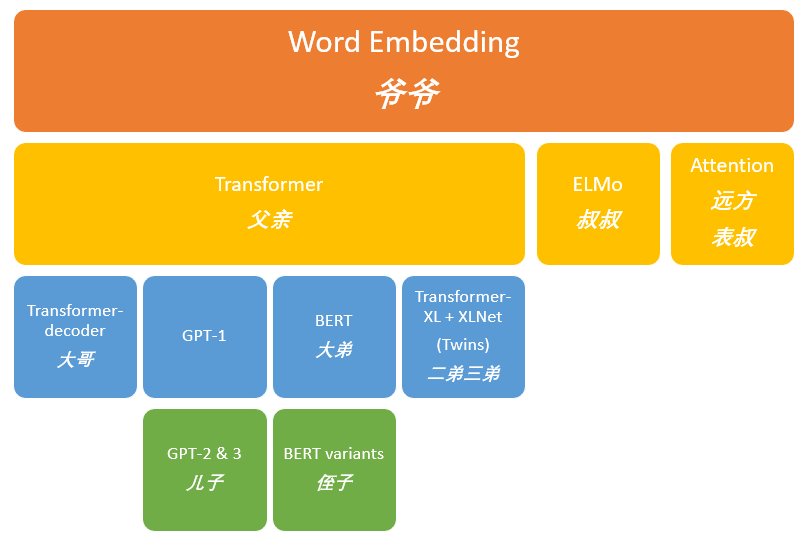
2013年----word Embedding
2017年----Transformer
2018年----ELMo、Transformer-decoder、GPT-1、BERT
2019年----Transformer-XL、XLNet、GPT-2
2020年----GPT-3
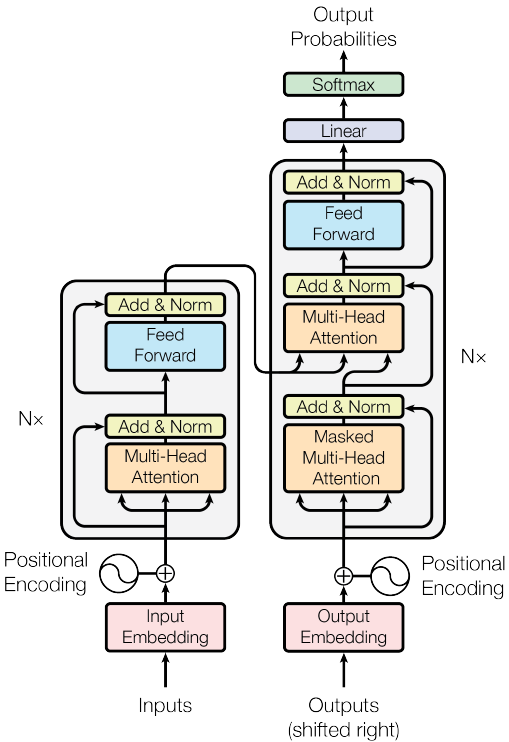
Transformer
谷歌提出的Transformer模型,用全Attention的结构代替的LSTM,在翻译上取得了更好的成绩。这里基于Attention Is All You Need(code:https://github.com/hyunwoongko/transformer),对 Transformer 做一个介绍。模型结构如下图所示,模型包含 encoder 和 decoder 两部分,其中 encoder 包含 N个(6个)当前单元,decoder 部分包含 N个框中单元。下面我们分块对其进行描述。
Position Embedding
Encoder 的输入包含词向量和位置向量(Position Embedding),词向量 部分和正常的网络一样,通过学习获得,维度为$d_{model}$。位置向量 将每个位置编号,然后每个编号对应一个向量,通过结合位置向量和词向量,就给每个词都引入了一定的位置信息,这样Attention就可以分辨出不同位置的词了。而位置向量则和以往不同,以往的位置向量是通过学习获得的,而这里谷歌提出了一种位置向量嵌入的方法:
$$\left\{\begin{array}{l}
P E_{2 i}(p)=\sin \left(p / 10000^{2 i / d_{p o s}}\right) \\
P E_{2 i+1}(p)=\cos \left(p / 10000^{2 i / d_{p o s}}\right)
\end{array}\right.$$
这里的意思是将id为$p$的位置映射为一个$d_{pos}$维的位置向量,这个向量的第$i$个元素的数值就是$PE_i(p)$。Google在论文中说到他们比较过直接训练出来的位置向量和上述公式计算出来的位置向量,效果是接近的。因此显然我们更乐意使用公式构造的Position Embedding了,我们称之为Sinusoidal形式的Position Embedding。
Position Embedding本身是一个绝对位置的信息,但在语言中,相对位置也很重要,Google选择前述的位置向量公式的一个重要原因是:由于我们有$sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta $以及$cos(\alpha +\beta )=cos\alpha cos\beta −sin\alpha sin\beta $,这表明位置$p+k$的向量可以表示成位置$p$的向量的线性变换,这提供了表达相对位置信息的可能性。
Encoder部分
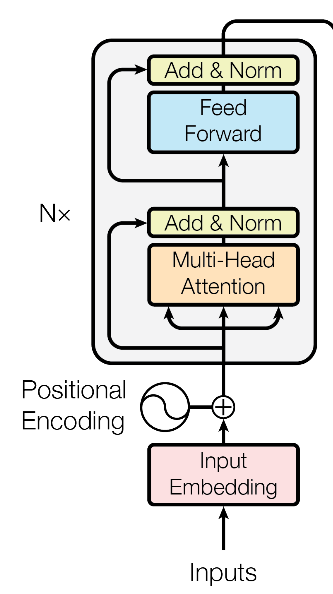
Encoder 部分由6个相同的子模块组成,每个子模块就是上面图中左侧那个方块了。包含几个子部分:
- Multi-Head Attention
- Residual connection
- Normalisation
- Position-wise Feed-Forward Networks
在Encoder 内部又可以看做包含两个子层,一个是 Multi-Head Self-Attention为主,另一个是 Position-wise Feed-Forward Networks,每个子层内的运算可以总结为:
$$sub\_layer\_output = LayerNorm(x + (SubLayer(x)))$$
接下来着重介绍 两个子层。Multi-Head Self-Attention由 Scaled Dot-product Attention 和 Multi-Head Attention 以及 Self Attention 组成,下面依次进行讲解。
Scaled Dot-Product Attention
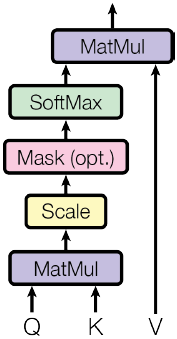
$$Attention(Q,\ K,\ V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$$
其中$Q,K,V$分别是query、key、value,他们的shape分别为$(n×d_k)、(m×d_k)、(m×d_v)$。这个公式相比于正常的Dot Attention多了一个缩放因子$\frac{1}{\sqrt{d_k}}$,这个缩放因子可以防止内积过大,防止它经过 softmax 后落入饱和区间,因为饱和区的梯度几乎为0,容易发生梯度消失。如果忽略激活函数softmax的话,那么事实上它就是$Q,K,V$三个矩阵相乘,最后的结果是一个$n×d_v$的矩阵。于是我们可以认为:这是一个Attention层,将序列$Q$编码成了一个新的$n×d_v$的序列。我们可以理解为:Q通过与K内积并sofrmax的方式,来得到Q与V的相似度。
在这个 scaled dot-product attention 中,还有一个 mask部分,在训练时它将被关闭,在测试或者推理时,它将被打开去遮蔽当前预测词后面的序列。
事实上这种Attention的定义并不新鲜,但由于Google的影响力,我们可以认为现在是更加正式地提出了这个定义,并将其视为一个层来看待;此外这个定义只是注意力的一种形式,还有一些其他选择,比如$query$跟$key$的运算方式不一定是点乘(还可以是拼接后再内积一个参数向量),甚至权重都不一定要归一化,等等。

class ScaleDotProductAttention(nn.Module): """compute scale dot product attention Query : given sentence that we focused on (decoder) Key : every sentence to check relationship with Qeury(encoder) Value : every sentence same with Key (encoder) """ def __init__(self): super(ScaleDotProductAttention, self).__init__() self.softmax = nn.Softmax(dim=-1) def forward(self, query, key, value, mask=None): """ :param query: [b_size, n_heads, length, d_k] :param key: [b_size, n_heads, length, d_k] :param value: [b_size, n_heads, length, d_v] :param mask: :return: """ batch_size, head, length, dk = key.size() # 1. dot product Query with Key^T to compute similarity score = torch.matmul(query, key.transpose(2, 3)) / math.sqrt(dk) # scaled dot product # 2. apply masking (opt) if mask is not None: score = score.masked_fill(mask == 0, -10000) # 3. pass them softmax to make [0, 1] range attention = self.softmax(score) # 4. multiply with Value out = torch.matmul(attention, value) return out, attention
Multi-Head Attention
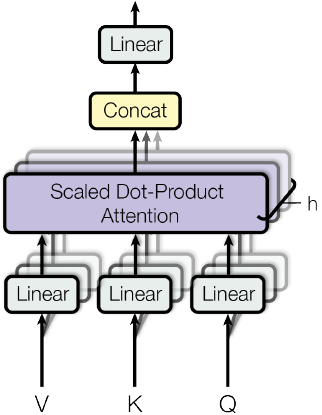
Multi-Head Attention就是把$Q,K,V$通过参数矩阵映射一下,然后再做Attention,把这个过程重复做$h$次,结果拼接起来。具体来说
$$\begin{equation}head_i = Attention({Q}{W}_i^Q,{K}{W}_i^K,{V}{W}_i^V)\end{equation}$$
其中$W_i^Q、W_i^K、W_i^V$的shape分别为$(d_k\times \tilde{d}_k)、(d_k\times \tilde{d}_k)、(d_v\times \tilde{d}_v)$,然后
$$\begin{equation}MultiHead({Q},{K},{V}) = Concat(head_1,...,head_h)\end{equation}$$
最后得到一个$n\times (h\tilde{d}_v)$的序列,所谓Multi-Head(多头),就是只多做几次同样的事情(参数不共享),然后把结果拼接。其中需要注意的是,一方面不同的head的矩阵是不同的,另一方面multi-head-Attention可以并行计算,论文里$h=8,d_k=d_v=d_{model}/4=64$
一般来说一个多头 attention 的效果要优于单个 attention。按照谷歌官方的说法,这么做形成多个子空间,可以让模型关注不同方面的信息,体现出差异性。但有实验表明,头之间的差距随着所在层数变大而减小,因此这种差异性是否是模型追求的还不一定。
至于头数 h 的设置,并不是越大越好,到了某一个数就没效果了。

class MultiHeadAttention(nn.Module): def __init__(self, d_model, n_head): super(MultiHeadAttention, self).__init__() self.n_head = n_head self.attention = ScaleDotProductAttention() self.linear_q = nn.Linear(d_model, d_model) self.linear_k = nn.Linear(d_model, d_model) self.linear_v = nn.Linear(d_model, d_model) self.linear_o = nn.Linear(d_model, d_model) def forward(self, query, key, value, mask=None): # 1. dot product with weight matrices query, key, value = self.linear_q(query), self.linear_k(key), self.linear_v(value) # 2. split tensor by number of heads query, key, value = self.split(query), self.split(key), self.split(value) # 3. do scale dot product to compute similarity out, attention = self.attention(query, key, value, mask=mask) # 4. concat and pass to linear layer out = self.concat(out) out = self.linear_o(out) return out def split(self, tensor): """ split tensor by number of head :param tensor: [batch_size, length, d_model] :return: [batch_size, head, length, d_tensor] """ batch_size, length, d_model = tensor.size() d_tensor = d_model // self.n_head tensor = tensor.view(batch_size, length, self.n_head, d_tensor).transpose(1, 2) # it is similar with group convolution (split by number of heads) return tensor def concat(self, tensor): """ inverse function of self.split(tensor : torch.Tensor) :param tensor: [batch_size, head, length, d_tensor] :return: [batch_size, length, d_model] """ batch_size, head, length, d_tensor = tensor.size() d_model = head * d_tensor tensor = tensor.transpose(1, 2).contiguous().view(batch_size, length, d_model) return tensor
Self Attention
在Google的论文中,大部分的Attention都是Self Attention,即“自注意力”,或者叫内部注意力。也就是说,在序列内部做Attention,寻找序列内部的联系。体现在公式上就是$Attention(X,X,X)$,$X$是输入序列。内部注意力在机器翻译(甚至是一般的Seq2Seq任务)的序列编码上是相当重要的,而之前关于Seq2Seq的研究基本都只是把注意力机制用在解码端。
当然,更准确来说,Google所用的是Self Multi-Head Attention:
$$\begin{equation}{Y}=MultiHead({X},{X},{X})\end{equation}$$
Position-wise Feed-Forward Networks
论文里说,它是一个前馈全连接网络,它被等同的应用到每一个位置上(applied to each position separately and identically),它由两个线性变换和ReLU激活函数组成:
$$FFN(x)=max(0,xW_1+b_1)W_2+b_2$$
这个线性变换被应用到各个位置上,并且它们的参数是相同的。不过不同层之间的参数就不同了。这相当于一个核大小为1 的卷积。
一个注意的地方是,$W_1$的维度是(2048,512),$W_2$是 (512,2048)。 即先升维,后降维,这是为了扩充中间层的表示能力,从而抵抗 ReLU 带来的模型表达能力的下降。

class PositionwiseFeedForward(nn.Module): def __init__(self, d_model, hidden, drop_prob=0.1): super(PositionwiseFeedForward, self).__init__() self.linear1 = nn.Linear(d_model, hidden) self.linear2 = nn.Linear(hidden, d_model) self.relu = nn.ReLU() self.dropout = nn.Dropout(p=drop_prob) def forward(self, x): x = self.linear1(x) x = self.relu(x) x = self.dropout(x) x = self.linear2(x) return x
Decoder部分
Decoder 部分相比于 Encoder ,结构上多了一个 Masked Multi-Head Attention 子层,它对decoder 端的序列做 attention。相比于正常的 Scaled Dot-Product Attention,它在 Scale 后加了一个Mask 操作。这是因为在解码时并不是一下子出来的,它还是像传统 decoder 那样,一个时间步一个时间步的生成,因此在生成当前时间步的时候,我们看不到后面的东西,因此用 MASK 给后面的 遮住。
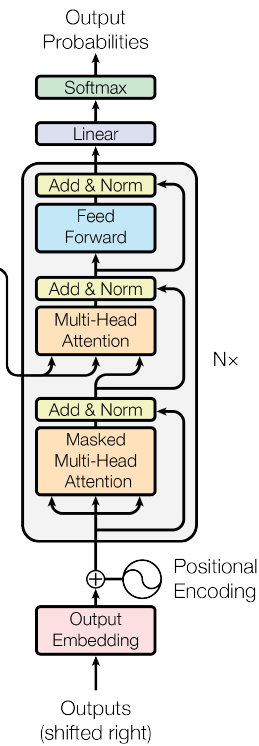
因此在解码时的流程为:
- 假设当前已经解码的序列为$s1,s2,…,st−1$,把该序列做词向量和位置向量嵌入
- 对上述向量做 Masked Multi-Head Attention,把得到的结果作为 Q
- Encoder 端的输出向量看做 K,V
- 结合 Q,K,V 做 Multi-Head Attention 和 FFN等操作
- 重复 decoder 部分 的子结构得到输出,而后解码得到输出词的概率
Attention的原理
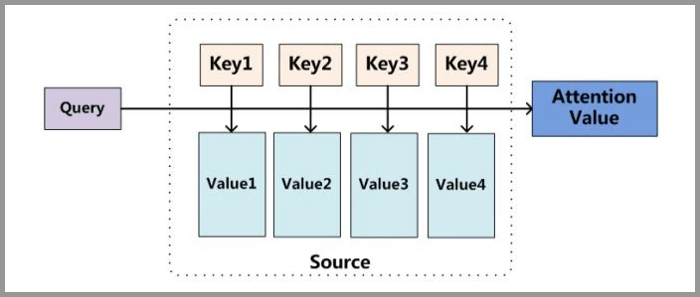
我罗列了两种理解方式,个人还是喜欢第一种,直接了当的,
直接解释:Source里面有很多value,为了方便查找,我们给每个value都标记一个key,当我们想要了解query的时候,就可以通过key去查找相关的value了。
案例解释:图书馆(source)里面有很多书(value),为了方便查找,我们给书做了编号(key),当我们想要了解漫威(query)的时候,我们就可以看看那些动漫、电影、甚至二战相关的书籍。
如果做阅读理解的话,Q可以是篇章的向量序列,取K=V为问题的向量序列,那么输出就是所谓的Aligned Question Embedding。
Attention原理的3步分解
第一步:query和key进行相似度计算,得到权值
第二步:将权值进行归一化,得到直接可用的权值
第三步:将权值和value进行加权求和
从上面的建模,我们可以大致感受到Attention的思路简单,四个字“带权求和”就可以高度概括,大道至简。
Attention的N中类型
下面从模型结构、计算区域、所用信息、使用模型等方面对Attention的形式进行归类,如下图所示
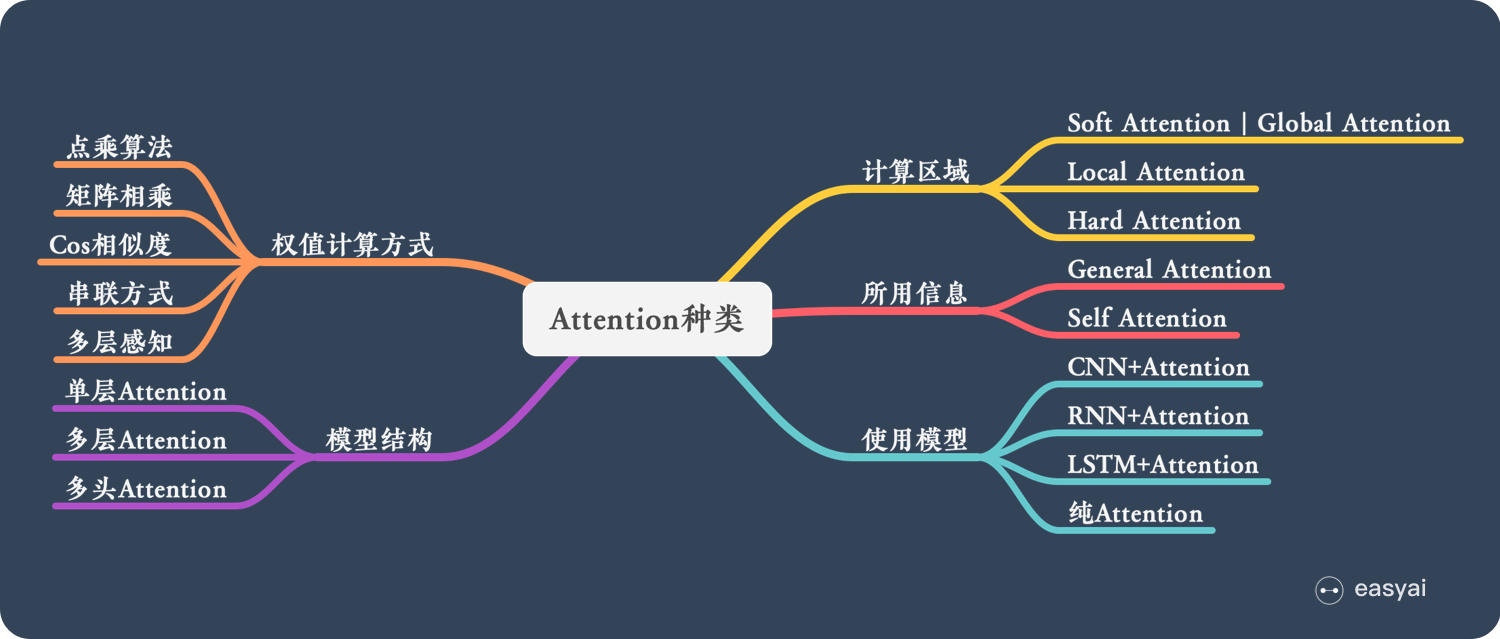
计算区域
根据Attention的计算区域,可以分成以下几种:
Soft Attention:这是比较常见的Attention方式,对所有key求权重概率,每个key都有对应的权重,是一种全局的计算方式(也可以叫做Global Attention)。这种方式比较理想,参考了所有key的内容,再进行加权。但是计算量可能会比较大一些。
Hard Attention:这种方式是直接精准定位到某个key,其余key就都不管了,相当于这个key的概率是1,其余key的概率全部都是0。因此这种对齐方式要求很高,要求一步到位,如果没有正确对齐,会带来很大的影响。另一方面,因为不可导,一般需要用强化学习的方法进行训练(或者使用gumbel softmax子类的)。
Local Attention:这种方式其实是以上两种方式的一个折中,对一个窗口区域进行计算。先用Hard方式定位到某个地方,以这个点为中心可以得到一个窗口区域,在这个小区域内用Soft方式来算Attention。
结构层次
单层Attention:用一个query对一段原文进行一次attention
多层Attention:一般用于文本具有层次关系的模型,假设我们把一个document划分成多个句子,在第一层,我们分别对每个句子使用attention计算出一个句向量(也就是单层attention);在第二层,我们对所有句向量再做attention计算出一个文档向量(也是一个单层attention),最后再用这个文档向量去做任务。
多头Attention:这是Attention is All You Need中提到的multi-head attention,用到了多个query对一段原文进行了多次attention,每个query都关注到原文的不同部分,相当于重复做多次单层attention
使用模型
从模型上看,Attention一般用在CNN和LSTM上,也可以直接进行纯Attention计算。
CNN+Attention:CNN的卷积操作可以提取重要特征,我觉得这也算是Attention的思想,但是CNN的卷积感受视野是局部的,需要通过叠加多层卷积区去扩大视野。另外,Max Pooling直接提取数值最大的特征,也像是hard attention的思想,直接选中某个特征。
- 在卷积操作前做Attention,比如Attention-Based BCNN-1,这个任务是文本蕴含任务需要处理两段文本,同时对两段输入的序列向量进行attention,计算出特征向量,再拼接到原始向量中,作为卷积层的输入。
- 在卷积操作后做attention,比如Attention-Based BCNN-2,对两段文本的卷积层的输出做attention,作为pooling层的输入。
- 在pooling层做attention,代替max pooling。比如Attention pooling,首先我们用LSTM学到一个比较好的句向量,作为query,然后用CNN先学习到一个特征矩阵作为key,再用query对key产生权重,进行attention,得到最后的句向量。
LSTM+Attention:LSTM内部有Gate机制,其中input gate选择哪些当前信息进行输入,forget gate选择遗忘哪些过去信息,我觉得这算是一定程度的Attention了,而且号称可以解决长期依赖问题,实际上LSTM需要一步一步去捕捉序列信息,在长文本上的表现是会随着step增加而慢慢衰减,难以保留全部的有用信息。LSTM通常需要得到一个向量,再去做任务,常用方式有:
- 直接使用最后的hidden state(可能会损失一定的前文信息,难以表达全文)
- 对所有step下的hidden state进行等权平均(对所有step一视同仁)。
- Attention机制,对所有step的hidden state进行加权,把注意力集中到整段文本中比较重要的hidden state信息。性能比前面两种要好一点,而方便可视化观察哪些step是重要的,但是要小心过拟合,而且也增加了计算量。
纯Attention:Attention is all you need,没有用到CNN/RNN,乍一听也是一股清流了,但是仔细一看,本质上还是一堆向量去计算attention。
Self-Attention优缺点
优点
参数少:self-attention的参数为$O(n^{2}d)$,而循环网络的参数为$O(nd^{2})$,卷积的参数为$O(knd^{2})$,当n远小于d时,self-attention更快
可并行化:RNN需要一步步递推才能捕捉到,而CNN则需要通过层叠来扩大感受野。Attention机制每一步计算不依赖于上一步的计算结果,因此可以和CNN一样并行处理。
捕捉全局信息:更好的解决了长时依赖问题,同时只需一步计算即可获取全局信息,在 Attention 机制引入之前,有一个问题大家一直很苦恼:长距离的信息会被弱化,就好像记忆能力弱的人,记不住过去的事情是一样的。Attention 是挑重点,就算文本比较长,也能从中间抓住重点,不丢失重要的信息。
缺点
计算量:可以看到,事实上Attention的计算量并不低。比如Self Attention中,首先要对X做三次线性映射,这计算量已经相当于卷积核大小为3的一维卷积了,不过这部分计算量还只是O(n)的;然后还包含了两次序列自身的矩阵乘法,这两次矩阵乘法的计算量都是$O(n^2)$的,要是序列足够长,这个计算量其实是很难接受的。
没法捕捉位置信息,即没法学习序列中的顺序关系。这点可以通过加入位置信息,如通过位置向量来改善,具体可以参考最近大火的BERT模型。
实践中 RNN 可以轻易解决的事,Transformer 没做到,如 复制 string,尤其是碰到比训练时的 序列更长时
Transformer vs CNN vs RNN
假设输入序列长度为$n$,每个元素的维度为$d$,输出序列长度也为$n$,每个元素的维度也是$d$。
可以从每层的计算复杂度、并行的操作数量、学习距离长度三个方面比较 Transformer、CNN、RNN 三个特征提取器。

计算复杂度
Self-Attention:考虑到 n 个 key 和 n 个 query 两两点乘,每层计算复杂度为 $O(n^2*d)$
RNN:考虑到矩阵(维度为$n*n$)和输入向量相乘,每层计算复杂度为$O(n*d^2)$
CNN:对于$k$个卷积核经过$n$次一维卷积,每层计算复杂度为$O(k*n*d^2)$。
深度可分离卷积:每层计算复杂度为 $O(k*n*d+n*d^2)$。
因此:
当$n\leq d$时,self attention 要比 RNN 和 CNN 快,这也是大多数常见满足的条件。
当$n>d$时,可以使用受限 self attention,即:计算 attention时仅考虑每个输出位置附近窗口的$r$个输入。这带来两个效果:
- 每层计算复杂度降为$O(r*n*d)$
- 最长学习距离降低为$r$,因此需要执行$O(n/r)$次才能覆盖到所有输入。
并行操作数量
可以通过必须串行的操作数量来描述
- 对于 self-attention,CNN,其串行操作数量为$O(1)$,并行度最大。
- 对于 RNN,其串行操作数量为$O(n)$,较难并行化。
最长计算路径
覆盖所有输入的操作的数量
- 对于self-attention,最长计算路径为$O(1)$;对于 self-attention stricted,最长计算路径为$O(n/r)$ 。
- 对于常规卷积,则需要$O(n/k)$个卷积才能覆盖所有的输入;对于空洞卷积,则需要$O(log_kn)$才能覆盖所有的输入。
- 对于 RNN,最长计算路径为$O(n)$
作为额外收益,self-attention 可以产生可解释性的模型:通过检查模型中的注意力分布,可以展示与句子语法和语义结构相关的信息。
参考
【论文】《Attention Is All You Need》
【github】attention-is-all-you-need-pytorch
【github】Attention_TF
【github】Attention_keras
【github】External-Attention-pytorch
【科学空间】《Attention is All You Need》浅读(简介+代码)
【华校专个人网站】Transformer的计算复杂度
【知乎问答】有了Transformer框架后是不是RNN完全可以废弃了?
【代码】Attention Is All You Need的代码
【easyaitech】一文看懂 Attention(本质原理+3大优点+5大类型)
【easyaitech】一文看懂 NLP 里的模型框架 Encoder-Decoder 和 Seq2Seq


 浙公网安备 33010602011771号
浙公网安备 33010602011771号