改变网络结构设计为什么会实现模型压缩和加速
Group convolution
Group convolution最早出现在AlexNet中，是为了解决单卡显存不够，将网络部署到多卡上进行训练而提出。Group convolution可以减少单个卷积1/g的参数量。如何计算的呢？
假设
- 输入特征的的维度为$HWC_1$;
- 卷积核的维度为$H_1W_1C_1$，共$C_2$个；
- 输出特征的维度为$H_1W_1C_2$ 。
传统卷积计算方式如下：
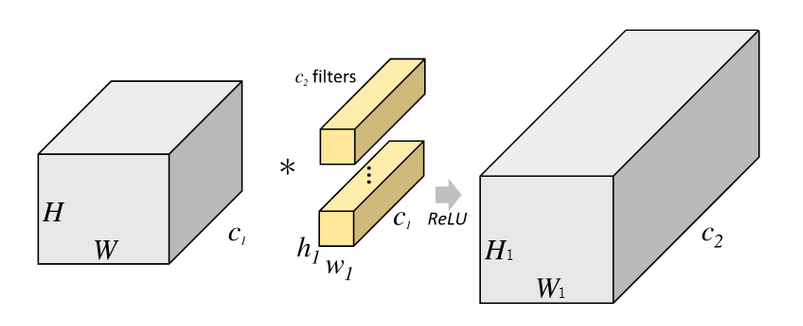
传统卷积运算量为：
$$ A = H*W * h1 * w1 * c1 * c2 $$
Group convolution是将输入特征的维度c1分成g份，每个group对应的channel数为c1/g，特征维度H * W * c1/g；，每个group对应的卷积核的维度也相应发生改变为h1 * w1 * c1/9，共c2/g个；每个group相互独立运算，最后将结果叠加在一起。
Group convolution计算方式如下：
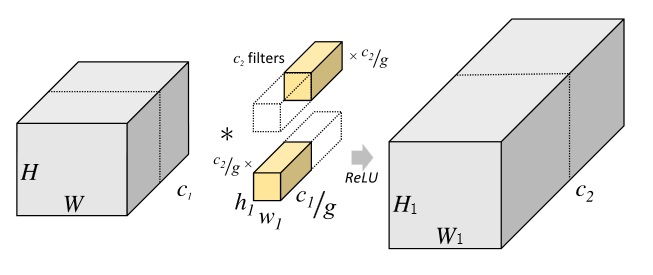
Group convolution运算量为：
$$ B = H * W * h1 * w1 * c1/g * c2/g * g $$ Group卷积相对于传统卷积的运算量：
$$ \dfrac{B}{A} = \dfrac{ H * W * h1 * w1 * c1/g * c2/g * g}{H * W * h1 * w1 * c1 * c2} = \dfrac{1}{g} $$
由此可知：group卷积相对于传统卷积减少了1/g的参数量。
Depthwise separable convolution
Depthwise separable convolution是由depthwise conv和pointwise conv构成。
depthwise conv(DW)有效减少参数数量并提升运算速度。但是由于每个feature map只被一个卷积核卷积，因此经过DW输出的feature map不能只包含输入特征图的全部信息，而且特征之间的信息不能进行交流，导致“信息流通不畅”。
pointwise conv(PW)实现通道特征信息交流，解决DW卷积导致“信息流通不畅”的问题。 假设输入特征的的维度为H * W * c1；卷积核的维度为h1 * w1 * c1，共c2个；输出特征的维度为 H1 * W1 * c2。
传统卷积计算方式如下：
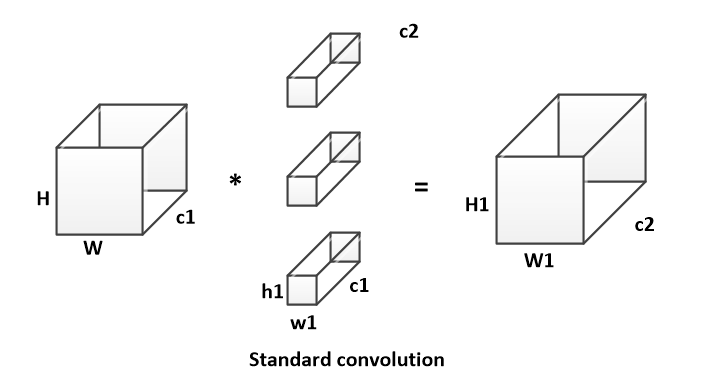
传统卷积运算量为：
$$ A = H * W * h1 * w1 * c1 * c2 $$
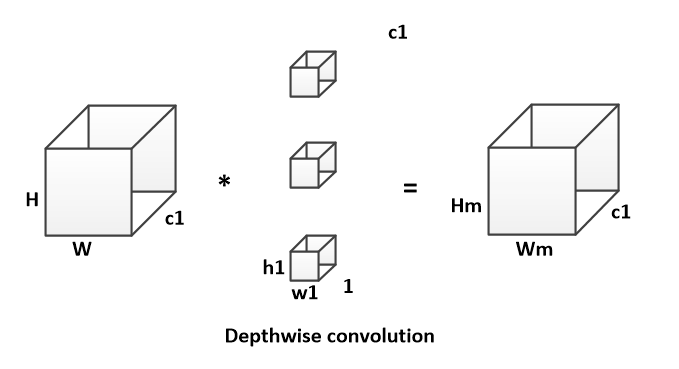
DW卷积运算量为： $$ B_DW = H * W * h1 * w1 * 1 * c1 $$
PW卷积的计算方式如下：
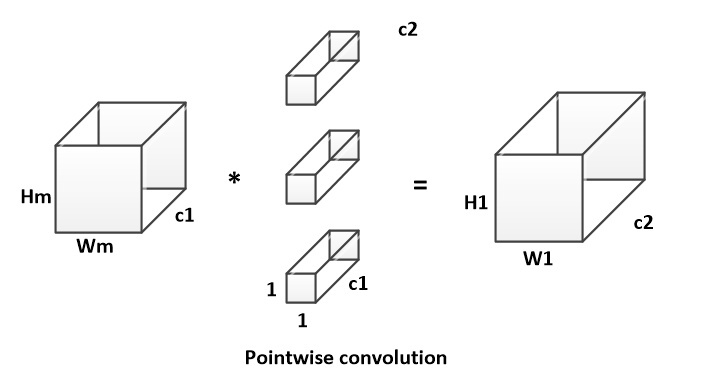
$$ B_PW = H_m * W_m * 1 * 1 * c_1 * c_2 $$
Depthwise separable convolution运算量为：
$$ B = B_DW + B_PW $$ Depthwise separable convolution相对于传统卷积的运算量：
$$ \dfrac{B}{A} = \dfrac{ H * W * h_1 * w_1 * 1 * c_1 + H_m * W_m * 1 * 1 * c_1 * c_2}{H * W * h1 * w1 * c_1 * c_2}= \dfrac{1}{c_2} + \dfrac{1}{h_1 * w_1} $$
由此可知，随着卷积通道数的增加，Depthwise separable convolution的运算量相对于传统卷积更少。
输入输出的channel相同时，MAC最小
卷积层的输入和输出特征通道数相等时MAC最小，此时模型速度最快。
假设feature map的大小为h*w，输入通道$c_1$，输出通道$c_2$。
已知：
$$ FLOPs = B = h * w * c1 * c2=> c1 * c2 = \dfrac{B}{h * w}$$
$$ MAC = h * w * (c1 + c2) + c1 * c2$$
$$ => MAC \geq 2 * h * w \sqrt{\dfrac{B}{h * w}} + \dfrac{B}{h * w} $$
根据均值不等式得到$(c1-c2)^2>=0$，等式成立的条件是c1=c2，也就是输入特征通道数和输出特征通道数相等时，在给定FLOPs前提下，MAC达到取值的下界。
减少组卷积的数量
过多的group操作会增大MAC，从而使模型速度变慢
由以上公式可知，group卷积想比与传统的卷积可以降低计算量，提高模型的效率；如果在相同的FLOPs时，group卷积为了满足FLOPs会是使用更多channels，可以提高模型的精度。但是随着channel数量的增加，也会增加MAC。
FLOPs：
$$ B = \dfrac{h * w * c1 * c2}{g} $$
MAC：
$$ MAC = h * w * (c1 + c2) + \dfrac{c1 * c2}{g} $$
由MAC，FLOPs可知：
$$ MAC = h * w * c1 + \dfrac{B*g}{c1} + \dfrac{B}{h * w} $$
当FLOPs固定(B不变)时，g越大，MAC越大。
减少网络碎片化程度(分支数量)
模型中分支数量越少，模型速度越快
此结论主要是由实验结果所得。
以下为网络分支数和各分支包含的卷积数目对神经网络速度的影响。
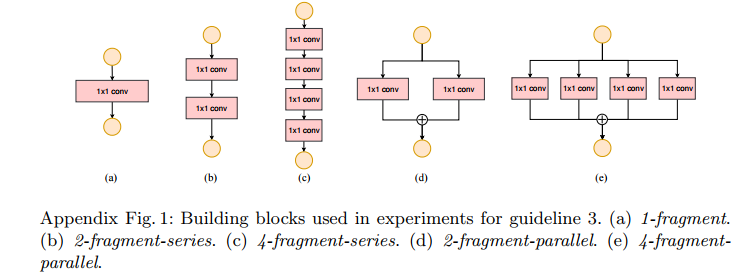
实验中使用的基本网络结构，分别将它们重复10次，然后进行实验。实验结果如下：
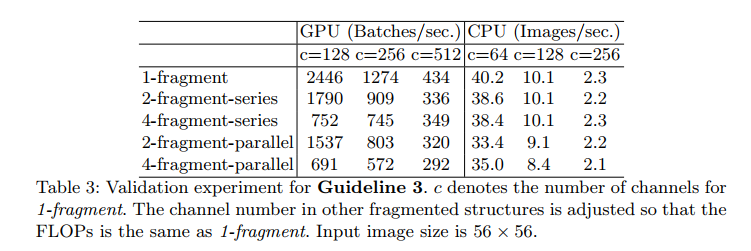
由实验结果可知，随着网络分支数量的增加，神经网络的速度在降低。网络碎片化程度对GPU的影响效果明显，对CPU不明显，但是网络速度同样在降低。
减少元素级操作
元素级操作所带来的时间消耗也不能忽视
ReLU ，Tensor 相加，Bias相加的操作，分离卷积（depthwise convolution）都定义为元素级操作。
FLOPs大多数是对于卷积计算而言的，因为元素级操作的FLOPs相对要低很多。但是过的元素级操作也会带来时间成本。ShuffleNet作者对ShuffleNet v1和MobileNet v2的几种层操作的时间消耗做了分析，发现元素级操作对于网络速度的影响也很大。
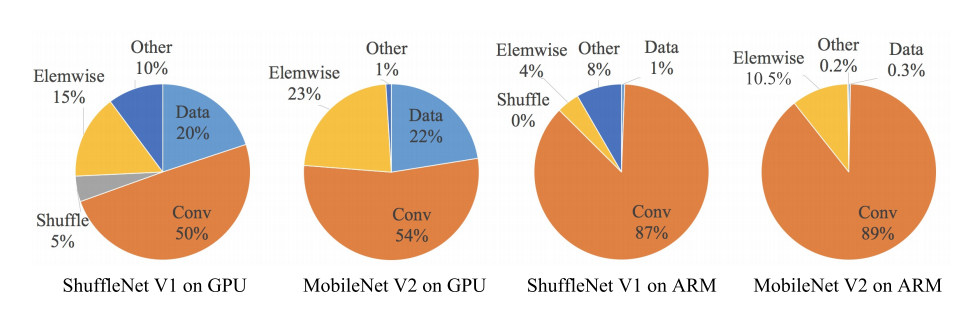
参考
【Github文章】深度学习500问
深度学习500问PDF版本
- 链接：https://pan.baidu.com/s/1jbCxM_B_D5q__446ESuaRA
- 提取码：cuup
