基于深度学习的单通道语音增强

本文代码请见：https://github.com/Ryuk17/SpeechAlgorithms

博客地址（转载请指明出处）：https://www.cnblogs.com/LXP-Never/p/14142108.html

如果你觉得写得还不错，点赞👍，关注是对我最大的支持，谢谢😃

　　传统的语音增强方法基于一些设定好的先验假设，但是这些先验假设存在一定的不合理之处。此外传统语音增强依赖于参数的设定，人工经验等。随着深度学习的发展，越来越多的人开始注意使用深度学习来解决语音增强问题。由于单通道使用场景较多，本文就以单通道语音增强为例。

　　目前基于深度神经网络单通道语音增强方法大致可以分为两类：

  • 第一种基于映射的方法
  • 第二种基于mask的方法

基于映射的语音增强

　　基于映射的语音增强方法通过训练神经网络模型直接学习带噪语音和纯净语音之间的映射关系，有两种映射方案：

频谱映射：使用模型预测语音的时频域表示，之后再将语音的时频域表示通过波形合成技术恢复成时域信号。使用最多的时频域表示特征是短时傅里叶变换谱，利用人耳对相位不敏感的特性，一般只预测短时傅里叶变换幅度谱，并使用混合语音的相位合成预测语音的波形。

波形映射：直接将带噪语音波形输入到模型，模型直接输出纯净语音波形的方法。

　　我们以频谱映射举例说明一下：

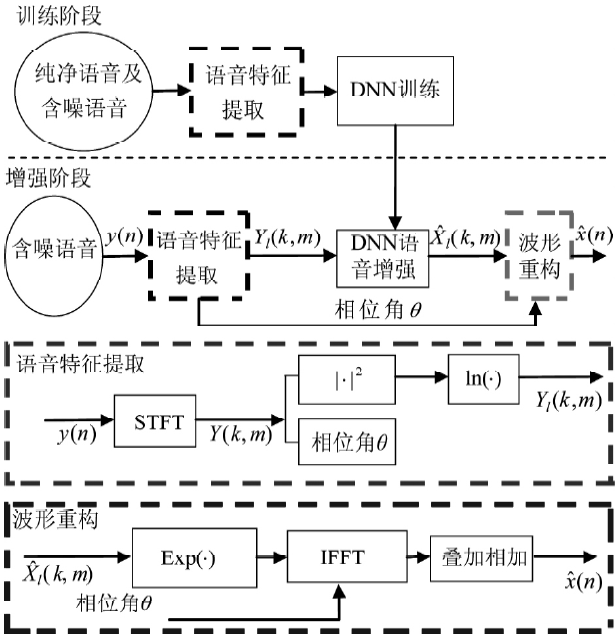
训练阶段

输入：这里采用较为简单地特征，即带噪声语音信号的幅度谱，也可以采用其他的特征。值得一提的是，如果你的输入是一帧，对应输出也是一帧的话效果一般不会很好。因此一般采用扩帧的技术，如下图所示，即每次输入除了当前帧外还需要输入当前帧的前几帧和后几帧。这是因为语音具有短时相关性，对输入几帧是为了更好的学习这种相关性

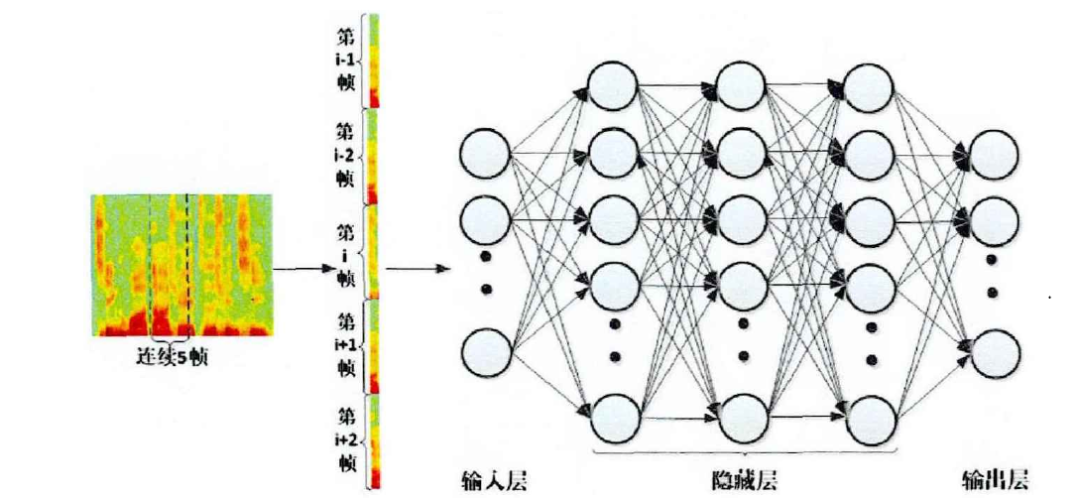
  • Label：数据的label为纯净语音信号的幅度谱，这里只需要一帧就够了。
  • 损失函数：学习噪声幅度谱与纯净语音信号的幅度谱类似于一个回归问题，因此损失函数采用回归常用的损失函数，如均方误差（MSE）、均方根误差（RMSE）或平均绝对值误差（MAE）等....
  • 最后一层的激活函数：由于是回归问题，最后一层采用线性激活函数
  • 其他：输入的幅度谱进行归一化可以加速学习过程和更好的收敛。如果不采用幅度谱可以采用功率谱，要注意的是功率谱如果采用的单位是dB，需要对数据进行预处理，因为log的定义域不能为0，简单的方法就是在取对数前给等于0的功率谱加上一个非常小的数

增强阶段

  • 输入：输入为噪声信号的幅度谱，这里同样需要扩帧。对输入数据进行处理可以在语音信号加上值为0的语音帧，或者舍弃首尾的几帧。如果训练过程对输入进行了归一化，那么这里同样需要进行归一化
  • 输出：输入为估计的纯净语音幅度谱
  • 重构波形：在计算输入信号幅度谱的时候需要保存每一帧的相位信息，然后用保存好的相位信息和模型输出的幅度谱重构语音波形，代码如下所示。
spectrum = magnitude * np.exp(1.0j * phase)

基于Mask的语音增强

Mask这个单词有的地方翻译成掩蔽有的地方翻译成掩膜，我个人倾向于翻译成“掩蔽”，本文就用掩蔽作为Mask的翻译。

时频掩蔽

　　我们都知道语音信号可以通过时域波形或者频域的各种频谱表示，此外语谱图可以同时展示时域和频域的信息，因此被广泛应用，如下图所示。语谱图上的像素点就可以称为 时频单元。

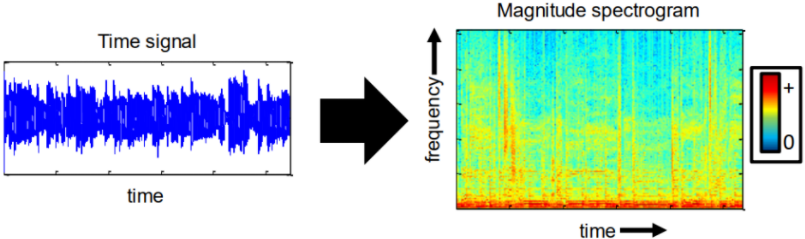
现在我们假设有两段语音信号，一段是纯净信号，另一段是噪声，他们混合在一起了，时域波形和对应的语谱图分别如下图所示：

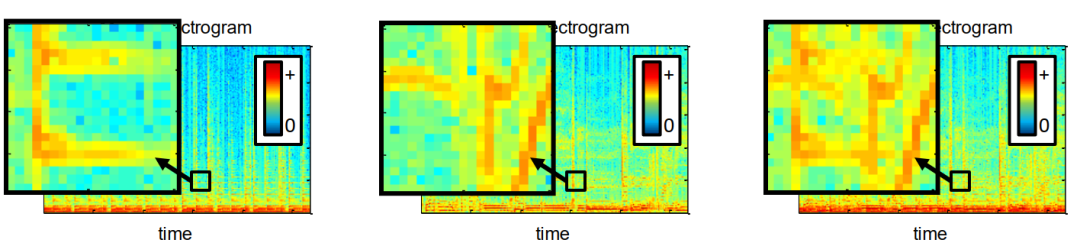
如果我们想将纯净语音信号从混合信号中抽离在时域方面是很难做到的。现在我们从语谱图（语音的时频单元）角度入手去解决语音分离问题。首先我们提出两个假设：

1、我们假设信号能量稀疏的，即对于大多数时频区域它的能量为0，如下图所示，我们可以看到大多数区域的值，即频域能量为0。

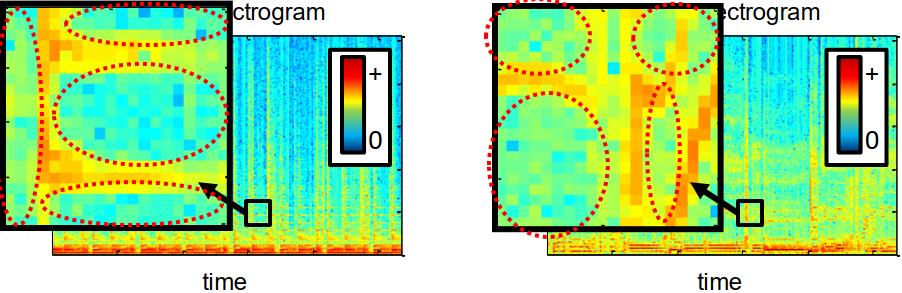
2、我们假设信号能量不相交的，即它们的时频区域不重叠或者重叠较少，如下图所示，我们可以看到时频区域不为0的地方不重叠或者有较少部分的重叠。

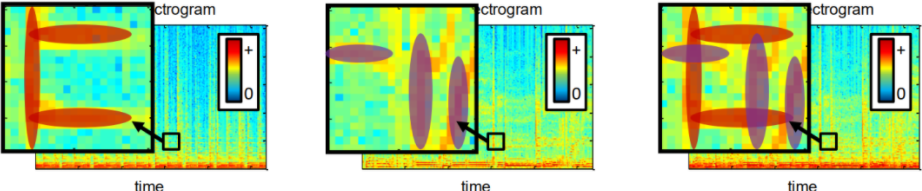
基于以上两点假设，我们就可以分离我们想要的信号和噪声信号。给可能属于一个信号源的区域分配掩码为1，其余的分配掩码0，如下图所示。

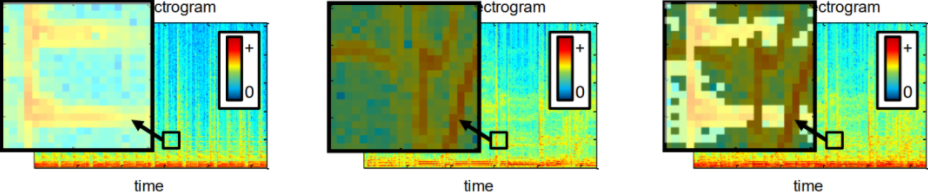
　　我们通过0和1的二值掩码然后乘以混合信号的语谱图就可以得到我们想要喜好的语谱图了，如下图所示。

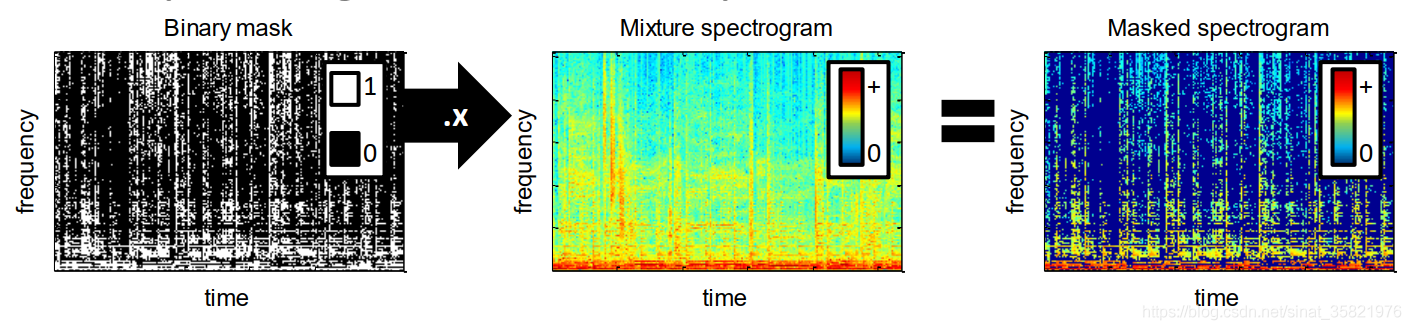
　　神经模型一般直接预测时频掩蔽$M(t,f)$，之后再通过$M(t,f)$与混合语音$Y(t,f)$相乘得到预测的纯净语音$\hat{S}(t,f)=\hat{M}(t,f)\otimes Y(t,y)$，其中$\otimes$代表哈达玛乘积(Hadamard Product)。在语音增强研究的发展过程中，研究人员提出了一系列的时频掩蔽作为训练目标：

理想二值掩蔽（Ideal Binary Mask，IBM）

原理：由于语音在时频域上是稀疏分布的，对于一个具体的时频单元，语音和噪声的能量差异通常比较大，因此大多数时频单元上的信噪比极高或极低。IBM 是对这种现实情况的简化描述，将连续的时频单元信噪比离散化为两种状态 1 和0，在一个时频单元内：如果语音占主导（高信噪比），则被标记为 1；反之如果噪声占主导（低信噪比），则标记为 0。最后将 IBM 和带噪语音相乘，实际上就是将低信噪比的时频单元置零，以此达到消除噪声的目的。

　　因此，IBM 的值由时频单元上的信噪比SNR(t,f)和设定的阈值比较之后决定：

$$公式1：I B M(t, f)=\left\{\begin{array}{l}
1,\quad if\quad |S(t,f)|^2-|N(t,f)|^2>\theta \\
0,\quad \text { otherwise}
\end{array}\right.$$

其中$\theta$为阈值，一般取0。

  • 优点：IBM 作为二值目标，只需要使用简单的二分类模型进行预测，并且可以有效地提高语音的可懂度。
  • 缺点：IBM 只有 0 和 1 两种取值，对带噪语音的处理过于粗暴，处理过程中引入了较大的噪声，无法有效地改善语音质量。

我看到过很多种写法

def IBM(clean_S, noise_S):
    """计算 ideal binary mask (IBM)
    :param clean_S: 纯净语音 STFT
    :param noise_S: 噪声 STFT
    :return: 纯净语音的理想二值掩膜 IBM
    """
    mask = np.zeros(np.shape(clean_S), dtype=np.float32)
    mask[np.abs(clean_S) >= np.abs(noise_S)] = 1.0
    return mask

第二种

def IBM_SNR(clean_speech, noise_speech):
    """计算 ideal binary mask (IBM)
    Erdogan, Hakan, et al. "Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks." ICASSP, 2015.
    :param clean_speech: 纯净语音 STFT
    :param noise_speech: 带噪语音 STFT
    :return: 纯净语音的理想二值掩膜 IBM
    """
    _eps = np.finfo(np.float).eps  # 避免除以0
    theta = 0.5  # a majority vote
    alpha = 1  # ratio of magnitudes
    mask = np.divide(np.abs(clean_speech) ** alpha, (_eps + np.abs(noise_speech) ** alpha))
    mask[np.where(mask >= theta)] = 1
    mask[np.where(mask < theta)] = 0
    return mask
第二种

第三种

def IBM_SNR(clean_speech, noise_speech,delta_size):
    """计算 ideal binary mask (IBM)
    Erdogan, Hakan, et al. "Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks." ICASSP, 2015.
    :param clean_speech: 纯净语音 STFT
    :param noise_speech: 带噪语音 STFT
    :return: 纯净语音的理想二值掩膜 IBM
    """
    _eps = np.finfo(np.float).eps  # 避免除以0
    local_snr = 0
    ibm  = np.where(10. * np.log10(np.abs(clean_speech) ** 2 / np.abs(noise_speech) ** 2) >= local_snr, 1., 0.)

    if delta_size > 0:
        ibm = ibm[:, delta_size: -delta_size]
    return ibm
View Code

理想比值掩蔽（Ideal Ratio Mask，IRM）

原理：基于语音和噪声正交，即不相关的假设下，即$S(t,f) ⋅ N(t,f) = 0$，IRM直接刻画了时频单元内纯净语音能量和带噪语音能量的比值，是目前使用非常广泛的一种掩蔽方法。

　　在这个假设下带噪语音的能量可以表示为：

$$公式2：|{Y}(t, f)|^{2}=|{S}(t, f)+{N}(t, f)|^{2}=|{S}(t, f)|^{2}+|{N}(t, f)|^{2}$$

因此得到 IRM 为：

$$公式3：I R M(t, f)=\left(\frac{|S(t, f)|^{2}}{|Y(t, f)|^{2}}\right)^{\beta} =\left(\frac{|S(t, f)|^{2}}{|S(t, f)|^{2}+|N(t, f)|^{2}}\right)^{\beta}$$

其中$\beta$为可调节尺度因子，一般取0.5。IRM取值在 0 到 1 之间，值越大代表时频单元内语音占的比重越高。另外，IRM 的平方形式就是经典的维纳滤波器（Wiener Filter），它是均方误差意义上的最优滤波器。

  • 优点：IRM 是分布在 0 到 1 的连续值，因此 IRM 是对目标语音更加准确的刻画，这使得 IRM 可以有效地同时提升语音的质量和可懂度。
  • 缺点：使用未处理的相位信息进行语音重构（相位对于感知质量也很重要）
def IRM(clean_S, noise_S, beta=0.5):
    """计算Compute ideal ratio mask (IRM)
    :param clean_S: 纯净语音 STFT
    :param noise_S: 噪音 STFT
    :return: mask
    """
    _eps = np.finfo(np.float).eps  # 防止分母出现0
    mask = np.abs(clean_S) ** 2 / (np.abs(clean_S) ** 2 + np.abs(noise_S) ** 2 + _eps)
    if beta:
        mask = mask ** 0.5
    return mask

理想幅度掩蔽（Ideal Amplitude Mask，IAM）

原理：IAM也称为Spectral Magnitude Mask（SMM），不对噪声和语音做出正交假设，IAM刻画的也是纯净语音和带噪语音的能量比值

$$公式4：\operatorname{IAM}(t, f)=\frac{|S(t, f)|}{|Y(t, f)|}$$

由于在语音和噪声叠加的过程中，存在反相相消的情况，因此并不能保证带噪语音的幅值总是大于纯净语音的幅值，因此 IAM 的范围是$[0,+\infty ]$。如果目标中出现非常大的数值，会导致训练过程出现异常。为了稳定训练，一般会将 IAM 进行截断到一定的范围内。为了确定合适的截断范围，我们可以在训练数据上采样 100 句语音并计算 IAM，就可以对IAM 的数值范围得到一个近似的估计，得到如图 3.4 的结果。一般将 IAM 截断到[0, 1]或者[0, 2]即可，因为只有非常少部分的 IAM 落在了$[2,+\infty ]$的区间内。

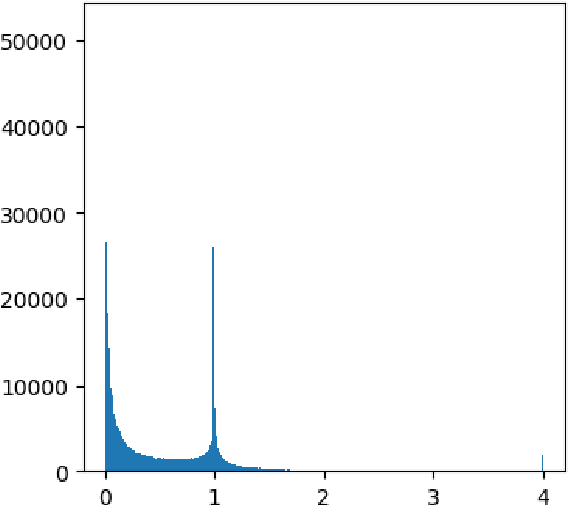
图* IAM数值分布直方图

def IAM(clean_S, noisy_S, clip=True):
    """计算ideal amplitude mask (IAM)
    :param clean_S: 纯净语音 STFT
    :param noisy_S: 带噪语音 STFT
    :return: mask
    """
    _eps = np.finfo(np.float).eps  # 避免除以0
    mask = np.abs(clean_S) / (np.abs(noisy_S) + _eps)
    if clip:
        mask = np.clip(mask, 0, 1)  # 截断到范围[0,1]

    return mask

相位敏感掩蔽（Phase Sensitive Mask，PSM）

原理：PSM考虑到相位误差的时频掩蔽

　　PSM在形式上是 IAM 乘上纯净语音和带噪语音之间的余弦相似度

$$公式5：P S M(t, f)=\frac{|S(t, f)|}{|Y(t, f)|} \cos \left(\theta^{S}-\theta^{Y}\right)$$

式中$\theta^{S}-\theta^{Y}$表示纯净语音和带噪语音的相位差，不难看出，PSM 的取值范围是$[-\infty,+\infty]$，因此也需要截断，我们同样使用直方图统计PSM的数值分布范围，从下图可以看出在0 和 1 附近出现两个明显的峰值，这也再次说明了 IBM 目标设计的合理性。为了方便，一般将 PSM 截断到[0, 1]，或者是适当将截断的区间放大到[-1, 2]。

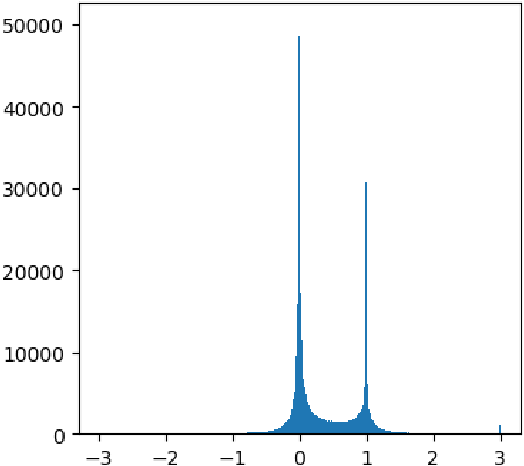 PSM数值分布直方图

  • 优点：纯净语音相位和带噪语音相位的差异，加入相位信息之后，PSM方法可以获得更高的SNR，因而降噪效果比IAM更好。
def PSM(clean_S, noisy_S):
    """计算ideal phase-sensitive mask (PSM)
    :param clean_S: 纯净语音 STFT
    :param noisy_S: 带噪语音 STFT
    :return: mask
    """
    _eps = np.finfo(np.float).eps  # 防止分母出现0

    mask = (np.abs(clean_S) / (np.abs(noisy_S) + _eps)) * np.cos(np.angle(clean_S) - np.angle(noisy_S))
    # Truncated Phase Sensitive Masking
    # Theta = np.clip(np.cos(np.angle(clean_S)-np.angle(noisy_S)), a_min=0., a_max=1.)
    # mask = np.divide(np.abs(clean_S), _eps + np.abs(noisy_S)) * Theta
    return mask

复数理想比率掩蔽（Complex Ideal Ratio Mask，cIRM）

Williamson D S, Wang Y, Wang D L. Complex ratio masking for monaural speech separation[J]. IEEE/ACM transactions on audio, speech, and language processing, 2015, 24(3): 483-492.

原理：在复数域的理想比值掩膜，同时增强幅度谱和相位谱

$$S(t,f)=M(t,f)*Y(t,f)$$

其中$S(t,f)$和$Y(t,f)$分别纯净语音和带噪语音的复数谱，$M(t,f)$是cIRM，$*$是复数乘法，其中

$$\left\{ \begin{array}{l}Y = {Y_r} + i{Y_i}\\M = {M_r} + i{M_i}\\S = {S_r} + i{S_i}\end{array} \right.==>{S_r} + i{S_i} = ({M_r} + i{M_i})*({Y_r} + i{Y_i}) = ({M_r}{Y_r} - {M_i}{Y_i}) + i({M_r}{Y_i} + {M_i}{Y_r})$$

那么：$\left\{ \begin{array}{l}{S_r} = {M_r}{Y_r} - {M_i}{Y_i}\\{S_i} = {M_r}{Y_i} + {M_i}{Y_r}\end{array} \right.$　　解方程得：$\left\{ \begin{array}{l}{M_r} = \frac{{{Y_r}{S_r} + {Y_i}{S_i}}}{{Y_r^2 + Y_i^2}}\\{M_i} = \frac{{{Y_r}{S_i} - {Y_i}{S_r}}}{{Y_r^2 + Y_i^2}}\end{array} \right.$

最终：

$$cIRM = {M_r} + i{M_i} = {\frac{{{Y_r}{S_r} + {Y_i}{S_i}}}{{Y_r^2 + Y_i^2}}} + i\frac{{{Y_r}{S_i} - {Y_i}{S_r}}}{{Y_r^2 + Y_i^2}}$$

式中，$Y$是带噪语音，$S$是纯净语音。

值得一提的是 复数掩码可能具有较大的实部分量和虚部分量，其值在$(−\infty，\infty)$的范围内。回想一下，IRM的取值范围为[0,1]，这有利于使用DNN进行监督学习。较大的取值范围可能使cIRM估计复杂化。因此，我们用下面的双曲正切压缩cIRM

$$\operatorname{cIRM}_x=K \frac{1-e^{-C \cdot M_x}}{1+e^{-C \cdot M_x}}$$

其中x是$r$或$i$，表示实分量和虚分量。这种压缩产生的掩码值在[-K, K]以内，C控制其陡度。对K和C的几个值进行了评估，K = 10和C = 0.1在经验上表现最好，并用于训练DNN。在测试期间，我们在DNN输出$O_x$上使用以下逆函数恢复未压缩掩码的估计:

$$\hat{M}_x=-\frac{1}{C} \log \left(\frac{K-O_x}{K+O_x}\right)$$

  • 优点：IRM分离语音去除了大部分噪声，但它不能像cIRM分离语音那样重建干净语音信号的实部和虚部。
def cIRM(clean_S, noisy_S, compress=True):
    """计算complex ideal ratio mask (cIRM)
    usage:
        cIRM_label = compress_cIRM(cIRM)
        loss = loss_function(cIRM_label, cIRM_pred)
        cIRM_pred = decompress_cIRM(cIRM_pred)
        enhanced_real = cIRM_pred_real * noisy_real - cIRM_pred_imag * noisy_imag
        enhanced_imag = cIRM_pred_imag * noisy_real + cIRM_pred_real * noisy_imag
    :param clean_S:纯净语音 STFT
    :param noisy_S:带噪语音 STFT
    :param compress: 获取cIRM后是否进行压缩(default=True)
    :return: cIRM
    """
    clean_real, clean_imag, = torch.real(clean_S), torch.imag(clean_S)
    noisy_real, noisy_imag, = torch.real(noisy_S), torch.imag(noisy_S)

    denominator = (noisy_real ** 2 + noisy_imag ** 2) + _eps

    cIRM_r = (noisy_real * clean_real + noisy_imag * clean_imag) / denominator
    cIRM_i = (noisy_real * clean_imag - noisy_imag * clean_real) / denominator

    # cIRM = cIRM_r + cIRM_i * 1j
    cIRM = torch.stack((cIRM_r, cIRM_i), dim=-1)
    if compress:
        cIRM = compress_cIRM(cIRM)
    return cIRM


def compress_cIRM(cIRM, K=10, C=0.1):
    """ Compress the value of cIRM from (-inf, +inf) to [-K ~ K]
    常使用双曲正切压缩cIRM
    压缩产生的掩码值在[-K,K]以内，C控制其陡度。对K和C的几个值进行了评估，K=10和C=0.1在经验上表现最好，并用于训练DNN。
    References:
        https://ieeexplore.ieee.org/document/7364200
    """
    # mask = -100,(mask<=-100)
    #        mask,(mask>-100)
    # cIRM = -100 * (cIRM <= -100) + cIRM * (cIRM > -100)   # from FullSubNet
    cIRM = K * (1 - torch.exp(-C * cIRM)) / (1 + torch.exp(-C * cIRM))
    return cIRM


def decompress_cIRM(cIRM, K=10, C=0.1):
    """ Uncompress cIRM from [-K ~ K] to [-inf, +inf]
        在测试期间，我们在DNN输出mask上使用以下逆函数恢复未压缩掩码的估计，
    References:
        https://ieeexplore.ieee.org/document/7364200

    :param cIRM: cIRM mask [cIRM_real, cIRM_imag]
    :param K: default 10
    :param C: default 0.1,FullSubNet使用 9.9
    :return:
    """
    cIRM = torch.log((K - cIRM) / (K + cIRM)) / -C
    # mask= -C,(mask<=-C)
    #        C,(mask>C)
    #        mask,(-C < mask < C)
    # mask = C * (mask >= C) - C * (mask <= -C) + mask * (torch.abs(mask) < C)
    # mask = -K * torch.log((K - mask) / (K + mask))
    return cIRM

用到cIRM的论文有：

还有一个复数比率掩膜(cRM)

最佳比例掩膜(Optimal Ratio Mask，ORM)

2013_The optimal ratio time-frequency mask for speech separation in terms of the signal-to-noise ratio

2017_Using optimal ratio mask as training target for supervised speech separation

ORM的定义是通过最小化纯净语音和估计目标语音的均方误差(MSE)来导出的

$$公式1：ORM(t, f)=\frac{|S(t, f)|^{2}+\mathcal{R}(S(t, f) N^{*}(t, f))}{|S(t, f)|^{2}+|N(t, f)|^{2}+2 \mathcal{R}(S(t, f) N^{*}(t, f))}$$

其中$S(t,f)$和$N(t,f)$分别代表纯净语音和噪声的STFT，$\mathcal{R}$代表复数的实部，$*$表示表示共轭运算。

　　可以看出，ORM与IRM非常相似，不同之处在于相干部分$\mathcal{R}\left(S(t, f) N^{*}(t, f)\right)$，在IRM中假定其为0。事实上，这个假设太过强烈了。图2显示了带噪语音中纯净语音和噪声之间的频谱一致性。我们可以看到语音和噪声是高度相关的。ORM在中被证明在语音分离方面获得了更好的性能。

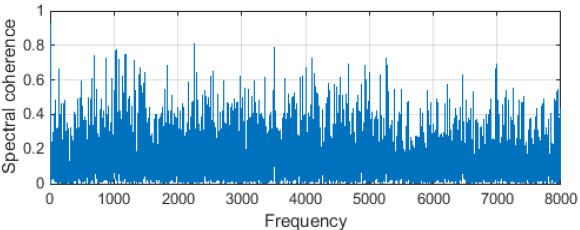
图 带噪语音中语音和噪声信号的相干估计

ORM 在$(-\infty,+\infty)$的范围内变化，这是不容易估计的。 因此，我们用双曲正切来限制 ORM 的值

$$\mathrm{ORM}(t, f)=K \frac{1-e^{-c \gamma(t, f)}}{1+e^{-c \gamma(t, f)}}$$

其中，$c=0.1$是陡度，$K=10$将 ORM 的范围限制为 (-10, +10)。$\gamma(t, f)$是公式1中定义的原始 ORM

def mask_ORM(clean_S, noise_S, K=10, C=0.1, compress=False):
    """
    :param clean_S: 纯净语音的STFT
    :param noise_S: 噪声的STFT
    :param compress:是否限制
    :return:
    """

    mag_clean = np.abs(clean_S)
    mag_noise = np.abs(noise_S)
    coherent_part = np.real(clean_S * np.conj(noise_S))  # 相干部分
    mask = (mag_clean ** 2 + coherent_part) / (mag_clean ** 2 + mag_noise ** 2 + 2 * coherent_part)
    if compress:
        mask = K * (1 - np.exp(-C * mask)) / (1 + np.exp(-C * mask))

    return mask

总结

　　语音增强中的大部分掩蔽类方法，都可以看成在特定的假设条件下cIRM 的近似。如果将 cIRM 在直角坐标系下分解，cIRM 在实数轴上的投影就是 PSM。如果再将 cIRM在极坐标系下分解，cIRM 的模值就是 IAM。而 IRM 又是 IAM 在噪声语音不相关假设下的简化形式，IBM 则可以认为是 IRM 的二值版本。

各种掩膜方法性能比较[1]：ORM > PSM > cIRM > IRM > IAM > IBM

　　上述排名并不代表所有模型和领域，像IRM、IBM等掩蔽方法，进行了某些特定的假设，所以都会在一定程度上造成性能损失。虽然 ORM 是最优掩蔽，但是使用其他简化的掩蔽方法可以降低预测的难度。这也是早期的语音增强研究选择使用 IBM 或者是 IRM 等简单掩蔽目标的原因。在模型容量有限的情况下，cIRM 经常并不是最好的选择，选择和模型建模能力匹配的目标才能获得最优的增强性能。

题外话

　　但是，这里存在一个问题，我们无法从语谱图中还原语音信号。为了解决这一问题，我们首先还原所有的频率分量，即对二值掩码做个镜像后拼接。假设我们计算语谱图时使用的是512点STFT，我们一般去前257点进行分析和处理，在这里我们将前257点的后255做镜像，然后拼接在一起得到512点频率分量，如下图所示。

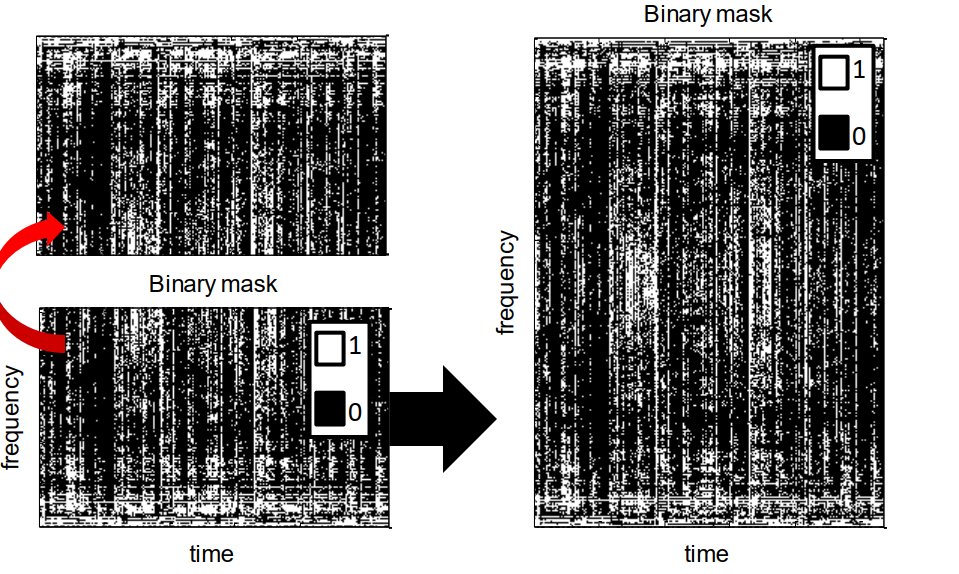
然后根据这个还原语音信号。这里指的一提的是，在进行STFT后的相位信息要保存，用于还原语音信号。

基于掩蔽的语音增强和基于映射的语音增强模型训练和增强过程类似，这里只提几个重要的地方，其余地方参考上面内容。

  • Label：数据的label为根据信噪比计算的IBM或者IRM，这里只需要一帧就够了
  • 损失函数：IBM的损失函数可以用交叉熵，IRM的损失函数还是用均方差
  • 最后一层的激活函数：IBM只有0和1两个值，IRM范围为[0,1]，因此采用sigmoid激活函数就可以了
  • 重构波形：首先用噪声幅度谱与计算的Mask值对应位置相乘，代码如下，然后根据相位信息重构语音波形。
enhance_magnitude = np.multiply(magnitude, mask)

Demo效果以及代码

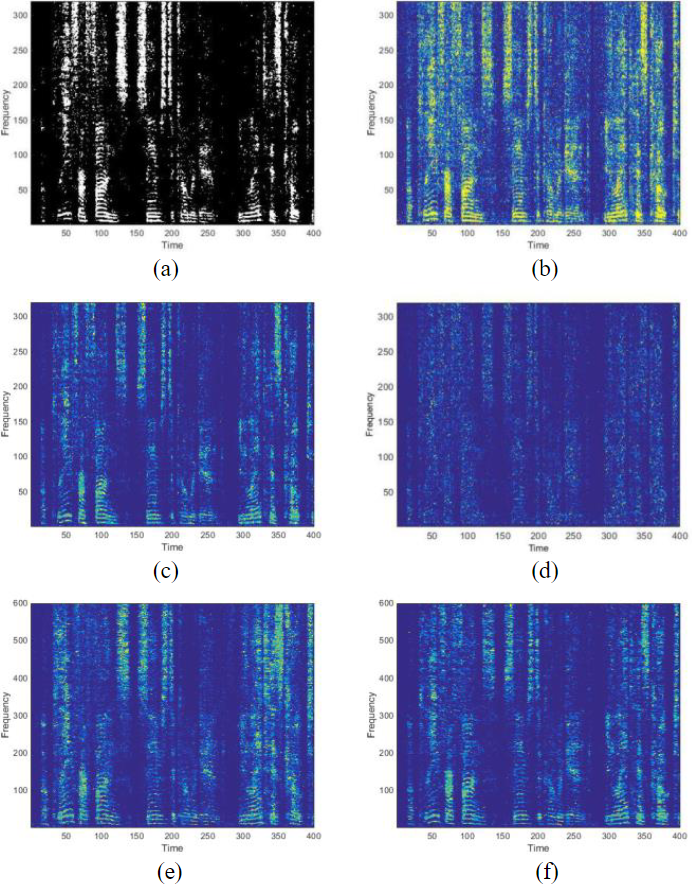
 各种蒙版目标的说明。(a)是IBM；(b)为IRM；(c)和(d)是cIRM的实部和虚部；(e)为PSM；(f) 为ORM

训练代码：

"""
@FileName: IBM.py
@Description: Implement IBM
@Author: Ryuk
@CreateDate: 2020/05/08
@LastEditTime: 2020/05/08
@LastEditors: Please set LastEditors
@Version: v0.1
"""
​
import numpy as np
import librosa
from sklearn.preprocessing import StandardScaler
from keras.layers import *
from keras.models import Sequential
​
​
def generateDataset():
    mix, sr = librosa.load("./mix.wav", sr=8000)
    clean,sr = librosa.load("./clean.wav",  sr=8000)
​
    win_length = 256
    hop_length = 128
    nfft = 512
​
    mix_spectrum = librosa.stft(mix, win_length=win_length, hop_length=hop_length, n_fft=nfft)
    clean_spectrum = librosa.stft(clean, win_length=win_length, hop_length=hop_length, n_fft=nfft)
​
    mix_mag = np.abs(mix_spectrum).T
    clean_mag = np.abs(clean_spectrum).T
​
​
    frame_num = mix_mag.shape[0] - 4
    feature = np.zeros([frame_num, 257*5])
    k = 0
    for i in range(frame_num - 4):
        frame = mix_mag[k:k+5]
        feature[i] = np.reshape(frame, 257*5)
        k += 1
​
    snr = np.divide(clean_mag, mix_mag)
    mask = np.around(snr, 0)
    mask[np.isnan(mask)] = 1
    mask[mask > 1] = 1
​
    label = mask[2:-2]
​
    ss = StandardScaler()
    feature = ss.fit_transform(feature)
    return feature, label
​
​
def getModel():
    model = Sequential()
    model.add(Dense(2048, input_dim=1285))
    model.add(BatchNormalization())
​
    model.add(LeakyReLU(alpha=0.1))
    model.add(Dropout(0.1))
​
    model.add(Dense(2048))
    model.add(BatchNormalization())
    model.add(LeakyReLU(alpha=0.1))
    model.add(Dropout(0.1))
​
    model.add(Dense(2048))
    model.add(BatchNormalization())
    model.add(LeakyReLU(alpha=0.1))
    model.add(Dropout(0.1))
​
    model.add(Dense(257))
    model.add(BatchNormalization())
    model.add(Activation('sigmoid'))
    return model
​
def train(feature, label, model):
    model.compile(optimizer='adam',
                  loss='mse',
                  metrics=['mse'])
    model.fit(feature, label, batch_size=128, epochs=20, validation_split=0.1)
    model.save("./model.h5")
​
def main():
    feature, label = generateDataset()
    model = getModel()
    train(feature, label, model)
​
​
if __name__ == "__main__":
    main()
View Code

增强代码：

"""
@FileName: Inference.py
@Description: Implement Inference
@Author: Ryuk
@CreateDate: 2020/05/08
@LastEditTime: 2020/05/08
@LastEditors: Please set LastEditors
@Version: v0.1
"""
​
import librosa
import numpy as np
from basic_functions import *
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from keras.models import load_model
​
def show(data, s):
    plt.figure(1)
    ax1 = plt.subplot(2, 1, 1)
    ax2 = plt.subplot(2, 1, 2)
    plt.sca(ax1)
    plt.plot(data)
    plt.sca(ax2)
    plt.plot(s)
    plt.show()
​
​
model = load_model("./model.h5")
data, fs = librosa.load("./test.wav", sr=8000)
​
win_length = 256
hop_length = 128
nfft = 512
​
spectrum = librosa.stft(data, win_length=win_length, hop_length=hop_length, n_fft=nfft)
magnitude = np.abs(spectrum).T
phase = np.angle(spectrum).T
​
frame_num = magnitude.shape[0] - 4
feature = np.zeros([frame_num, 257 * 5])
k = 0
for i in range(frame_num - 4):
    frame = magnitude[k:k + 5]
    feature[i] = np.reshape(frame, 257 * 5)
    k += 1
​
ss = StandardScaler()
feature = ss.fit_transform(feature)
mask = model.predict(feature)
mask[mask > 0.5] = 1
mask[mask <= 0.5] = 0
​
fig = plt.figure()
plt.imshow(mask, cmap='Greys', interpolation='none')
plt.show()
plt.close(fig)
​
magnitude = magnitude[2:-2]
en_magnitude = np.multiply(magnitude, mask)
phase = phase[2:-2]
​
en_spectrum = en_magnitude.T * np.exp(1.0j * phase.T)
frame = librosa.istft(en_spectrum, win_length=win_length, hop_length=hop_length)
​
show(data, frame)
librosa.output.write_wav("./output.wav",frame, sr=8000)
View Code

 

参考

【论文】2017_Using Optimal Ratio Mask as Training Target for Supervised Speech Separation

【论文】2016_Complex ratio masking for monaural speech separation

【论文】2015_Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks

【论文】2020_李劲东_基于深度学习的单通道语音增强研究

【博客文章】DNN单通道语音增强(附Demo代码)

【博客文章】基于Mask的语音分离

【github代码】speech-segmentation-project/masks.py

【github代码】ASP/MaskingMethods.py

【github代码】DC-TesNet/time_domain_mask.py

【github代码】ASC_baseline/compute_mask.py

【github代码】cirm.py

值得做一做的项目：

 

posted @ 2020-12-25 22:35  凌逆战  阅读(18285)  评论(25)  编辑  收藏  举报