语音信号处理——数字滤波器

模拟 / 数字滤波器

模拟滤波器（Analog Filter）是一种基于连续时间信号进行滤波的滤波器。它接受连续时间信号作为输入，并输出经过滤波处理后的连续时间信号。模拟滤波器通常使用电子元件（如电容、电感、电阻）来实现滤波功能。模拟滤波器广泛应用于模拟电路、音频放大器等领域。

计算模拟滤波器的频率响应

scipy.signal.freqs(b, a, worN=200, plot=None)

$$H(w)=\frac{b[0]*(jw)**M+b[1]*(jw)**(M-1)+...+b[M]}{ a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N]}$$

参数

b、a：线性滤波器的分子和分母，
worN：可选，如果为None，则计算响应曲线的有趣部分周围的200个频率。如果是一个整数，则计算那么多频率。

w：计算h的角频率
h：频率响应(在该频率值得振幅)

数字滤波器（Digital Filter）是一种基于数字信号进行滤波的滤波器。它接受数字信号作为输入，并输出经过滤波处理后的数字信号。数字滤波器可以通过离散化的数学算法和数字信号处理技术来实现。数字滤波器广泛应用于数字信号处理、通信系统、音频处理等领域。

计算数字滤波器的频率响应

scipy.signal.freqz(b, a=1, worN=512, whole=False, plot=None)

$$H(e^{jw})=\frac{B(e^{jw})}{A(e^{jw})}=\frac{b(1)+b(2)e^{-jw}+...+b(n+1)e^{-jwn}}{a(1)+a(2)e^{-jw}+...+a(m+1)e^{-jwm}}$$

参数

b、a：线性滤波器的分子和分母
worN：如果为None（默认值），则计算在单位圆周围等间隔的512个频率。如果是一个整数，则计算那么多频率。如果是array_like，则计算给定频率的响应（以弧度/样本为单位）。

w：计算h的频率，单位与fs相同。默认情况下，w被归一化为$[0，1)*\pi$范围(radians/sample)，例如对于一个采样频率为1000Hz的系统，300Hz则对应300/500=0.6。若要将归一化频率转换为单位圆上的弧度，则将归一化值乘以π即可。图中的0.5表示的是0.5π(rad)，即为w = 0.5π，由 w = 2 * pi * f / fs 得到 f = w * fs / 2pi，即 f = 0.5 * fs / 2 ,因为 fs = 122.88MHz，所以截止频率 f = 30.72MHz。
h：频率响应，以复数表示

数字滤波器的概念

1 数字滤波器

滤波器的作用是让有用信号尽可能无衰减地通过，对无用信号尽可能大的衰减。模拟滤波器的优点在于处理速度快、带宽大，无需ADC和DAC。但缺点是稳定性和精度较差，可重复性不好，抗干扰能力差。自20世纪60年代起，由于计算机技术、集成工艺技术和材料工业的发展，数字滤波器开始大显身手。

从广义上讲，将输入序列通过一定运算，变换成输出序列的离散时间系统（或者称为数字网络），都可以称之为数字滤波器。

从侠义上讲，数字滤波器是指输入输出均为数字信号，通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些频率成分的离散时间系统。

经典滤波器（选频滤波器、成形滤波器）是指，输入信号中有用的频率成分和希望滤除的频率成分各占有不同的频带，通过一个合适的滤波器来达到目的。

与之对应的是“现代滤波器”，例如维纳滤波器、卡尔曼滤波器、自适应滤波器等，这些滤波器可以按照随机信号内部的一些统计分布规律，从频带重叠的干扰中有效地提取信号。

本文仅涉及到经典滤波器。

滤波器的类型

滤波器系数、脉冲响应、频率响应的关系：滤波器变换，时域卷积等于频域乘积，滤波操作在时域表现为输入信号与滤波器脉冲响应的卷积；从频域上看滤波器操作表现为，输入信号的傅立叶变换和脉冲响应的傅立叶变换做乘积。

2 数字滤波器与信号处理过程

　　对于大多数应用场合，待处理信号为模拟信号，数字滤波器的前端是模数转换(ADC)，后端是数模转换(DAC)。下图为数字滤波器在整个数字信号处理过程中的位置。

也就是说，我们还要经常用到模拟角频率和数字域频率的关系。下面给出二者的公式。

$$W_0=\Omega_0T=\frac{\Omega_0}{f_s}=2\pi\frac{f_0}{f_s}$$

其中$\Omega_0$为模拟角频率(rad/s)，$f_0$为模拟频率(Hz)，$W_0$为数字域频率(rad)，$T$采样间隔(s)，$f_s$采样频率(Hz)。

3 数字滤波器的描述方法

我们学习过的离散时间系统的四种描述方法，总结如下：

差分方程：$y(n)=\sum_{i=0}^M a_i x(n-i)-\sum_{m=1}^N b_m y(n-m)$

单位冲激响应$h(n)$：$y(n)=x(n) * h(n)$

系统函数$H(z)$：$H(z)=\frac{\sum_{i=0}^M a_i z^{-i}}{1+\sum_{m=1}^N b_m z^{-m}}$

频率响应$H(e^{jw})$：$H(e^{j \omega})=\operatorname{DTFT}[h(n)]=|H(e^{jw})|e^{j\angle H(e^{jw})}=H(w)e^{j\varphi(w)}$

其中的频率响应，因为一般情况下为复函数，又分为幅频特性$|H(e^{jw})|$和相频特性$\angle H(e^{jw})$。在《数字信号处理》中，我们更偏爱于用“幅度函数$H(w)$和相位函数$\varphi(w)$”，而不是《信号与系统》中的“幅频响应和相频响应”。

数字滤波器的分类

可以从不同的角度，对数字滤波器进行不同的分类。

1 从幅频特性的角度

这是大家最熟悉的一种分类方式，根据允许通过的频带和滤除的频带不同，分为：低通滤波器(LP)、高通滤波器(HP)、带通滤波器(BP)、带阻滤波器(BS)等。

低通滤波器：只允许某一频率以下的信号无衰减地通过滤波器，其分界处的频率称为截止频率。
高通滤波器：规定高于设定临界值频率（fc）的信号能正常通过，而低于设定临界值频率(fc)的信号则被阻隔和衰减。
带通滤波器：允许特定频率信号通过的滤波器，阻隔和衰减该频带上下频率的信号。带通滤波器可以看做是由高通和低通滤波器协同作用的结果，高通和低通滤波器的截止频率可作为通带的下限频率和上限频率（图3中的L和U点）。其主要参数是中心频率和带宽，上限频率和下限频率之差就是滤波器的带宽。
带阻滤波器：能通过大多数频率分量，但将某些范围的频率分量衰减到极低水平的滤波器，与带通滤波器的概念相对。
陷波滤波器：可以在某一个频率点迅速衰减输入信号，以达到阻碍此频率信号通过的滤波效果，主要用在电路上滤除不需要的频率的信号。

当然，每一种又有模拟滤波器(AF)和数字滤波器(DF)两种形式。下图分别给出了AF及DF的四种滤波器的理想幅频响应。图中所给的滤波器的幅频特性都是理想情况，在实际上是不可能实现的。

2 从相频特性的角度

根据相位特性是否为线性的，分为：

非线性相位滤波器
线性相位滤波器

如果相位函数是w的线性函数，就称为线性相位滤波器。关于这一点，后面再说。

3 从单位冲激响应的角度

根据单位冲激响应 h(n)的长度是否有限长，分为：

有限长冲激响应（FIR）滤波器（FiniteImpulse Response Filter）
无限长冲激响应（IIR）滤波器（InfiniteImpulse Response Filter）

后面我们学习滤波器的设计、滤波器的结构，都是按照最后一种分类，将数字滤波器分为IIR和FIR，分别去学习。

以上是我们从三种不同的角度，对数字滤波器进行的分类。大家需要注意的是，不管是FIR、还是IIR，都有低通、高通、带通、带阻等。FIR，可以做到线性相位；但IIR，一般都是非线性相位的。

数字滤波器的技术指标

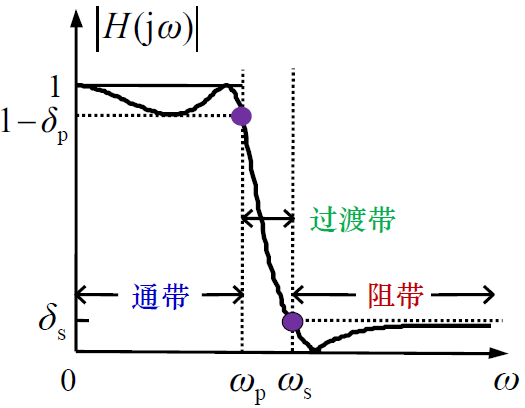
四个指标：通带截止频率$w_p$；阻带截止频率$w_s$；通带波纹$\delta_p$；阻带波纹$\delta_s$；衰减单位是db

通带内最大衰减(dB)：$R_p=-20log_{10}|H(e^{jw_p})|$

阻带内最小衰减(dB)：$A_s=-20log_{10}|H(e^{jw_{st}})|$

注意，通带截止频率，实际是指通带边沿频率，与常说的“截止频率”不同，常说的“截止频率”如不特别说明，一般指的是“3dB截止频率”。

数字滤波器的实现步骤

1、根据具体的应用背景和要求，确定技术指标

2、选择滤波器类型，(选择IIR滤波器还是FIR滤波器)

3、计算滤波器系数（通带截止频率、阻带截止频率、通带最大衰减、阻带小衰减）

4、选择滤波器的实现结构 (巴特沃斯(Butterworth)、切比雪夫(Chebyshev)和椭圆(Elliptic)滤波器)

5、用软件或者硬件来实现数字滤波器

滤波器类型：FIR / IIR 滤波器

FIR滤波器

FIR（有限冲激响应，Finite Impulse Response）滤波器 输出仅依赖于过去的输入。FIR滤波器使用非递归算法，其输出是输入信号与滤波器系数的线性组合。

特点1：系统的单位冲击响应$h(n)$有限长
特点2：只有z=0的极点，没有原点之外的极点
特点3：FIR滤波器的传递函数不包含分母，因此没有像IIR滤波器那样的反馈回路，称为非递归结构
特点4：在稳定性和相位延迟方面具有更好的特性，但可能需要更多的计算资源。

单位冲激响应：$h(n)=\left\{b_0, b_1, \ldots, b_{N-1}\right\}$

系统函数：$H(z)=\sum_{i=0}^{N-1} b_i z^{-i}$

差分方程：$y(n)=\sum_{i=0}^{N-1} b_i x(n-i)$

其中$b0, b1, ..., bn$ 是滤波器的系数，$N-1$是阶数。

　　scipy.signal.firwin 使用窗方法设计 FIR 滤波器。 scipy.signal.firwin 计算有限脉冲响应(FIR)滤波器的系数，滤波器将具有线性相位；

如果numtaps是奇数，它将是类型 I
如果numtaps是偶数，它将是类型 II，II 型滤波器在奈奎斯特频率下始终具有零响应，因此如果 firwin 以numtaps even 调用并且具有右端位于奈奎斯特频率的通带，则会引发 ValueError 异常

scipy.signal.firwin(numtaps, cutoff, width=None, window='hamming', pass_zero=True, scale=True, nyq=None, fs=None)

参数：

numtaps：滤波器的长度（系数数，即滤波器阶数 + 1）。如果通带包含奈奎斯特频率，则numtaps必须为奇数。
cutoff：滤波器的截止频率（以与fs相同的单位表示）或截止频率数组（即频带边缘）。在后一种情况下，截止频率应为正且在 0 和fs/2之间单调递增。值 0 和 fs/2不得包含在cutoff中。
width：如果width不是 None，则假设它是用于 Kaiser FIR 滤波器设计的过渡区域的近似宽度（以与fs相同的单位表示）。在这种情况下，window 参数被忽略。
pass_zero：{True, False, 'bandpass', 'lowpass', 'highpass', 'bandstop'},

True：低通，则频率 0 处的增益（即“DC gain”）为 1。
False： DC gain为 0。

返回：h：长度 numtaps FIR 滤波器的系数

IIR滤波器

IIR（无限脉冲响应，Infinite Impulse Response）滤波器 的输出依赖于过去的输入和输出。IIR滤波器使用递归算法，其输出是输入信号与过去输出信号的线性组合。

特点1：系统的单位冲激响应h(n) 无限长。
特点2：有 z 平面原点之外的极点。
特点3：流图中有反馈支路（回路），称为递归结构。
特点4：由于其递归特性，IIR滤波器可能存在稳定性和相位延迟等问题。

差分方程：$y(n)=\sum_{i=0}^M b_i x(n-i)-\sum_{i=1}^N a_i y(n-i)$

系统函数：$H(z)=\frac{B(z)}{A(z)}=\frac{b_0+b_1z^{-1}+...+b_mz^{-m}}{1+a_1 z^{-1}+...+a_nz^{-n}}=\frac{\sum_{m=0}^M b_i z^{-i}}{1+\sum_{n=1}^N a_i z^{-i}}$

$B(z)$是输入信号的加权和，$A(z)$是输出信号的加权和。$z$是复变量，表示滤波器的复域变量，$m$和$n$分子和分母多项式的阶数，一般来说，M<N，IIR滤波器的阶数是指分母多项式$z$的负幂的最大数字，例如上图中，为N阶。$B(z)$和$A(z)$决定了滤波器的频率响应特性，例如滤波器类型（低通、高通、带通等）和频率响应。

　　需要注意的是，IIR滤波器的传递函数可以有不同的表示方式，如直接形式、级联形式或者零极点形式，具体取决于滤波器的设计和实现方法。

滤波

前向滤波

scipy.signal.lfilter(b, a, x, axis=-1, zi=None)

b、a：分子和分母，即滤波器系数
x：输入数据
axis：应用线性滤波器的输入数据数组的轴。滤波器沿该轴应用于每个子阵列。默认为 -1。

y：数字滤波器的输出
zf：如果zi位None，则不返回该值，否则，zf保存最终的滤波器延迟值。

它的主要特点是：

适用于滤波器中的前向和反向滤波。
滤波是因果的，即输出信号只取决于输入信号的过去值。
可以应用各种类型的线性滤波器，包括低通、高通、带通等。

双向滤波

向前和向后对信号进行零相移（zero-phase）滤波。以消除滤波导致的相位延迟，组合滤波器的相位为零，滤波器阶数是原来的两倍。

对于大多数过滤任务，函数sosfiltfilt (以及使用 output='sos' 的滤波器设计) 应该是首选filtfilt，因为二阶部分的数值问题较少。

scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)

b、a：滤波器的分子、分母系数向量。如果a[0] 不为 1，则a和b均由a[0]归一化
x：要过滤的数据数组
axis：应用过滤器的x轴。默认为 -1。
padtype：必须是“odd”、“even”、“constant” 或 None。这决定了用于应用滤波器的填充信号的扩展类型。

返回：滤波后的数据

它的特点是：

应用了两次滤波，一次正向，一次反向，来保持信号的相位特性。
滤波器的操作通常会引入信号的延迟（相位延迟），如果信号的相位延迟会影响结果，则应该使用双向滤波保持信号相位

区别

1、相位：在正向滤波过程中，信号会受到滤波器的影响，但相位延迟会被记录下来。在反向滤波过程中，信号的相位延迟会被逆转，因此原始信号的相位变化会被反转回来。最终输出的信号将是正向和反向滤波结果的平均，这将抵消掉相位延迟的影响。

2、频响：正向滤波会引入滤波器的传递函数，而反向滤波会引入传递函数的倒数（反相）。因此，这两个传递函数的乘积可能会产生非常复杂的频率响应。在实际应用中，这可能会导致不期望的频率特性，如增益波动或失真。为了减轻这种影响，通常会使用合适的滤波器设计方法，确保滤波器的频率响应在目标范围内满足要求。此外，需要权衡保持信号相位和控制频率响应之间的关系。

import scipy.signal as signal

# 设计高通滤波器系数
fs = 16000  # 采样率
fc = 70  # 截止频率（Hz）
# 输入信号
input_signal = [0.5, 0.8, 1.0, 0.7, -0.2, -0.6, -0.8, -0.3, -0.3, -0.3, -0.3]

b, a = signal.butter(2, fc, btype='highpass', analog=False, output='ba', fs=fs)

# 使用signal.butter进行前向滤波
output_signal_butter = signal.lfilter(b, a, input_signal)
# 双向滤波
output_signal_butter2 = signal.filtfilt(b, a, input_signal)

print("Output Signal (signal.butter):", output_signal_butter)
# [ 0.49037503  0.76553894  0.93156864  0.60020224 -0.3074243  -0.6898408
#  -0.86101472 -0.33849868 -0.32602994 -0.31379498 -0.30179394]
print("Output Signal (signal.filtfilt):", output_signal_butter2)
# [ 0.5800087   0.93842344  1.19804903  0.95888962  0.12094882 -0.2157702
#  -0.35126441  0.21446924  0.28143386  0.34963254  0.41906821]

View Code

滤波器结构

　　常用的滤波器类型有：巴特沃斯（Butterworth）、切比雪夫（Chebyshev）和椭圆（Elliptic）滤波器，这些滤波器类型通常用于滤波器设计的不同要求和性能目标。它们在频率响应、陷波特性、阻带衰减等方面有所区别。

巴特沃斯滤波器

巴特沃斯滤波器是一种最常见的滤波器类型之一，其频率响应在通带中是最平滑，具有最大的通带带宽和最平滑的过渡区域。巴特沃斯滤波器的特点是不具备陷波特性，在频率响应的过渡区域中存在一定的振铃效应。

API：scipy.signal.butter

$$|H(jw)|^2=\frac{1}{1+(\frac{\omega }{\omega _c})^{2N}}$$

N：滤波器的阶数

$\omega _c$：3dB截频

典型BW低通滤波器的幅度响应

scipy.signal.butterbutter(N, Wn, btype='low', analog=False, output='ba', fs=None)

N：滤波器的阶数
Wn：截止频率，对于巴特沃斯滤波器，这是增益下降到通带$\frac{1}{\sqrt 2}$的点（即“-3db点”）。
- 对于数字滤波器：Wn与fs的单位相同Hz(fs是采样率)，在MATLAB中Wn是归一化截止频率(0,1)，Wn=截止频率/信号频率，（信号频率=采样率的一半，奈奎斯特采样定理）。归一化频率=1，截止频率$w_c$代表采样频率，0.5代表奈奎斯特频率
- 对于模拟滤波器：Wn是角频率（弧度/秒，radians/second）
btype：滤波器的类型{'lowpass'，'highpass'，'bandpass'，'bandstop'}
analog：如果为True，则返回模拟滤波器，否则返回数字滤波器。
output: {'ba'，'zpk'，'sos'}, 分子/分母（'ba'）、零点（'zpk'）或二阶部分（'sos'）。默认为“ba”表示向后兼容性，但“sos”应用于通用滤波。
fs: 采样频率

输出：

b, a: IIR滤波器的分子(' b ')和分母(' a ')多项式。仅当' ' output='ba' ' '时返回。
z, p, k: 浮点零，极点，和IIR滤波器传递函数的系统增益。仅当' ' output='zpk' ' ' '时返回。
sos：数组IIR滤波器的二阶分段表示。仅当' ' output='sos' ' '时返回。

from scipy import signal
import numpy as np
import matplotlib.pyplot as plt

fs = 16000
fc = 1000  # 截止频率

b, a = signal.butter(4, fc, btype='lowpass', analog=False, fs=fs)  # 设计N阶数字或模拟Butterworth滤波器并返回滤波器系数

w, h = signal.freqz(b, a)  # 根据系数计算滤波器的频率响应，w是角频率，h是频率响应
plt.plot(0.5 * fs * w / np.pi, np.abs(h))  # 0.5*fs*w/np.pi 为频率
plt.title('Butterworth filter frequency response')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude [dB]')
plt.grid(which='both', axis='both')  # 显示网格
plt.axvline(fc)  # 垂直线
plt.show()

提取窄带语音信号

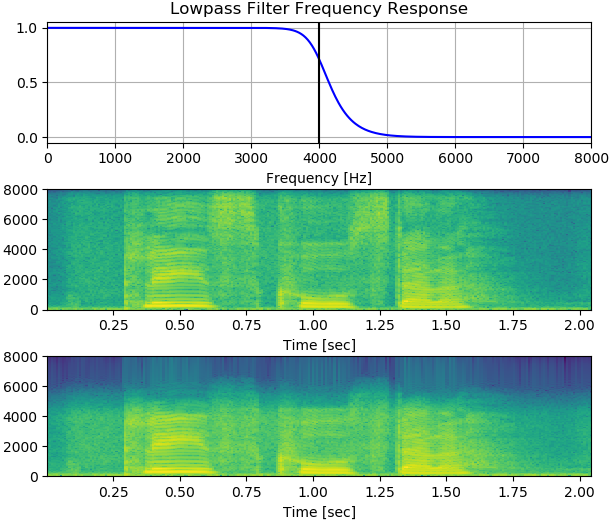
对采样率为16000Hz，奈奎斯特频率为8000Hz的语音，通过巴特沃斯低通滤波器，滤除高于4000Hz频率的语音，提取低频语音。过滤出的信号，在采样率相同的情况下，频率只有原来的一半。

import librosa 
import numpy as np
from scipy.signal import butter, lfilter, freqz
import matplotlib.pyplot as plt


def butter_lowpass(cutoff, fs, order=5):
    # cutoff：截止频率
    # fs 采样率
    nyq = 0.5 * fs                     # 信号频率
    normal_cutoff = cutoff / nyq    # 正常截止频率=截止频率/信号频率
    b, a = butter(order, normal_cutoff, btype='lowpass', analog=False)
    return b, a


def butter_lowpass_filter(data, cutoff, fs, order=5):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y  # Filter requirements.


order = 10
fs = 16000                                        # 采样率, Hz
cutoff = 4000                          # 滤波器的期望截止频率，Hz # 得到滤波器系数，这样我们就可以检查它的频率响应。
b, a = butter_lowpass(cutoff, fs, order)         # 绘制频率响应
w, h = freqz(b, a)
plt.subplot(3, 1, 1)
plt.plot(0.5*fs*w/np.pi, np.abs(h), 'b')
plt.axvline(cutoff, color='k')
plt.xlim(0, 0.5*fs)
plt.title("Lowpass Filter Frequency Response")
plt.xlabel('Frequency [Hz]')

data, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True)        # 48000--->16000
y = butter_lowpass_filter(data, cutoff, fs, order)

plt.subplot(3, 1, 2)
plt.specgram(data, Fs=16000, scale_by_freq=True, sides='default')
plt.xlabel('Time [sec]')

plt.subplot(3, 1, 3)
plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default')
plt.xlabel('Time [sec]')

plt.show()

切比雪夫滤波器

切比雪夫滤波器具有可调节的通带和阻带纹波，可以实现更陡峭的频率过渡和更高的阻带衰减。切比雪夫滤波器可以分为类型I和类型II，分别对应于不同的纹波特性。

切比雪夫I形状滤波器

CB I型低通滤波器的频域特性

$$|H(jw)|^2=\frac{1}{1+\varepsilon ^2C_N^2(\frac{w}{w_c})}$$

N：滤波器的阶数

$\varepsilon$：通带波纹

$\omega _c$：通带截频

CB I型低通滤波器的幅度响应

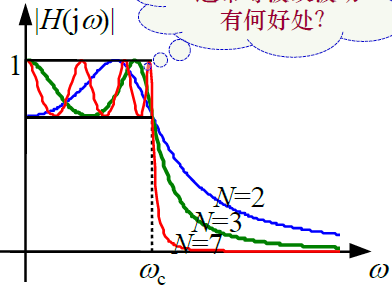
特点：通带是等波动的，阻带是单调的

scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba')

Chebyshev I型数字和模拟滤波器，设计N阶数字或模拟Chebyshev I型滤波器并返回滤波器系数。

参数：

N：滤波器的阶数
rp：通带中允许的最大纹波低于单位增益，以分贝为单位，正数
Wn：对于数字滤波器：Wn应该归一化为(0,1)，Wn=截止频率/信号频率，（信号频率=采样率的一半，奈奎斯特采样定理）对于模拟滤波器：Wn是角频率，弧度/样本，rad/s
btype：滤波器的类型{'lowpass'，'highpass'，'bandpass'，'bandstop'}
analog：如果为True，则返回模拟滤波器，否则返回数字滤波器。
output：默认“ba”,输出分子和分母

返回：b、a：滤波器系数， a为分母，b为分子。

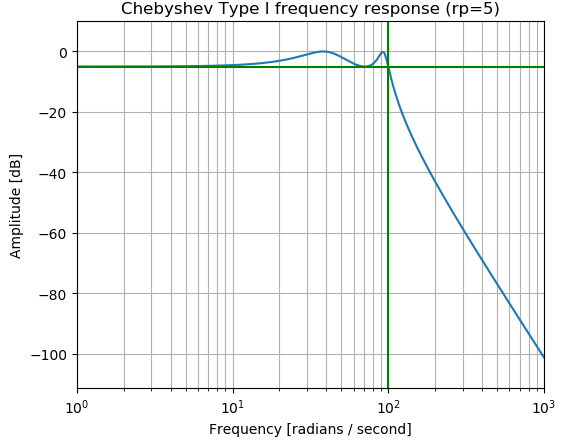
import numpy as np 
from scipy import signal
import matplotlib.pyplot as plt

b, a = signal.cheby1(4, 5, 100, 'low', analog=True)
w, h = signal.freqs(b, a)
plt.semilogx(w, 20 * np.log10(abs(h)))
plt.title('Chebyshev Type I frequency response (rp=5)')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.axhline(-5, color='green') # rp
plt.show()

切比雪夫II形状滤波器

CB II型低通滤波器的频域特性

$$|H(jw)|^2=1-\frac{1}{1+\varepsilon ^2C_N^2(\frac{w}{w_c})}$$

N：滤波器的阶数

$\varepsilon$：阻带波纹

$\omega _c$：阻带截频

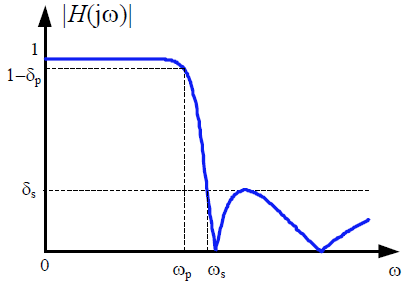
CB II型低通滤波器的幅度响应

特点：通带是单调的，阻带是等波动的

scipy.signal.cheby2(N, rs, Wn, btype='low', analog=False, output='ba')

Chebyshev II型数字和模拟滤波器，设计N阶数字或模拟Chebyshev II型滤波器并返回滤波器系数。

参数：

N：滤波器的阶数
rs：阻带所需最小衰减，以分贝为单位，正数
Wn：对于数字滤波器：Wn应该归一化为(0,1)，Wn=截止频率/信号频率，（信号频率=采样率的一半，奈奎斯特采样定理）对于模拟滤波器：Wn是角频率，弧度/样本，rad/s
btype：滤波器的类型{'lowpass'，'highpass'，'bandpass'，'bandstop'}
analog：如果为True，则返回模拟滤波器，否则返回数字滤波器。
output：默认“ba”,输出分子和分母

返回：b,a：滤波器系数， a为分母，b为分子。

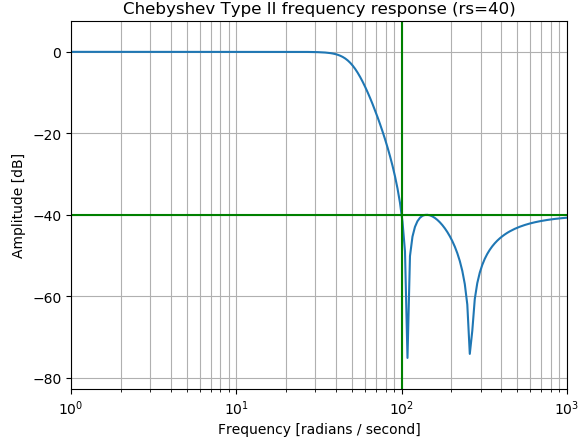
from scipy import signal
import numpy as np 
import matplotlib.pyplot as plt

b, a = signal.cheby2(4, 40, 100, 'low', analog=True)
w, h = signal.freqs(b, a)
plt.semilogx(w, 20 * np.log10(abs(h)))
plt.title('Chebyshev Type II frequency response (rs=40)')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.axhline(-40, color='green') # rs
plt.show()

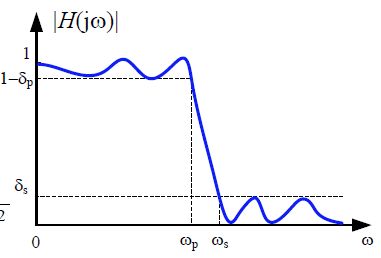
椭圆滤波器

椭圆滤波器具有最陡的过渡区域和最高的阻带衰减。椭圆滤波器在通带和阻带之间都可以实现较小的纹波，但相应的代价是频率响应不是平坦的。椭圆滤波器在阻带附近可能表现出振铃效应。

椭圆低通滤波器的幅度相应

scipy.signal.ellip(N, rp, rs, Wn, btype='low', analog=False, output='ba')

椭圆数字和模拟滤波器，设计N阶数字或模拟椭圆滤波器并返回滤波器系数。

参数：

N：滤波器的阶数
rp：通带中允许的最大纹波低于单位增益，以分贝为单位，正数
rs：阻带所需最小衰减，以分贝为单位，正数
Wn：对于数字滤波器：Wn应该归一化为(0,1)，Wn=截止频率/信号频率，（信号频率=采样率的一半，奈奎斯特采样定理）对于模拟滤波器：Wn是角频率，弧度/样本，rad/s
btype：滤波器的类型{'lowpass'，'highpass'，'bandpass'，'bandstop'}
analog：如果为True，则返回模拟滤波器，否则返回数字滤波器。
output：默认“ba”,输出分子和分母

返回：b,a：滤波器系数， a为分母，b为分子。

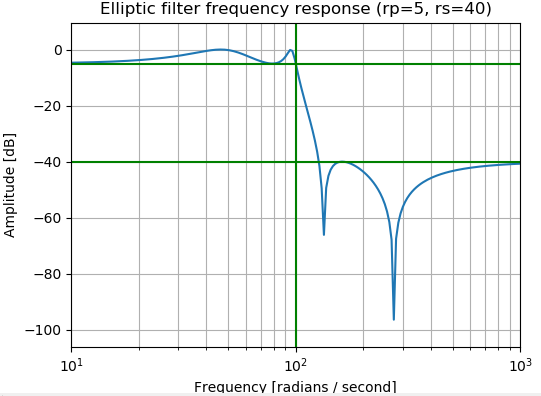
import numpy as np 
from scipy import signal
import matplotlib.pyplot as plt

b, a = signal.ellip(4, 5, 40, 100, 'low', analog=True)
w, h = signal.freqs(b, a)
plt.semilogx(w, 20 * np.log10(abs(h)))
plt.title('Elliptic filter frequency response (rp=5, rs=40)')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.axhline(-40, color='green') # rs
plt.axhline(-5, color='green') # rp
plt.show()

上采样和下采样

上采样(过采样或信号插值)，在频域上是对频谱进行了压缩，会产生周期延拓现象；

上采样流程是先通过插值模块，再通过低通滤波器，其中低通滤波器主要功能是抗周期延拓。

下采样(欠采样或信号抽取)，在频域上是对频谱进行了拓展，会产生频谱混叠现象；

下采样流程是先通过低通滤波器，再通过抽值模块，其中低通滤波器主要功能是抗频谱混叠。

注：因为降采样的时候往往无法满足采样定理，也就是很可能会发生混叠，进而失真。所以先用低通滤波器，至少得是频谱为[-1/2N,1/2N]的滤波器。

参考：在做降采样处理时，是先滤波，还是先降采样，二者有区别吗？

下采样的方法

插值方法进行下采样

Volodymyr Kuleshov的论文中使用抗混叠滤波器对语音信号进行下采样，再通过三次样条插值把下采样信号上采样到相同的长度。

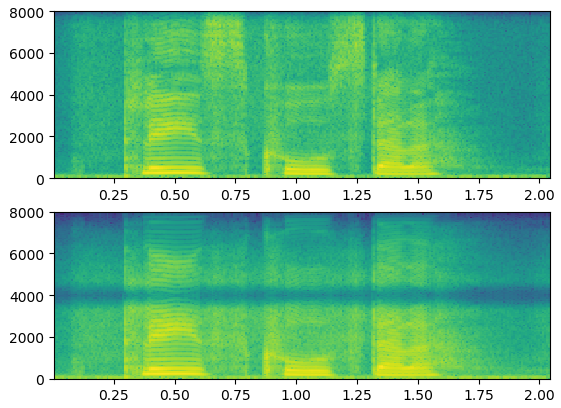
from scipy.signal import decimate
import librosa 
import numpy as np 
import matplotlib.pyplot as plt 
from scipy import interpolate

def upsample(x_lr, r):
    """
    上采样，每隔一步去掉语音波形的r个点，然后用三次样条插值的方法把去掉的点补回来，有机会可以画图看看
    :param x_lr:    音频数据
    :param r:       样条插值前个数
    :return:        样条插值后的音频信号
    """
    x_lr = x_lr.flatten()                   # 把x_lr数组折叠成一维的数组
    x_hr_len = len(x_lr) * r
    i_lr = np.arange(x_hr_len, step=r)
    i_hr = np.arange(x_hr_len)

    f = interpolate.splrep(i_lr, x_lr)      # 样条曲线插值系数
    x_sp = interpolate.splev(i_hr, f)       # 给定样条表示的节点和系数，返回在节点处的样条值

    return x_sp


yt, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True)
x_lr = decimate(yt, 2)          # 应用抗混叠滤波器后对信号进行下采样，获得低分辨率音频，下采样因子scale=2

print(len(yt))
print(len(x_lr))

plt.subplot(2, 1, 1)
plt.specgram(yt, Fs=16000, scale_by_freq=True, sides='default')

x_lr = upsample(x_lr, 2)       # 上采样
plt.subplot(2, 1, 2)
plt.specgram(x_lr, Fs=16000, scale_by_freq=True, sides='default')

plt.show()

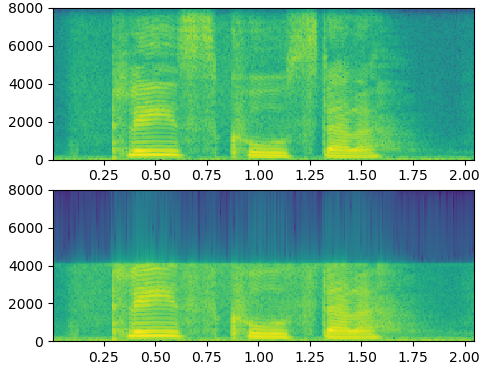
重采样(signal.resample)——下采样

利用重新采样的方法对语音进行下采样

scipy.signal.resample(x, num, t=None, axis=0, window=None)

沿给定轴使用傅立叶方法重新采样x到num个样本。因为使用傅立叶方法，所以假设信号是周期性的。

参数：

x：要重采样的数组
num：重采样信号的样本数

返回：resample_x：重新采样返回的数组

import librosa 
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt

y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) 
f = signal.resample(y, len(y)//2)
f = signal.resample(f, len(y))

plt.subplot(2,1,1)
plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default')

plt.subplot(2,1,2)
plt.specgram(f, Fs=16000, scale_by_freq=True, sides='default')

plt.show()

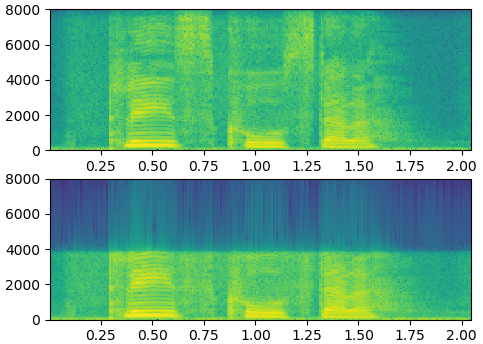
librosa.core.resample重采样(下采样)

凌振华老师的下采样方法和上面的一样

import librosa 
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt

y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) 
audio8k = librosa.core.resample(y, wav_fs, wav_fs/2)            # 下采样率 16000-->8000
audio8k = librosa.core.resample(audio8k, wav_fs/2, wav_fs)    # 上采样率 8000-->16000，并不恢复高频部分

plt.subplot(2,1,1)
plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default')

plt.subplot(2,1,2)
plt.specgram(audio8k, Fs=16000, scale_by_freq=True, sides='default')

plt.show()

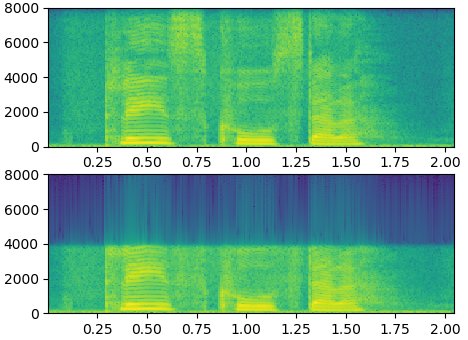
librosa.load下采样

用librosa.load想下采样，再不恢复频率的情况下上采样。

import librosa 
import matplotlib.pyplot as plt

y_16k, fs_16k = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) 
y_8k, fs_8k = librosa.load("./48k/p225_001.wav", sr=8000, mono=True) 
librosa.output.write_wav('./8k_sample.wav', y_8k, sr=8000)    # 把下采样的写好
y_8k, fs_8k = librosa.load("./8k_sample.wav", sr=16000, mono=True)     # 失去的就补不回来了


plt.subplot(2, 1, 1)
plt.specgram(y_16k, Fs=16000, scale_by_freq=True, sides='default')
plt.xlabel('16k')

plt.subplot(2, 1, 2)
plt.specgram(y_8k, Fs=16000, scale_by_freq=True, sides='default')
plt.xlabel('8k')
plt.show()