插值方法及python实现
插值interpolate模块
计算插值有两个基本方法：
1、对一个完整的数据集去拟合一个函数(一条线穿过所有数据集的点)
2、对数据集的不同部分拟合出不同的函数，而函数之间的曲线*滑对接
一维插值
interp1d(x, y, kind='linear', ...)
x和y参数是一系列已知的数据点，kind参数是插值类型，可以是字符串或整数
| 候选值 | 作用 |
| "zero"、"nearest" | 阶梯插值，相当于0阶B样条曲线 |
| ‘slinear’ 、'linear' | 线性插值，用一条直线连接所有的取样点，相当于一阶B样条曲线 |
| ‘quadratic’ 、'cubic' | 二阶和三阶B样条曲线，更高阶的曲线可以直接使用整数值指定 |
import scipy.interpolate import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import interp1d # 创建待插值的数据 x= np.array([0, 1, 2, 3, 4, 5, 6, 7]) y= np.array([3, 4, 3.5, 2, 1, 1.5, 1.25, 0.9]) xx = np.linspace(x.min(), x.max(), 1000) # 设置x的最大值和最小值以防止插值数据越界 fig, ax = plt.subplots(figsize=(8, 4)) # 返回窗口和坐标系 ax.scatter(x, y) # 绘制散点图 for n in ['linear','zero', 'slinear', 'quadratic', 'cubic', 5]: # 线性、阶梯插值、线性插值、二阶插值、三阶B样条插值 f = interp1d(x, y, kind = n) # 得到插值函数 ax.plot(xx, f(xx), label= n) ax.legend() ax.set_ylabel("y", fontsize=18) ax.set_xlabel("x", fontsize=18) plt.show()
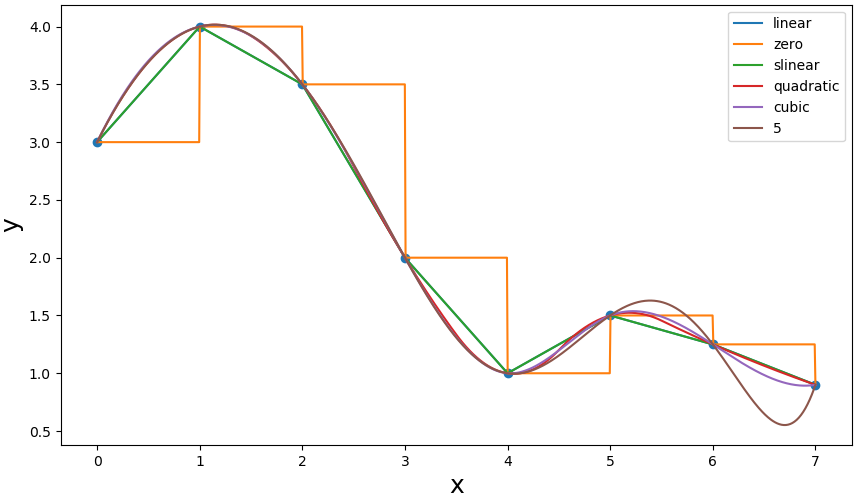
样条插值
样条插值需要两个基本步骤
1、找到一维曲线的B样条表示
scipy.interpolate.splrep(x, y, xb=None, xe=None, k=3, s=None)
参数：
- x, y：定义曲线y=f(x)的数据点
- xb, xe：float 合适的间隔，如果为None,则分别为x[0]和x[-1]
- k：样条的种类，建议使用3次样条，1 <= k <= 5
- s：float，*滑度，用户可以使用s来控制贴*度和*滑度之间的权衡。较大的s意味着更*滑，而较小的s意味着较少的*滑。
返回：
- tck：元组，(t, c, k)包含结矢量，B样条系数和样条程度的元组。
2、在期望点处评估B样条
scipy.interpolate.splev(x, tck, der=0, ext=0)
给定B样条表示的节点和系数，评估*滑多项式及其导数的值。
参数：
- x：array_like，一组点，样条的节点数
- tck：元组，由splrep返回的长度为3的系列，包含样条的阶，系数和度数。
- der：int 要计算的样条的倒数的阶数(必须小于或等于k)
返回：ndarray或ndaray列表，表示在x点处计算 的样条函数的值 的数组。
import numpy as np import matplotlib.pyplot as plt from scipy import interpolate x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8) y = np.sin(x) tck = interpolate.splrep(x, y) # 样条插值系数 xnew = np.arange(0, 2*np.pi, np.pi/50) # 插值范围 ynew = interpolate.splev(xnew, tck) plt.figure() plt.plot(x, y, 'rx') # 散点图 plt.plot(xnew, ynew, "*") # 三次样条插值 plt.plot(xnew, np.sin(xnew), "--") # True plt.plot(x, y, 'b') # 线性插图 plt.legend(["Scatter", 'Linear', 'Cubic Spline', 'True']) plt.axis([-0.05, 6.33, -1.05, 1.05]) plt.title('Cubic-spline interpolation') plt.show()
