论文翻译:Audio Bandwidth Extension
论文和代码都在这个地址。
作者:Somesh Ganesh;单位:Georgia Tech Center for Music Technology,Georgia Institute of Technology;Email:someshg94@gatech.edu
博客地址(转载请指明出处):https://www.cnblogs.com/LXP-Never/p/10129271.html
摘要
音频带宽扩展是一种利用各种音频编解码器提高有限频带音频感知质量的技术。本文提出了几种音频带宽扩展的方法,并通过听力测试对其进行了评估。比较了半波校正和全波校正,以及子带滤波的应用。结果表明,采用子带滤波的半波校正是测试算法中的最佳技术。
一、引言
在当今世界里有很多频带受限的音频,这主要是由于以下原因。信号的数字化要求对模拟信号进行采样。当模拟到数字转换器中的采样率不高时,就会产生混叠现象。为了避免这一点,反混叠滤波实现作为预处理步骤。这些滤波器基本上是低通滤波器,限制着信号的带宽。存在大量带宽被限音频的另一个原因是因为音频编解码器实现的算法,为了增加存储,音频编解码器利用这样的事实:与低频分量相比,人类对高频分量不太敏感,因此舍去了音频文件的高频分量。这样的做法可以提高存储量,并能显著提高比特率。
频带限制降低了音频的质量。因此,需要开发一种音频带宽扩展算法来恢复原始音频质量。
二、背景
让我们首先把相关工作分为两大类:盲源频带扩展和非盲源频带扩展。
A、非盲源带宽扩展
非盲带宽扩展是指利用特定的编码和解码技术重建缺失频谱的过程。这包括一些时域或频率信息、噪声水平或在对信号进行编码时缺失的频率分量以及低频分量有关的任何其他相关信息。最著名的非盲源带宽扩展算法之一是频谱折叠(SBR)[1]。该方法有自己的编解码器,其工作原理是假设低频分量与高频分量有很强的相关性。利用逆滤波、自适应加噪和正弦再生等技术,对相关系数较低的信号进行了分析。[2]提出了一种利用分形自相似模型(FSSM)对音频信号进行修正离散余弦变换(MDCT)表示的算法。该方法用于多种音频信号,并对缺失频谱进行了细节的重建。[3]引入精确谱替换(ASR)技术,对缺失频谱中的色调分量和谐波结构进行重建。[4]使用[2]和[3]中的概念,并将它们应用于信号的高频分辨率表示,如MDCT。它还包括“多波段时域幅度编码”(Mbtac),用于重构高频分量的时间整形。这些方法的问题在于,该过程需要额外的信道资源来传输有关缺失频谱的信息。当对比特率和存储有限制时,这是不可取的。
B、盲源带宽扩展
盲源带宽扩展是指在没有任何缺失频谱的前提情况下进行重建的过程。[5]提出了一种基于半波整流的盲源带宽扩展算法。该方法对频带被限信号中的最高倍频程采用半波整流法,产生高频谱。这个新的频谱通过增益因子进行缩放,并被添加到延迟输入信号中。[6]通过提出一种不同的过滤最高倍频程的方法来优化这一过程以实现实时应用。该方法还包括作为预处理步骤的带宽检测模块和作为后处理步骤的自适应增益。[7]和[8]建议采用线性外推法求出高频谱的包络并进行重构。文[9]中的算法是基于相位空间重构(PSR)的方法。这里,PSR被用来将宽带音频的低频MDCT系数转换成多维空间。高频频谱根据听者的感知进行调整。这包括线性和非线性预测。[10]提出了基于混沌预测理论的算法,并建议根据音频产生原理和人耳知觉生成高频信息。
三、算法
本论文所使用的算法是一种盲带宽扩展算法。这是因为目前频带受限的音频数据集很大并且没有原始音频。在这种情况下,非盲源频带扩展不会有多大作用。首先让我们简要地看一下图一中实现的系统框图。

图1:算法概述
A、滤波器1
这一部分对频带受限音频进行的滤波操作。在此过程中,提取信号的最高倍频程。假设信号中的最高频率分量是$f_{hf}$。现在,假设信号中的采样频率$fs≥4*f_{hf}$,这可以在预处理步骤中对信号进行采样。信号中的最高倍频程在$\frac{f_{hf}}{2}-f_{hf}$之间。在下一个模块非线性设备(NLD)中用滤波后的信号来生成缺失的高频谱。非线性设备(NLD)产生互调失真(在下一节中定义)。为了研究这种失真对系统质量的影响,该模块我们设计了两个不同的版本。第一版本是一个简单的IIR(无限脉冲响应)带通滤波器,它允许$\frac{f_{hf}}{2}-f_{hf}$范围的频率通过。互调失真随频率分量的增加而增加。第二个版本是两个IIR带通滤波器的组合,其中第一个滤除信号中最高倍频程的一半,而另一个滤除另一半。
B、非线性设备 Non-Linear Device(NLD)
该部分由非线性设备组成,该部分利用来自上一模块中滤波后的信号产生高频谱。这部分产生信号的高频谐波。在这里,我们使用了两个非线性设备。一个是半波整流器,另一个是全波整流器。我们选择了整改,因为这是一个均匀的过程。整流器的输出主要是输入频率的二次谐波,二次谐波的衰减为12dB每倍频程。半波整流输出的频谱由原始输入频率和所有谐波组成。另一方面,全波整流输出的频谱仅由输入频率的谐波组成。我们对产生的谐波感兴趣,即$f_{hf}-2*f_{hf}$之间的频谱。接下来,让我们来定义互调失真(IMD)。当一个频率分量由两个或两个以上的频率分量组成,经过非线性设备运算时,输出不仅包含这些频率分量,而且还包含几个不理想的分量,这些分量基本上是输入分量的总和差。输出中的这种失真称为互调失真。本文研究了半波互调失真和全波整流对重建音频信号主观质量的影响。
C、滤波器2
这一部分在非线性设备(NLD)模块后面,我们之前的NLD模块仅关注高频谱的生成,经过上一模块的整流之后,高频分量将主要包含输入频率分量的二次谐波。由于互调失真,会出现低于$f_{hf}$和高于$2*f_{hf}$的不良成分。这些分量需要消除。因此,目标信号将位于$f_{hf}$和$2*f_{hf}$之间。在这个阶段,这些边界之间的信号将被过滤掉。类似于滤波器1模块,这个模块我们有来两个版本。第一个版本将包含一个简单的IIR带通滤波器,它将滤除$f_{hf}$和$2*f_{hf}$之间的信号。第二个版本包含两个独立的IIR带通滤波器。当使用第二版本的滤波器1时,再使用这个版本的滤波器2。第一个滤波器将会滤除第二版本滤波器1的输入频率的二次谐波。第二滤波器将会滤除滤波器1中第二版本的第二滤波器输入频率产生的二次谐波。这样可以增加这两个滤波器的输出,使我们得到完整的重构高频谱。
最后,将产生的高频频谱添加到输入中,输入延迟的量相当于产生频谱所需的时间。因此,我们最终有频带扩展的信号。
四、评估
A、试验方法与技术
在评估方面,进行听力测试来证明带宽扩展音频的主观质量。实验数据集是用一个简单的IIR低通滤波器生成的。五首歌来自不同的流派-电子,摇滚,电子屋,声学和世界音乐。所有音频文件的采样频率都为44.1kHz,带宽限制为7 kHz。每个文件都有20秒长。
对于听力测试,进行了MUSHRA[11]样试验。首先让参与者听到原始的音频文件(参考),然后是带宽受限的音频文件。之后,他们按随机顺序听到五个音频文件,其中包括一个隐藏的参考音频。另外四个音频文件是使用上述算法经过频带扩展的音频文件。
- 半波整流;
- 基于子带滤波的半波整流
- 全波整流;
- 基于子带滤波的全波整流
然后对这些音频文件的评分按1到10划分等级,1是感知质量的最差的等级,10是感知质量的最好的等级。重复播放这5首歌,所有音频文件的响度均方值标准化为0.7。
其中一首歌曲的所有5个音频文件的频谱图图以及频带受限信号如下图2所示。

图2a,原始语音信号(参考信号)
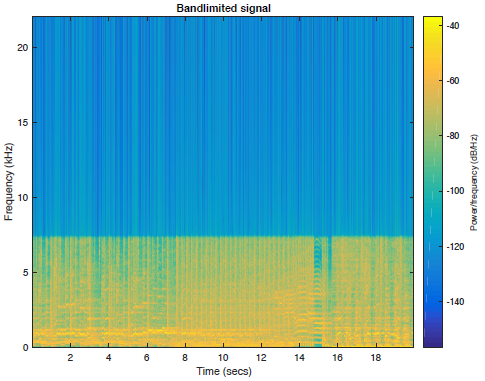
图2b:频带受限语音信号
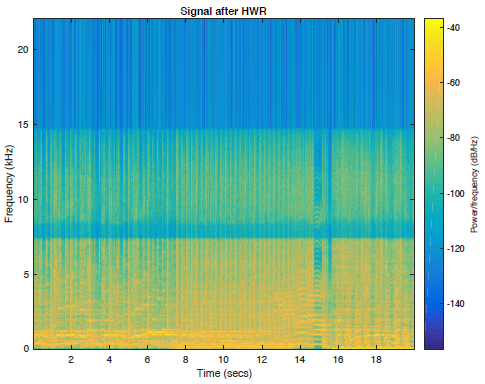
图2c:半波整流重建后的信号
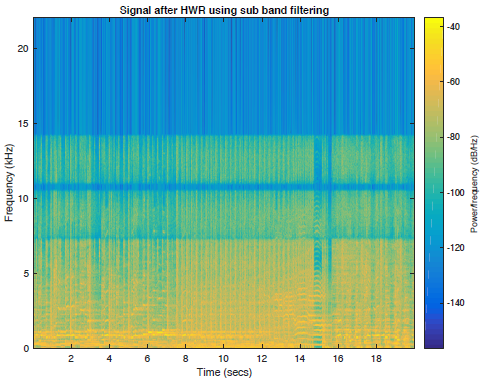
图2d:半波整流和子带滤波重建信号
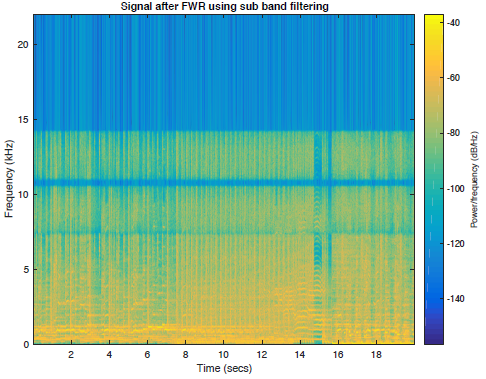
图2e:全波整流重建信号
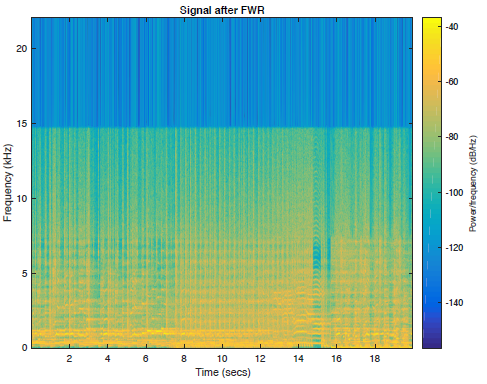
图2f:全波整流和子带滤波重建信号
B、结果
测试有6名参与者。记录结果,计算评分均值。这些数字列于表1。
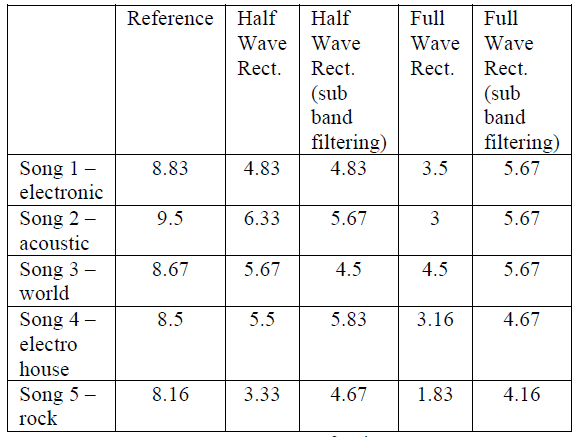
表1:评估方法
从结果可以看出,原始音频文件(参考)获得最高的评分。这就告诉我们,参与者给出的评分是真实的,是可以考虑的。
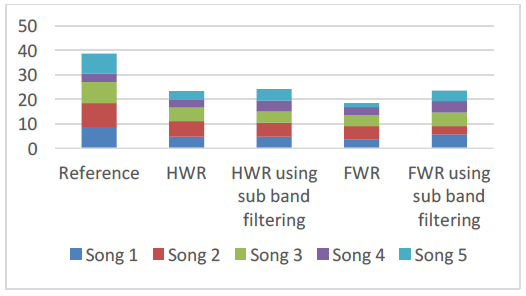
图3:评估方法的柱形图
从图3中的条形图中,我们可以看到原始音频文件比带宽扩展后的音频文件具有更好的质量。我们还可以看到,在算法中使用子带滤波对音频文件的主观质量有积极的影响。使用简单的全波整流做音频扩展得到的音频文件中发现,在所有音频文件中,感知质量的得分最少。
五、论述
首先,对本文提出的算法和实验结果进行了讨论。
结果表明,采用子带滤波可以降低重建输出的互调失真,因此具有较高的主观的得分。我们还可以得出结论,与全波整流相比,半波整流是一种更好的方法。根据所收到的评分,我们可以根据感知质量的得分对算法进行排序。
- 基于子带滤波的半波整流
- 基于子带滤波的全波整流
- 半波整流;
- 全波整流;
这些结果验证了文献[6]所提出的方法,即子带滤波的使用预期具有较高的感知质量,但是未与文献[5]中使用的一般滤波技术相比较。本文还比较了半波整流与全波整流对感知质量的影响。
接下来,让我们来讨论一下本文提出的算法和实验的缺点:
1、该算法只有当频带限制音频信号$f_{hf}=\frac{f_s}{4}$中存在最高频率的情况下,才能将频谱重构到最大极限$\frac{fs}{2}$。如果$f_{hf}<\frac{f_s}{4}$,如图2所示,我们无法在最大范围内重建高频频谱。
2、所进行的实验只有很少的参与者和一个很小的数据集。
六、展望工作
本文可作为今后音频带宽扩展工作的基本框架。以下是本文算法和实验的改进和扩展。
- 高频谱的重建可以独立于频带受限音频中的最高频率。这将允许适当的重建,即使信号中的最高频率很低,即在5-7kHz的范围内。
- 在本文中由于在非线性设备模块中只使用了两种不同的整流器,因此可以对不同的非线性设备(如积分器)进行进一步的研究。
- 整个系统可以进一步优化,以更好地实时工作。
七、结论
本文对不同的音频带宽扩展方法进行了比较,并通过听力测试对结果进行了评价。实验结果表明,半波整流作为一种非线性设备,其校正效果优于全波整流,采用子带滤波可以提高带宽扩展信号的感知质量。
八、参考文献
[1] P. Ekstrand, “Bandwidth extension of audio signals by spectral band replication,” in Proceedings of the 1st IEEE Benelux Workshop on Model Based Processing and Coding of Audio (MPCA ’02, 2002.)
[2] Deepen Sinha, Anibal Ferreira, and, Deep Sen “A Fractal Self-Similarity Model for the Spectral Representation of Audio Signals,” 118th Convention of the Audio Engineering Society, May 2005, Paper 6467.
[3] Anibal J. S. Ferreira and Deepen Sinha, “Accurate Spectral Replacement,” 118th Convention of the Audio Engineering Society, May 2005, Paper 6383.
[4] H. E. V., A. J. S. Ferreira, and D. Sinha, “A Novel Integrated Audio Bandwidth Extension Toolkit (ABET),” presented at the Audio Engineering Society Convention 120, 2006.
[5] E. Larsen, R. M. Aarts, and M. Danessis, “Efficient High-frequency Bandwidth Extension of Music and Speech,” presented at the Audio Engineering Society Convention 112, 2002.
[6] M. Arora, J. Lee, and S. Park, “High Quality Blind Bandwidth Extension of Audio for Portable Player Applications,” presented at the Audio Engineering Society Convention 120, 2006.
[7] C.-M. Liu, W.-C. Lee, and H.-W. Hsu, “High Frequency Reconstruction for Band-Limited Audio Signals,” in Proceedings of the 6th International Conference on Digital Audio Effects (DAFX-03), 2003.
[8] “AES E-Library » High Frequency Reconstruction by Linear Extrapolation.” [Online]. Available: http://www.aes.org/elib/browse.cfm?elib=12426.
[9] C.-C. Bao, X. Liu, Y.-T. Sha, and X.-T. Zhang, “A blind bandwidth extension method for audio signals based on phase space reconstruction,” EURASIP Journal on Audio, Speech, and Music Processing, vol. 2014, no. 1, p. 1, 2014.
[10] Y. T Sha, C. C Bao, M. S Jia, and X. Liu, “High frequency reconstruction of audio signal based on chaotic prediction theory,” in 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, 2010, pp. 381–384.
[11] The MUSHRA audio subjective test method - BBC R&D, 2002.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号