TensorFlow 基础概念解析
• TensorFlow模块与架构介绍
以下资料来源于极客时间学习资料
TensorFlow 模块与 APIs


• TensorFlow数据流图介绍
TensorFlow数据流图是一种声明式编程范式
声明式编程与命令式编程的多角度对比

斐波拉契数列示例

TensorFlow数据流图
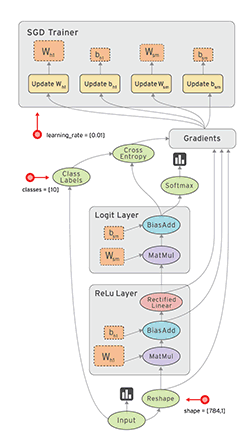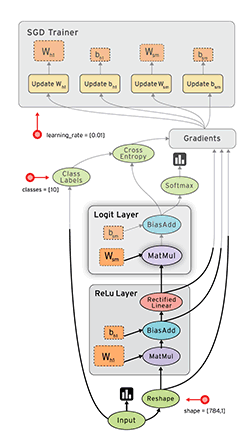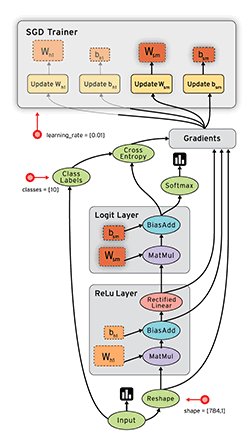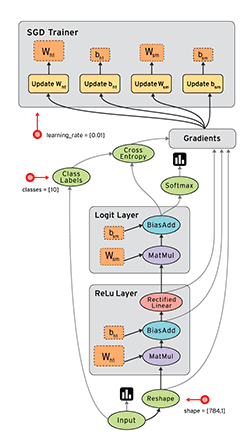

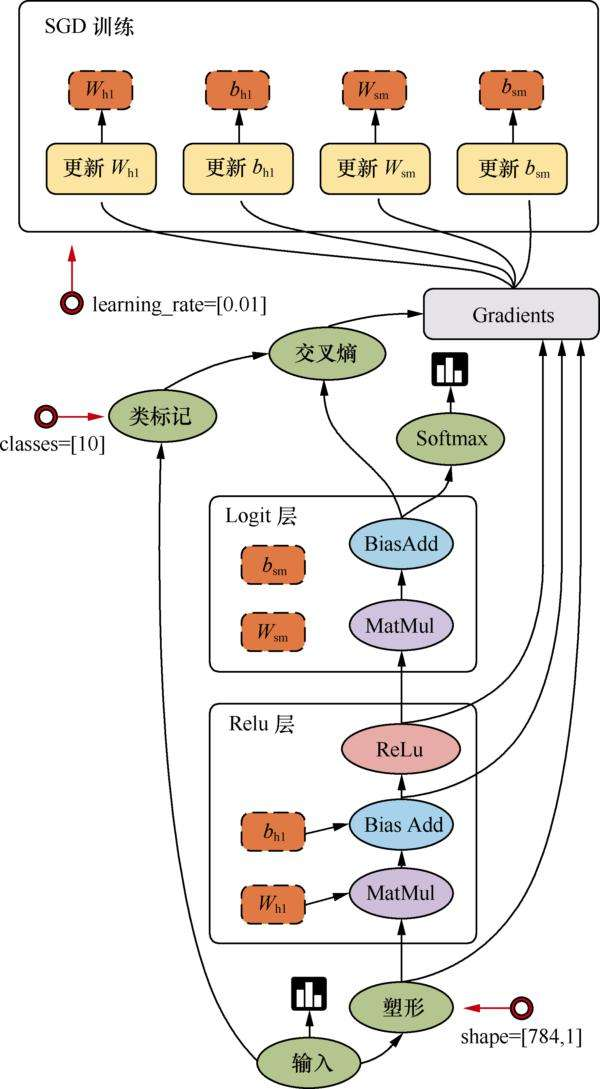

TensorFlow数据流图优势
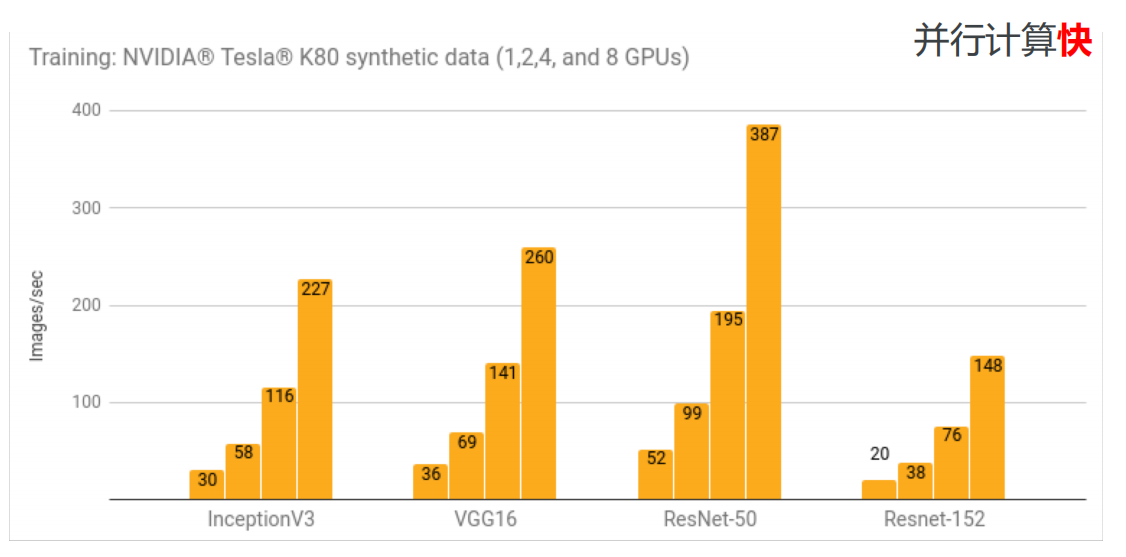
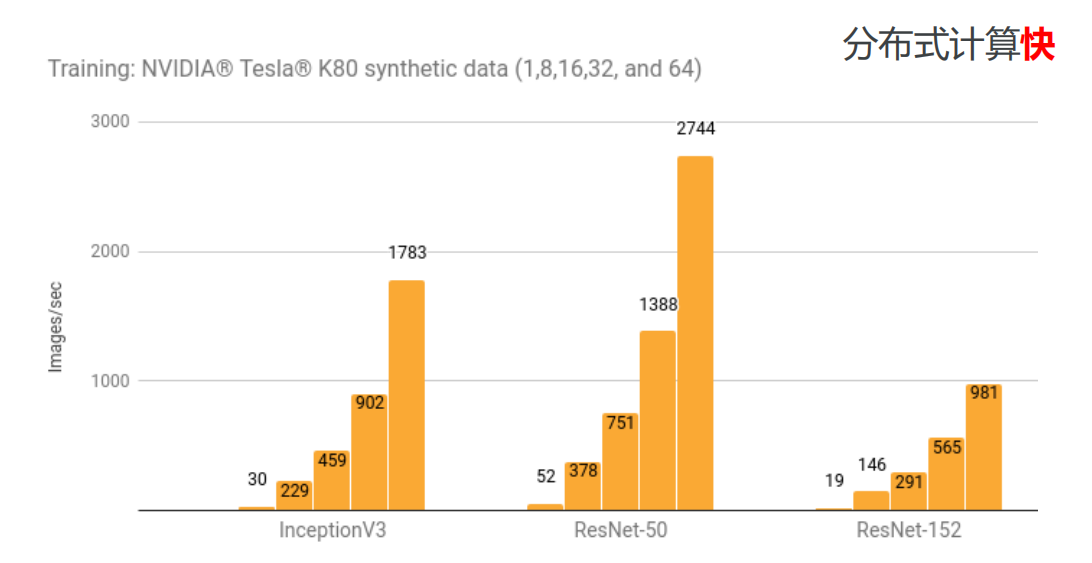
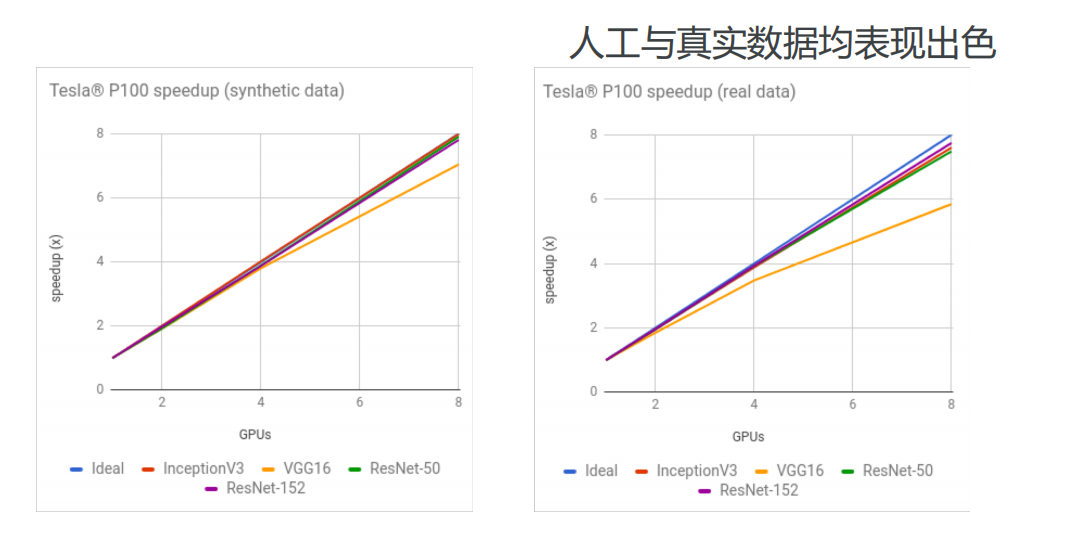
• 并行计算快
• 分布式计算快(CPUs, GPUs TPUs)
• 预编译优化(XLA)
• 可移植性好(Language-independent representation)
• 张量(Tensor )是什么 • 变量(Variable )是什么
在数学里,张量是一种几何实体,广义上表示任意形式的“数据”。张量可以理解为 0 阶(rank ) 标量、
1 阶向量和 2 阶矩阵在高维空间上的推广,张量的阶描述它表示数据的最大维度。

在TensorFlow中,张量(Tensor )表示某种相同数据类型的多维数组。
因此,张量有两个重要属性:
1. 数据类型(如浮点型、整型、字符串)
2. 数组形状(各个维度的大小)

Q : TensorFlow张量是什么?
• 张量是用来表示多维数据的
• 张量是执行操作时的输入或输出数据。
• 用户通过执行操作来创建或计算张量。
• 张量的形状不一定在编译时确定,可以在运行时通过形状推断计算得出。
在TensorFlow中,有几类比较特别的张量,由以下操作产生:
• tf. constant //常量
• tf. placeholder //占位符
• tf. Variable //变量
测试代码:
import tensorflow as tf # 0阶张量 mammal = tf.Variable("Elephant", tf.string) ignition = tf.Variable(451, tf.int16) floating = tf.Variable(3.14159265359, tf.float64) its_complicated = tf.Variable(12.3 - 4.85j, tf.complex64) [mammal, ignition, floating, its_complicated] Out[3]: [<tf.Variable 'Variable:0' shape=() dtype=string_ref>, <tf.Variable 'Variable_1:0' shape=() dtype=int32_ref>, <tf.Variable 'Variable_2:0' shape=() dtype=float32_ref>, <tf.Variable 'Variable_3:0' shape=() dtype=complex128_ref>] # 1阶张量 mystr = tf.Variable(["Hello", "World"], tf.string) cool_numbers = tf.Variable([3.14159, 2.71828], tf.float32) first_primes = tf.Variable([2, 3, 5, 7, 11], tf.int32) its_very_complicated = tf.Variable([12.3 - 4.85j, 7.5 - 6.23j], tf.complex64) [mystr, cool_numbers, first_primes, its_very_complicated] Out[6]: [<tf.Variable 'Variable_8:0' shape=(2,) dtype=string_ref>, <tf.Variable 'Variable_9:0' shape=(2,) dtype=float32_ref>, <tf.Variable 'Variable_10:0' shape=(5,) dtype=int32_ref>, <tf.Variable 'Variable_11:0' shape=(2,) dtype=complex128_ref>] # 2阶张量 mymat = tf.Variable([[7],[11]], tf.int16) myxor = tf.Variable([[False, True],[True, False]], tf.bool) linear_squares = tf.Variable([[4], [9], [16], [25]], tf.int32) squarish_squares = tf.Variable([ [4, 9], [16, 25] ], tf.int32) rank_of_squares = tf.rank(squarish_squares) mymatC = tf.Variable([[7],[11]], tf.int32) [mymat, myxor, linear_squares, squarish_squares, rank_of_squares, mymatC] Out[5]: [<tf.Variable 'Variable_8:0' shape=(2, 1) dtype=int32_ref>, <tf.Variable 'Variable_9:0' shape=(2, 2) dtype=bool_ref>, <tf.Variable 'Variable_10:0' shape=(4, 1) dtype=int32_ref>, <tf.Variable 'Variable_11:0' shape=(2, 2) dtype=int32_ref>, <tf.Tensor 'Rank:0' shape=() dtype=int32>, <tf.Variable 'Variable_12:0' shape=(2, 1) dtype=int32_ref>] # 4阶张量 my_image = tf.zeros([10, 299, 299, 3]) # batch x height x width x color my_image Out[7]: <tf.Tensor 'zeros:0' shape=(10, 299, 299, 3) dtype=float32>
变量(Variable )是什么
TensorFlow变量(Variable)的主要作用是维护特定节点的状态, 如深度学习或机器学习的模型参数。
tf.Variable 方法是操作,返回值是变量(特殊张量)。
通过tf.Variable方法创建的变量,与张量一样,可以作为操作的输 入和输出。不同之处在于:
- 张量的生命周期通常随依赖的计算完成而结束,内存也随即释放。
- 变量则常驻内存,在每一步训练时不断更新其值,以实现模型参 数的更新。
import tensorflow as tf #创建变量 w = tf.Variable(<initial-value>, name=<optional-name>) #将变量作为操作的输入 y = tf.matmul(w, ...another variable or tensor...)
z = tf.sigmoid(w + y) #使用 assign 或 assign_xxx 方法重新给变量赋值
w.assign(w + 1.0) w.assign_add(1.0)
TensorFlow变量使用流程
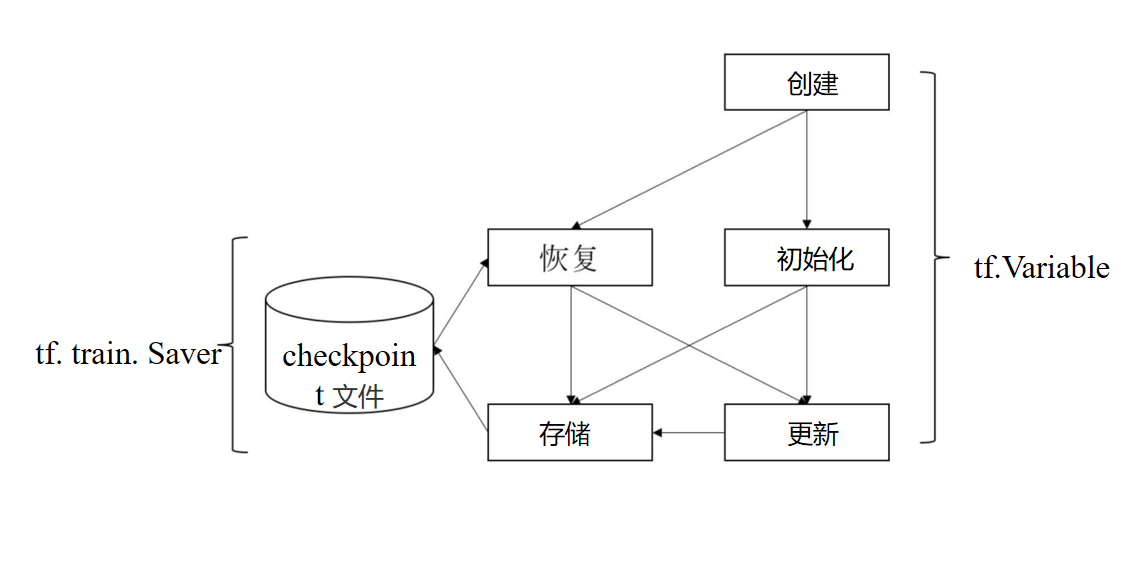
测试代码:
import tensorflow as tf # 创建变量 # tf.random_normal 方法返回形状为(1,4)的张量。它的4个元素符合均值为100、标准差为0.35的正态分布。 W = tf.Variable(initial_value=tf.random_normal(shape=(1, 4), mean=100, stddev=0.35), name="W") b = tf.Variable(tf.zeros([4]), name="b") [W, b] Out[13]: [<tf.Variable 'W_1:0' shape=(1, 4) dtype=float32_ref>, <tf.Variable 'b_1:0' shape=(4,) dtype=float32_ref>] # 初始化变量 # 创建会话(之后小节介绍) sess = tf.Session() # 使用 global_variables_initializer 方法初始化全局变量 W 和 b sess.run(tf.global_variables_initializer()) # 执行操作,获取变量值 sess.run([W, b]) Out[14]: [array([[99.955734, 99.90368 , 99.51574 , 99.51237 ]], dtype=float32), array([0., 0., 0., 0.], dtype=float32)] # 执行更新变量 b 的操作 sess.run(tf.assign_add(b, [1, 1, 1, 1])) # 查看变量 b 是否更新成功 sess.run(b) Out[15]: array([1., 1., 1., 1.], dtype=float32) # ### Saver 使用示例 # ```PYTHON # v1 = tf.Variable(..., name='v1') # v2 = tf.Variable(..., name='v2') # # 指定需要保存和恢复的变量 # saver = tf.train.Saver({'v1': v1, 'v2': v2}) # saver = tf.train.Saver([v1, v2]) # saver = tf.train.Saver({v.op.name: v for v in [v1, v2]}) # # 保存变量的方法 (指定会话, 文件名前缀, 步数) # tf.train.saver.save(sess, 'my-model', global_step=0) # ==> filename: 'my-model-0' # ``` # 创建Saver saver = tf.train.Saver({'W': W, 'b': b}) # 存储变量到文件 './summary/test.ckpt-0' saver.save(sess, './summary/test.ckpt', global_step=0) Out[17]: './summary/test.ckpt-0' # 再次执行更新变量 b 的操作 sess.run(tf.assign_add(b, [1, 1, 1, 1])) # 获取变量 b 的最新值 sess.run(b) Out[18]: array([2., 2., 2., 2.], dtype=float32) # 从文件中恢复变量 b 的值 saver.restore(sess, './summary/test.ckpt-0') # 查看变量 b 是否恢复成功 sess.run(b) Out[21]: array([1., 1., 1., 1.], dtype=float32) # 从文件中恢复数据流图结构 # tf.train.import_meta_graph
• 操作(Operation )是什么
TensorFlow用数据流图表示算法模型。数据流图由节点和有向边组成,
每个节点均对应一个具体的操作。因此,操作是模型功能的实际载体。
数据流图中的节点按照功能不同可以分为3种:
- 存储节点:有状态的变量操作,通常用来存储模型参数;
- 计算节点:无状态的计算或控制操作,主要负责算法逻辑表达或流程控
- 数据节点:数据的占位符操作,用于描述图外输入数据的属性。
操作的输入和输出是张量或操作(函数式编程)
TensorFlow典型计算和控制操作

TensorFlow占位符操作
TensorFlow使用占位符操作表示图外输入的数据,如训练和测试数据。
TensorFlow数据流图描述了算法模型的计算拓扑,其中的各个操作
(节点)都是抽象的函数映射或数学表达式。
换句话说,数据流图本身是一个具有计算拓扑和内部结构的“壳“。在
用户向数据流图填充数据前,图中并没有真正执行任何计算。
# x = tf.placeholder(dtype, shape, name) x = tf.placeholder(tf.intl6, shape=(), name="x") y = tf.placeholder(tf.intl6, shape=(), name="y") with tf.Session{) as sess: #填充数据后,执行操作 print(sess.run(add, feed_dict={x: 2, y: 3})) print(sess.run(mul, feed_dict={x: 2, y: 3}))
测试代码:
In [1]: import tensorflow as tf In [2]: # 常量操作 a = tf.constant(2) b = tf.constant(3)
In [3]: # 创建会话,并执行计算操作 with tf.Session() as sess: print("a: %i" % sess.run(a)) print("b: %i" % sess.run(b)) print("Addition with constants: %i" % sess.run(a + b)) print("Multiplication with constants: %i" % sess.run(a * b)) a: 2 b: 3 Addition with constants: 5 Multiplication with constants: 6 In [4]: # 占位符操作 # x = tf.placeholder(dtype, shape, name) x = tf.placeholder(tf.int16, shape=(), name="x") y = tf.placeholder(tf.int16, shape=(), name="y") In [5]: # 计算操作 add = tf.add(x, y) mul = tf.multiply(x, y) In [6]: # 加载默认数据流图 with tf.Session() as sess: # 不填充数据,直接执行操作,报错 print("Addition with variables: %i" % sess.run(add, feed_dict={x: 10, y: 5})) print("Multiplication with variables: %i" % sess.run(mul, feed_dict={x: 2, y: 3})) Addition with variables: 15 Multiplication with variables: 6 In [7]: # 加载默认数据流图 with tf.Session() as sess: # 不填充数据,直接执行操作,报错 print("Addition with variables: %i" % sess.run(add, feed_dict={x: 2, y: 3})) print("Multiplication with variables: %i" % sess.run(mul, feed_dict={x: 2, y: 3})) Addition with variables: 5 Multiplication with variables: 6
• 会话(Session )是什么
TensorFlow 会话
会话提供了估算张量和执行操作的运行环境,它是发放计算任务的客户端,
所有计算任 务都由它连接的执行引擎完成。一个会话的典型使用流程分为以下3步:

获取张量值的另外两种方法:估算张量 (Tensor.eval ) 与执行操作 (Operation.run )
TensorFlow会话执行

TensorFlow会话执行原理
当我们调用 sess.nm(train_op) 语句执行训练操作时:
• 首先,程序内部提取操作依赖的所有前置操作。这些操作的节 点共同组成一幅子图。
• 然后,程序会将子图中的计算节点、存储节点和数据节点按照 各自的执行设备分类,
相同设备上的节点组成了一幅局部图。
• 最后,每个设备上的局部图在实际执行时,根据节点间的依赖关系将各个节点有序地加载到设备上执行。

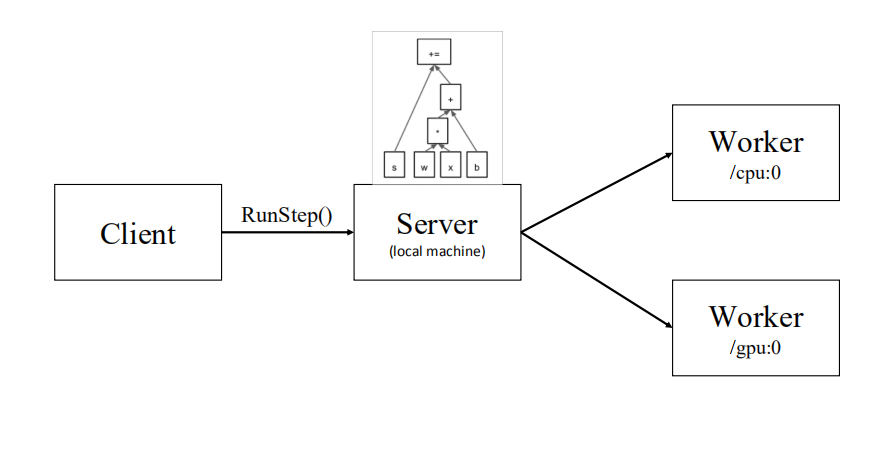
TensorFlow会话本地执行
对于单机程序来说,相同机器上不同编号的 CPU 或 GPU 就是不同的设备,
我们可以在创建 节点时指定执行该节点的设备。

TensorFlow本地计算

测试代码:
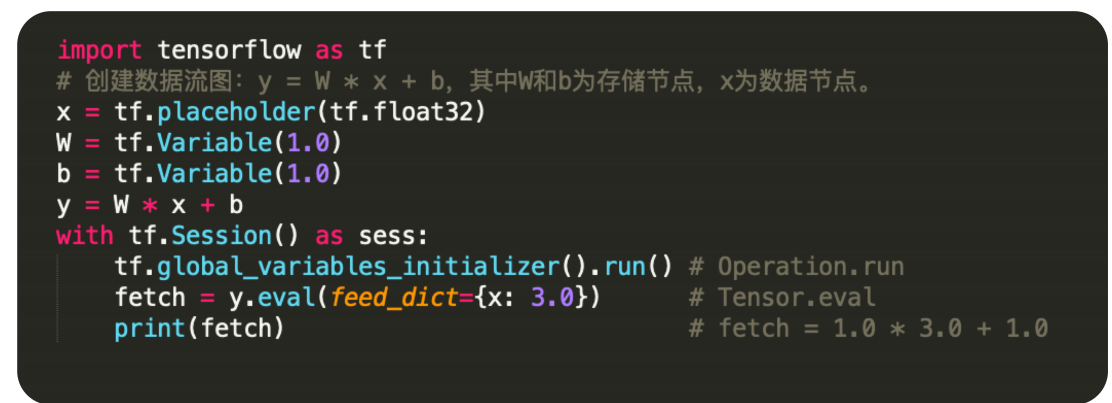
In[1] import tensorflow as tf # 创建数据流图:y = W * x + b,其中W和b为存储节点,x为数据节点。 x = tf.placeholder(tf.float32) W = tf.Variable(1.0) b = tf.Variable(1.0) y = W * x + b with tf.Session() as sess: tf.global_variables_initializer().run() # Operation.run fetch = y.eval(feed_dict={x: 3.0}) # Tensor.eval print(fetch) # fetch = 1.0 * 3.0 + 1.0 4.0
• 优化器( Optimizer )是什么
前置知识:损失函数
损失函数是评估特定模型参数和特定输入时,表达模型输出的推理值与真实值之间不一致程度 的函数。
损失函数L的形式化定义如下:


使用损失函数对所有训练样本求损失值,再累加求平均可得到模型的经验风险。换句话说,
f(x)关于训练集的平均损失就是经验风险,其形式化定义如下:

然而,如果过度地追求训练数据上的低损失值,就会遇到过拟合问题。训练集通常并不能完全
代表真实场景的数据分布。当两者的分布不一致时,如果过分依赖训练集上的数据,
面对新数 据时就会无所适从,这时模型的泛化能力就会变差。
模型训练的目标是不断最小化经验风险。随着训练步数的增加,经验风险将逐渐降低,模型复杂度也将逐渐上升。
为了降低过度训练可能造成的过拟合风险,可以引入专门用来度量模型复杂度的正则化项 ( regularizer ) 或惩罚项( penalty term ) — J(f)。
常用的正则化项有L0、L1 和 L2 范数。因此,我们将模型最优化的目标替换为鲁棒性更好的结构风险最小化 ( structural risk minimization , SRM )。
如下所示,它由经验风险项和正则项两部分构成:
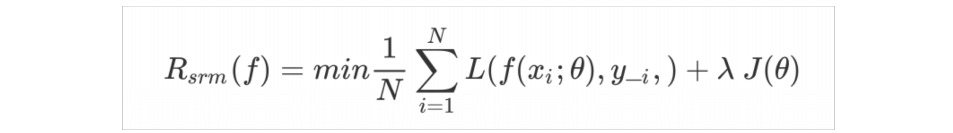
在模型训练过程中,结构风险不断地降低。当小于我们设置的损失值阈值时,则认为此时的模 型已经满足需求。
因此,模型训练的本质就是在最小化结构风险的同时取得最优的模型参数。 最优模型参数的形式化定义如下:

典型的机器学习和深度学习问题通常都需要转换为最优化问题进行求解。
求解最优化问题的算法称为优化算法,它们通常采用迭代方式实现:首先设定一个初始的可行解,
然后基于特定的函数反复重新计算可行解,直到找到一个最优解或达到预设的收敛条件。
不同的优化算法采用的迭代策略各有不同:
• 有的使用目标函数的一阶导数,如梯度下降法;
• 有的使用目标函数的二阶导数,如牛顿法;
• 有的使用前几轮迭代的信息,如Adam。
基于梯度下降法的迭代策略最简单,它直接沿着梯度负方向,即
目标函数减小最快的方向进行直线搜索。其计算表达式如下:

典型的机器学习和深度学习问题,包含以下3个部分:
1. 模型:y=f(x)=wx+b,其中x是输入数据,y是模型输出的推理值,w和b是模型参数,即用户的训练对象。
2. 损失函数:loss=L(y, y_-),其中y_是x对应的真实值(标签),loss为损失函数输出的损失值。
3. 优化算法: w←w+α*grad(w),b←b+α*grad(b),其中 grad(w) 和 grad(b) 分别表示当损失值为loss时,
模型参数w和b各自的梯度值,α为学习率。

优化器是实现优化算法的载体。
一次典型的迭代优化应该分为以下3个步骤:
1. 计算梯度:调用compute_gradients方法;
2. 处理梯度:用户按照自己需求处理梯度值,如梯度裁剪和梯度加权等;
3. 应用梯度:调用apply_gradients方法,将处理后的梯度值应用到模型参数。
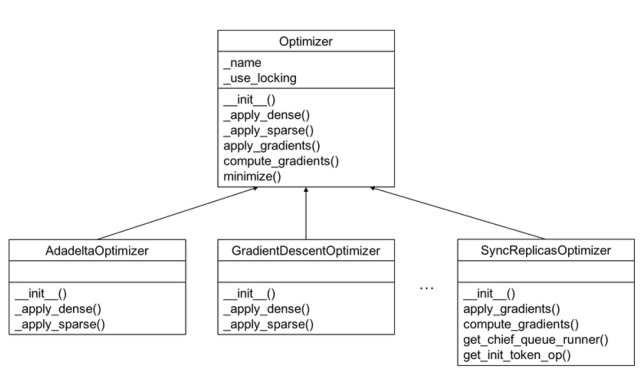

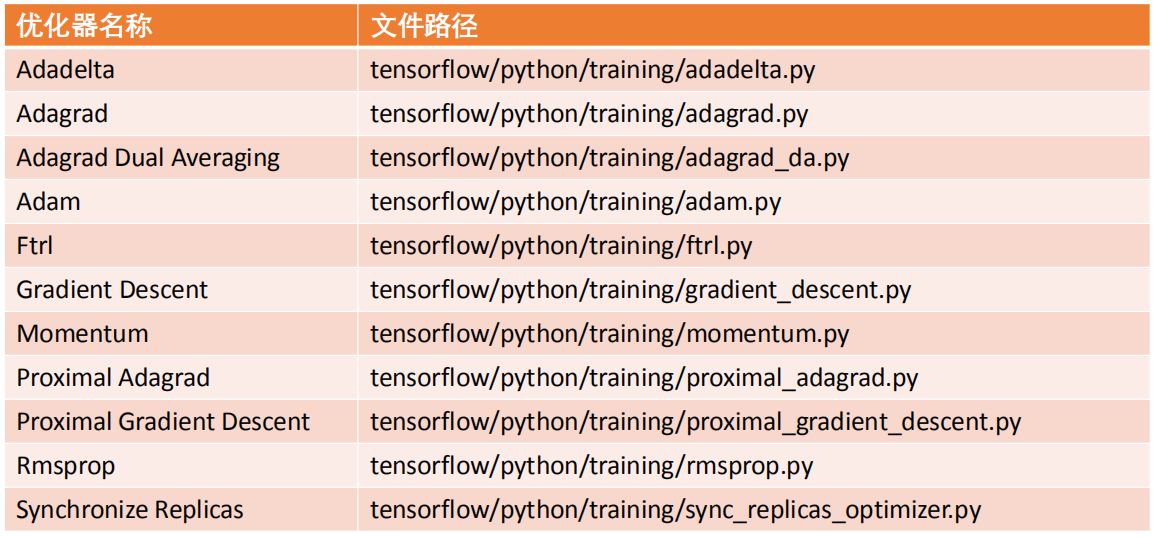
TensorFlow内置优化器
请你一定不要停下来 成为你想成为的人
感谢您的阅读,我是LXL



 浙公网安备 33010602011771号
浙公网安备 33010602011771号