力扣每日一题+python知识点回顾（四）

力扣题目：统计无向图中无法互相到达点对数（题号：2316）

给你一个整数n，表示一张无向图中有n个节点，编号为0到n-1。同时给你一个二维整数数组edges ，其中edges[i]=[ai,bi]表示节点ai和 bi之间有一条无向边。

请你返回无法互相到达的不同点对数目。

示例一：

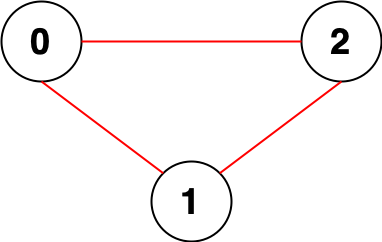
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。

示例二：

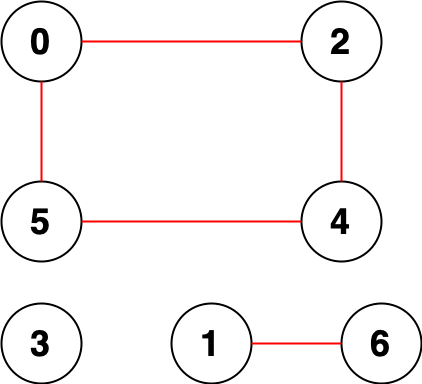
输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

编程思路：深度优先搜索

由于是无向图，我们首先用二维列表保存图，然后使用深度有先搜索的方式，找出每一个连通分量中的节点个数num，然后将当前连通分量的节点个数num与之前连通分量的节点个数总和sum相乘，即可得到当前连通分量中的不可达点对数目，然后将这个数目加到ans中，继续搜索下一个连通分量，直到搜索完所有连通分量，直到搜索完所有连通分量。

编程代码：

class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        ans = sum = 0 # sum计录之前区块的点数
        visit = [False] * n
        for u,v in edges:
            g[v].append(u)
            g[u].append(v)

        def dfs(x: int) -> int:
            visit[x] = True 
            num = 1 #记录当前区块点数
            for y in g[x]:
                if not visit[y]:
                    num += dfs(y)
            return num

        for i in range(n):
            if not visit[i]:
                num = dfs(i)
                ans += sum * num
                sum += num
        return ans