第一章 绪论
1.1数据结构的讨论范畴
Pascal语言的创始人 Niklaus Wirth 教授提出过大名鼎鼎的程序设计公式
Algorithm + Date_Structures = Programs
算法 + 数据结构 = 程序设计
程序设计:为计算机解决问题编制一组指令集
算法 :处理问题的策略
程序设计 :处理问题的数学模型
1.2基本概念
一、数据与数据结构
数据:所有能被输入到计算机中,且被计算机处理的符号的集合,数据本身就是一种集合。也可以说数据是计算机操作对象的总称。
当然也可以理解为计算机处理的信息的某种特定符号的总称。
这里有个理解,显然,这个数据的概念是在扩大的,如果最开始只能处理数字,字符等,那么现在早已能够处理图像 像素等,随着计算机技术的发展,相信这个概念还将继续扩大。
数据元素:上面已经说了数据是一种集合,那必然存在其内部的元素,自然叫做数据元素,对于数据里的单个个体而言,就可以称之为数据元素
数据元素是讨论数据结构的基本单位,但不是最小单位(为什么?)
数据项: 讨论数据结构的最小单位,数据元素是数据项的集合。
例子1:数据元素: 运动员
数据项 : 姓名 俱乐部名称 出生日期 参加日期 职务 业绩
数据项 : 年 月 日(上面的,出生日期,包含多个数据项的的数据项称为组合项)
数据结构:带结构的数据元素的结合,这里的 结构 是指数据元素之间的关系,这种关系我们称之为 逻辑结构。
例子:一个含12位数的十进制数就可以用三个4位的十进制数表示
1234,5678,9101------------>a1(1234), a2(5678),a3(9101)
显然这里的关系就是“次序”,即:a2必须在a1后,a3必须在a2后 <==> <a1, a2>, <a2,a3> (下面表示次序均以右边这种形式表示)
例子:2行3列的二维数组 {a1, a2, a3, a4, a5, a6}
a1 a2 a3
a4 a5 a6
这里的数据元素之间的关系有两个:
1:行的次序关系 row = {<a1, a2>, <a2, a3>, <a4, a5>, <a5, a6>}
2: 列的次序关系 col = {<a1, a4>, <a2, a5>, <a3, a6>}
以上任意一个关系出错,就导致不同的数据结构
数据结构中元素之间的关系,即 逻辑结构 有以下4种
集合:结构中的数据元素除了“同属于一个集合”外,没有其它关系
线性结构:结构中的数据元素之间存在一对一的关系
树型结构:结构中的数据元素之间存在一对多的关系
图状结构或网状结构:结构中的数据元素之间存在多对多的关系
1.3数据结构的定义形式
数据结构的形式定义是一个二元组:
Data-Structure=(D,S)
其中:D是数据元素的有限集,S是D上关系的有限集。
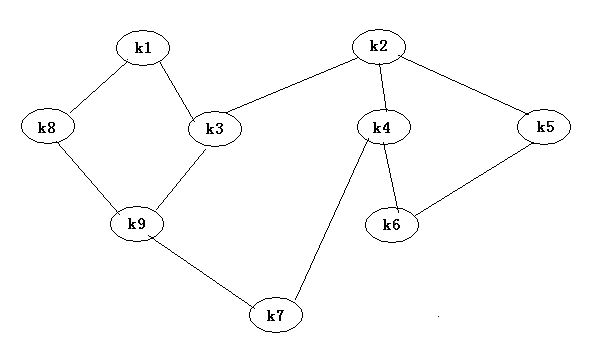
例2:设数据逻辑结构B=(K,R)
K={k1, k2, …, k9}
R={ <k1, k3>,<k1, k8>,<k2, k3>,<k2, k4>,<k2, k5>,<k3, k9>,<k5, k6>,<k8, k9>,<k9, k7>,<k4, k7>,<k4, k6> }
画出这逻辑结构的图示,并确定那些是起点,那些是终点 貌似不是很难,简单!
1.4数据结构的存储方式
前面已将说了,数据结构包括: 数据元素 和 逻辑结构,计算机的操作对象是数据结构,那么必然涉及数据结构的储存




