三角形重心插值颜色填充算法

1.三角形重心插值算法

    三角形是3D图形在渲染时需要处理的基本图元，最终3D图形映射到2D屏幕空间中后需要对三角形进行光栅化渲染。一个简单的光栅化渲染方法是对三角形内部点根据其顶点来进行插值，从而将每个三角形渲染出来。三角形重心插值算法是一种根据重心计算当前点占三个顶点的权重，其公式如下所示。

 

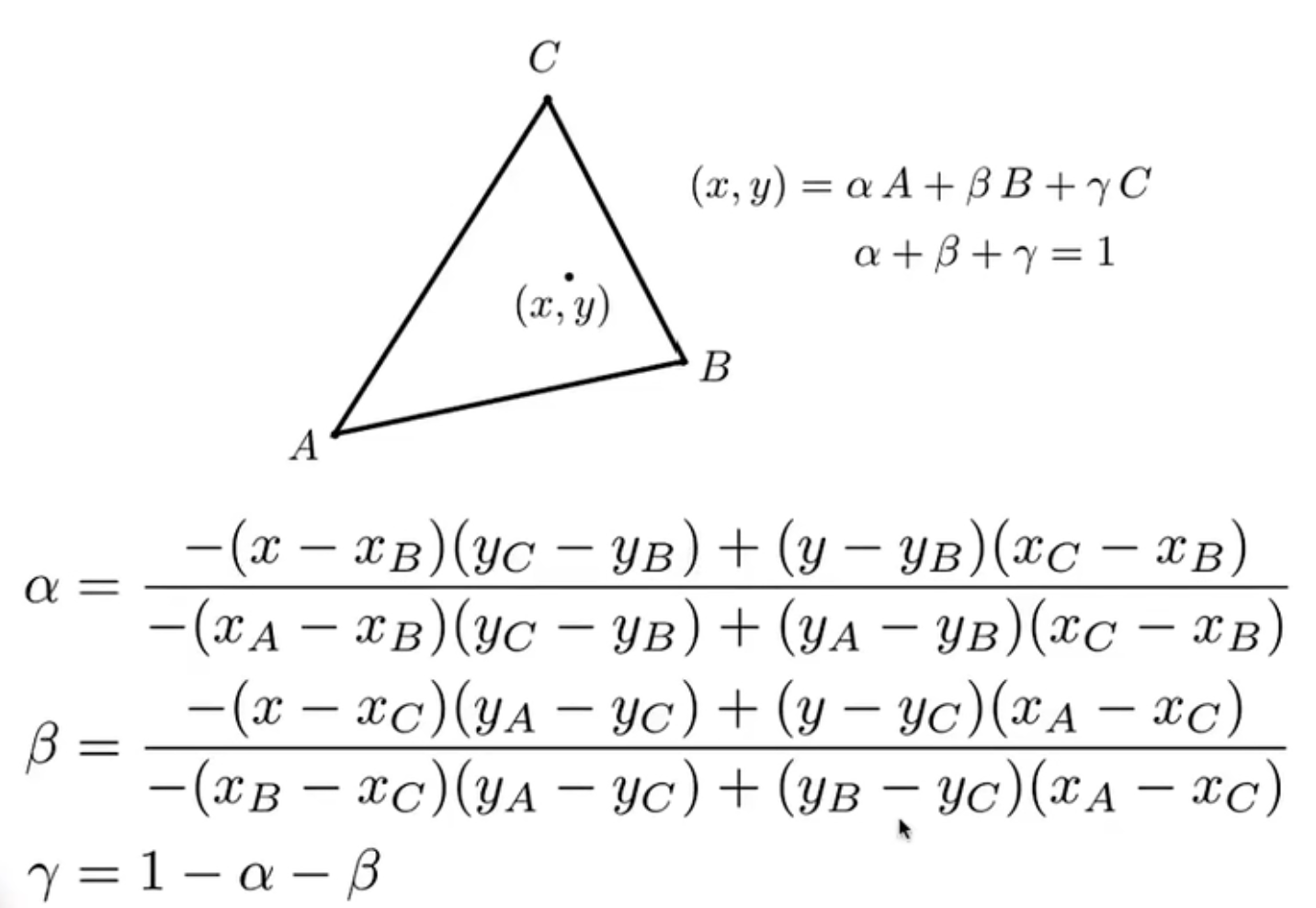
根据上图公式便可计算三角形内部任意一点的插值，这个插值可以是颜色，也可以是其它量，如深度、光照量。

2.三角形颜色填充算法

     为了对三角形颜色按照重心插值进行填充，需要对三角形内的每一点进行遍历，然后根据上图公式求出三个权重值，最后将三个权重作用于三角形的三个顶点A,B,C的颜色，从而达到对三角形进行重心颜色填充的目的。对三角形填充有两种方法，一种方法是先求解三角形的最小外接矩形，然后对矩形内所有点进行扫描，并根据向量叉积来判断当前点是否在三角形内，从而达到填充目的。第二种方法是扫描线法，此方法先将三角形分解为两个平底三角形，然后分别计算水平线与平底三角形的交点，最后使用画线函数来绘制水平线从而对三角形进行填充。由于扫描线法效率相对较高，这里采用扫描线法来对三角形进行填充。

 

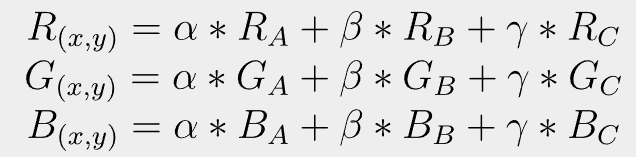
 利用上式便可编三角形颜色填充代码。

void DrawTrangle(SDL_Surface *s,const Point2D p1,const Point2D p2,const Point2D p3)
{
    Point2D ps[3] = {p3,p2,p1};
    /**       p1
               /\
              /  \
             /    \
            /      \
           /        \
          /上半部分  \
         /            \
        p2-------------\ (mid_x,mid_y)
                        \
             下半部分    \
                          \
                           \
                            p3
    */
    /*** 对三角形顶点进行排序， */
    Point2D tmp;
    if(ps[0].y < ps[1].y)
    {
        tmp = ps[0];
        ps[0] = ps[1];
        ps[1] = tmp;
    }
    if(ps[0].y < ps[2].y)
    {
        tmp = ps[0];
        ps[0] = ps[2];
        ps[2] = tmp;
    }
    if(ps[1].y < ps[2].y)
    {
        tmp = ps[1];
        ps[1] = ps[2];
        ps[2] = tmp;
    }

    /** 计算出分割点   */
    int mid_y = ps[1].y;
    int mid_x = ps[2].x -  (int)((ps[2].y - mid_y)*(ps[2].x - ps[0].x)/(ps[2].y - ps[0].y));
    Point2D mid_p;
    mid_p.x = mid_x;
    mid_p.y = mid_y;
    mid_p.color = 0xff;
    /** 获取分割点的插值颜色 */
    GetInterpolationColor(mid_p,ps[0],ps[1],ps[2],mid_p.color);
    /** 绘制两个平底三角形  */
    DrawTop2BottomTrangle(s,mid_p,ps[0],ps[1]);
    DrawBottom2TopTrangle(s,mid_p,ps[2],ps[1]);
}

void DrawTop2BottomTrangle(SDL_Surface *s,Point2D p1,Point2D p2,Point2D p3)
{
    if(p2.y <= p1.y)
        return ;
    Point2D p;
    if(p1.x > p3.x)
    {
        p = p1;
        p1 = p3;
        p3 = p;
    }
    /**        p2
               /\
              /  \
             /    \
            /      \
           /        \
        p1 ---------- p3
    */
    for(int y=p1.y ;y<=p2.y;y++)
    {
        int left_x = p2.x - (int)((p2.y - y)*(p2.x - p1.x)/(p2.y-p1.y));
        int righ_x = p2.x - (int)((p2.y - y)*(p2.x - p3.x)/(p2.y-p3.y));

        for(int x = left_x;x<righ_x;x++)
        {
            Point2D p;
            p.x = x;
            p.y = y;
            /** 进行颜色插值 */
            GetInterpolationColor(p,p1,p2,p3,p.color);
            MySDLPutPixel24_nolock(s,x,y,p.color);
        }
    }
}

void DrawBottom2TopTrangle(SDL_Surface *s,Point2D p1,Point2D p2,Point2D p3)
{
    if(p2.y >= p1.y)
        return ;
    Point2D p;
    if(p1.x > p3.x)
    {
        p = p1;
        p1 = p3;
        p3 = p;
    }
    /**
        p1 ---------- p3
           \          /
            \        /
             \      /
              \    /
               \  /
                \/
                p2
    */
    for(int y=p1.y ;y>=p2.y;y--)
    {
        int left_x = p2.x - (int)((p2.y - y)*(p2.x - p1.x)/(p2.y-p1.y));
        int righ_x = p2.x - (int)((p2.y - y)*(p2.x - p3.x)/(p2.y-p3.y));
        /** 进行颜色插值 */
         for(int x = left_x;x<righ_x;x++)
         {
            Point2D p;
            p.x = x;
            p.y = y;
            /** 进行颜色插值 */
            GetInterpolationColor(p,p1,p2,p3,p.color);
            MySDLPutPixel24_nolock(s,x,y,p.color);
         }
    }
}


void GetInterpolationColor(Point2D p,Point2D p1,Point2D p2,Point2D p3,uint32_t &color)
{
    float x = p.x;
    float i = p.y;
    /** 进行颜色插值 */
    float alph = (-(x-p2.x)*(p3.y-p2.y) + (i-p2.y)*(p3.x-p2.x))/(-(p1.x-p2.x)*(p3.y-p2.y)+(p1.y-p2.y)*(p3.x-p2.x));
    float beta = (-(x-p3.x)*(p1.y-p3.y)+(i-p3.y)*(p1.x-p3.x))/(-(p2.x-p3.x)*(p1.y-p3.y)+(p2.y-p3.y)*(p1.x-p3.x));
    /** 注意RGB是三通道，在计算插值颜色时需要分别计算三个通道的插值分量，最后再合并为的插值颜色 */
    uint32_t pixel_r = (uint32_t)((p1.color&0xff) *alph + (p2.color&0xff)*beta + (p3.color&0xff) *(1-alph-beta));
    uint32_t pixel_g = (uint32_t)(((p1.color&0xff00)>>8) *alph + ((p2.color&0xff00)>>8)*beta + ((p3.color&0xff00)>>8) *(1-alph-beta));
    uint32_t pixel_b = (uint32_t)(((p1.color&0xff0000)>>16) *alph + ((p2.color&0xff0000)>>16)*beta + ((p3.color&0xff0000)>>16) *(1-alph-beta));
    color = pixel_r|(pixel_g<<8)|(pixel_b<<16);
}

然后在主函数种调用即可对给定的三角形进行渲染。

/* initialize SDL video  */
SDL_Surface *surface = MySDL_Init( 200*4, 200*4,0x00);

Point2D p1={.x = 20,.y = 500,.color = 0xff0000};
Point2D p2={.x = 300,.y = 780,.color = 0xff};
Point2D p3={.x = 330,.y = 500,.color = 0xff00};

DrawTrangle(surface,p1,p2,p3);
MySDL_UpdateScreen(surface);

 

 

 

三角形填充效果如下。