图论
图论
CF76A Gift
思路
因为有两个变量，所以先按照其中一个 \(g\) 排序，就像图海说的两只鸟先拍死一个再说。
设生成树边集为 \(T\) ，将排序后的边 \(i\) 加入时， \(g_{max}\) 已经确定，所以可以直接将 \(i\) 暴力插入，然后排序求一次最小生成树，将无用的边删去。
时间复杂度 \(O(nm\log n)\)
优化
发现边集 \(T\) 中的边已经按照 \(s\) 升序排列，故直接暴力插入
时间复杂度 \(D(nm)\)
P4180 [BJWC2010] 严格次小生成树
先求出最小生成树，然后做一下倍增，维护最大值和严格次大值。
对于每一条非树边，将其加入图中，删去这条边的两端点到 \(LCA\) 的边的最大边（若最大边边权与非树边相等则删去严格次大值，若没有严格次大值，则跳过此非树边）
最后对新树的边权和求一下最小值，即为所求。
时间复杂度 \(O(m\log n)\)
CF1076D Edge Deletion
前置：最短路径树
不妨直接从 \(1\) 开始跑 \(DJSL\) ，边跑边生成最短路径树，直到边数大于 \(k\) 或者 \(DJSL\) 跑完了 退出就可以了。
CF1108F MST Unification
在这里哦
CF1650G Counting Shortcuts
前置：分层图
呜呜呜，这个题的题干不知怎么了，看错了好多次，QWQ
我们将图按照距离分层，发现如果是最短的话，那么路径上只会有从 \(i层->i+1层\) 的路径，而如果是次短的话，就回恰好有一条在同一层内的路径。
所以设 $dp_{i,0/1} $ 表示到 \(i\) 的最短路径数量和次短路径数量
对于一条同层边 \((u,v)\) 有 \(dp[v][1]+=dp[u][0]\)
对于一条跨层边 \((u,v)\) 有 \(dp[v][1]+=dp[u][1]，dp[v][0]+=dp[u][0]\)
发现 \(dp[v][1]\) 可能在需要被转移时还没有算完，于是先算同一层的 \(dp[v][1]\) 再算跨层的 \(dp[v][1],dp[v][0]\)
CF1737D Ela and the Wiring Wizard
在这里哦
P2149 [SDOI2009] Elaxia的路线
正解还没看呢，唔，手上只有一个自己写的 \(n^3\) 玄学算法A掉了这个题。
大概就是将两组最短路算出来，然后先将第一个人的最短路的边全部处理出来，处理出其中的每一个点到之前的点的距离。
对于第二组，也是先找一个最短路的边。对于一个点，处理出可以到达这个点的最短路上的点，然后看在第一个人处理出来的距离中有没有这两个点，然后取个最大值即可。
注意哦，以上都为单向边。
正解的话，先鸽了吧。
P1341 无序字母对
前置：欧拉路
巧了，这个前置我似乎不会，等我学学。
嗯，好了，可能会了，开始吧！
直接将两个字母连边，然后先判是否有欧拉路
判断方法：
-
无向图欧拉路
其中度数为奇数的点的数量不是 \(0\) 就是 \(2\) ，否则无解。
如果为 \(2\) 则这两点之一取小的作为起点
-
有向图欧拉路
图中恰好存在 \(1\) 个点出度比入度多 \(1\)（这个点即为 起点 \(S\)），\(1\) 个点入度比出度多 \(1\)（这个点即为 终点 \(T\)），其余节点出度=入度。
-
有向图欧拉回路
所有点的入度=出度
-
无向图欧拉回路
所有点的度数都是偶数
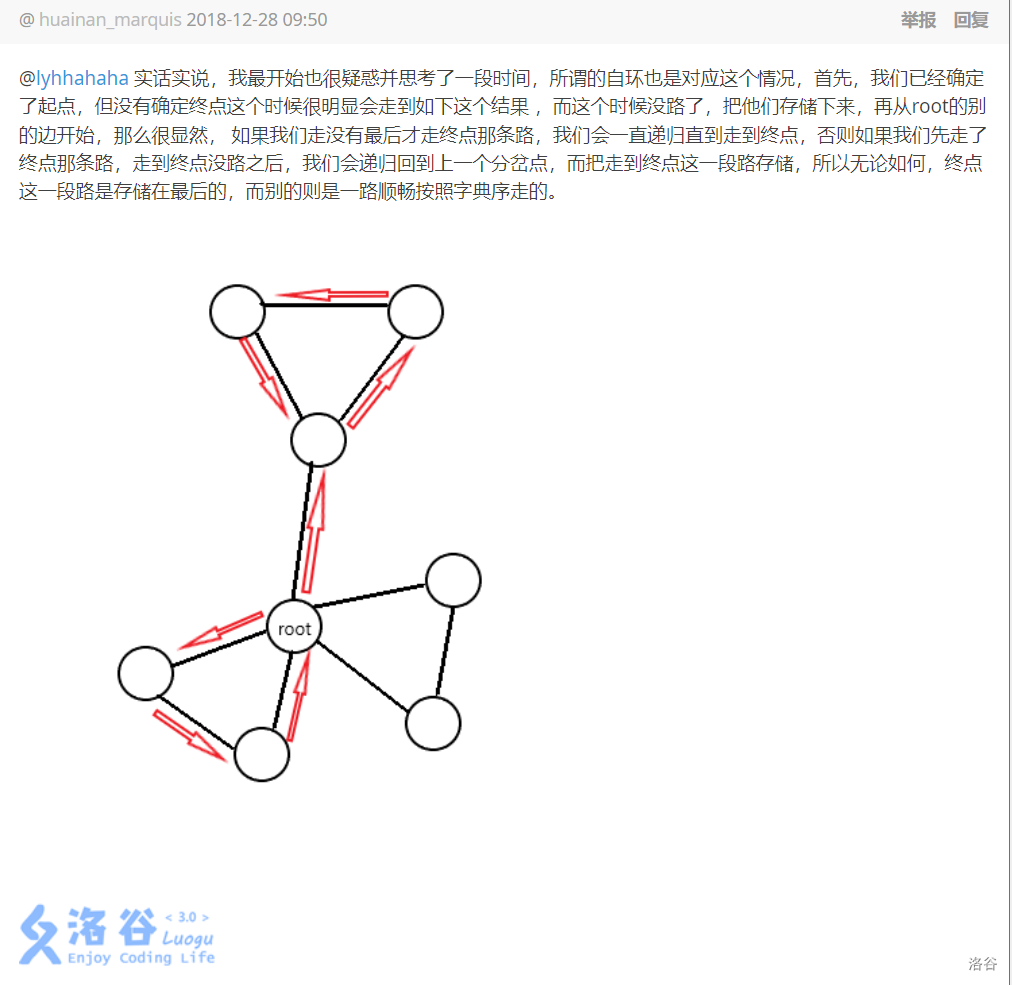
注意一下记录答案，必须要倒序，在这里有详解，再此感谢$dalao $$@huainan_marquis $
P8201 [传智杯 #4 决赛] 生活在树上（hard version）
思路
可以发现，如果在 \(a,b\) 间的简单路径上有一个点的点权为 \(dis_{a,b} ⨁ k\) ，则成立，反之则不存在这种点。
于是问题转化：问树上 \(a,b\) 简单路径上是否有点的点权为 \(C\)
这是一个经典问题，对点权离散化，将询问离线到 \(a,b,lca(a,b)\) 上，开个桶记录一下就可以了。
注意，如果 \(lca(a,b)\) 的点权为 \(C\) 的话，要特判一下。
CF427C Checkposts
大水题，只用记录一下每个环里面最小值和其对应的点的个数即可
所以一个 \(tarjan\) 和乘法原理即可
