基环树
基环树
一.前言
由于某人考试时，发现有基环树的题目，但不知道怎么写。
于是发挥奇思妙想，将环特意固定为非根节点，成功地，2.5小时（年） 没写出来。
于是痛定思痛，认真学习。
二.定义
基环树
有 \(n\) 条边 \(n\) 个点的连通图，可以被称为基环树。
其有无向图，有向图两种，其中有向图有特殊两种情况：外向图（仅有一条入边）以及内向图（仅有一条出边）。
- 基环树
-
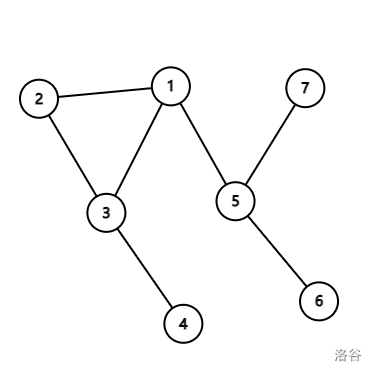
外向基环树
-
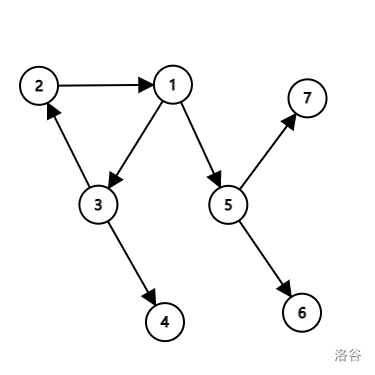
内向基环树
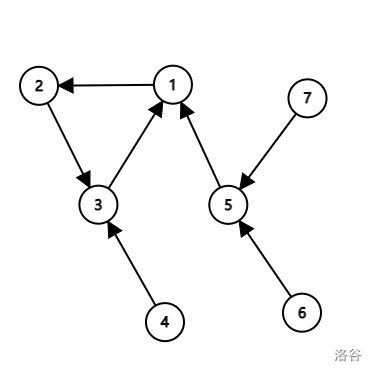
基环树森林
由基环树构成的森林，也满足只有 \(n\) 个点 \(n\) 条边。
基本做题思路
将环看作一个大节点，作为树根，将其按照一般树上问题去考虑。
然后再考虑环上的贡献
三.例题
P4381 [IOI2008] Island
基环树+单调队列DP+直径
坑点：
long long- 最长路径不过环上的情况
- 一个环只有 \(2\) 个点
- 每个连通块只可以取一条路径
思路
-
最长路径过环
考虑单独的一颗基环树，将其的环作为树根，去找以环上某个点为根节点的子树最大深度 \(dep_i\) 。
套路： 将环破坏成链，并复制，求出 \(dep_i+dis_{i,j}+dep_j\) 的最大值，若直接 \(DP\) 则为 \(O(n^2)\) 考虑 \(DDQ\) （单调队列），将其优化为 \(O(n)\)
-
最长路径不过环
注：路径不过环，是指没有环上的边，而非没有环上的点
对于每一个最大无环子树取其直径即可
然后就完了，嗷呜QWQ
信息学的尽头 (end)
题目描述
人们建立了 \(n\) 组计算集群，并给了这些它们 \(1\) 到 \(n\) 的编号。这些计算集群之间有共 \(n\) 条双向通信通道，将它们连接成一个连通的网络。每条双向通道都有一定的延迟。一族信息可以经过若干条首尾相接的通信通道被传递，产生的延迟为其经过的所有通道的延迟之和。
王五负责协调计算集群之间的通信。他需要对于每个计算集群，计算其向所有其它计算集群发送一族信息所需产生的最小延迟之和。如此艰巨的任务，他自然就分配给了亘古通今至高无上万年超级大码农——你。
输入格式
第一行一个整数 \(n\)。
接下来 \(n\) 行每行三个正整数 \(u,v,w\)，表示 \(u\) 号计算集群与 \(v\) 号计算集群间有一条延迟为 \(w\) 个单位的通信通道。
输出格式
一行 \(n\) 个整数，第 \(i\) 个数表示 \(i\) 号计算集群的答案。
样例
输入样例 #1
3
1 2 3
2 3 2
1 3 1
输出样例 #1
4 5 3
输入样例 #2
4
1 2 3
2 3 2
3 4 1
4 1 4
输出样例 #2
12 8 8 8
数据范围及约定
对于 \(30\%\) 的数据：\(3 \le n \le 200\)；
对于 \(60\%\) 的数据：\(3 \le n \le 2000\)；
对于 \(100\%\) 的数据：\(3 \le n \le 200000\)，\(1 \le w \le 1000\)，\(1 \le u,v \le n\)。保证两两计算集群之间被通信通道连通，保证两计算集群间不会有多条通信通道，保证不存在通信通道的起点终点相同。
思路
换根DP+基环树+双指针
- 首先以环为根，求得以环上节点为根的子树，走到环上的延迟。
- 其次求得环上节点的答案，破环为链复制一遍，考虑一个双指针 \(l,r\) 使得 \([l,r]\) 之间的所有节点都为顺时针到达节点 \(l\) 其余为逆时针，由此来 \(O(n)\) 算贡献即可。
- 然后换根DP，考虑一个节点 \(u\) 与其父亲节点 \(v\) ，假设其父亲节点已经求出了题目所求，易得 \(dp[u]=dp[v]-(n-2*siz[u])*dis_{u,v}\) 因为只用考虑他们相连的边所产生的贡献即可。
P1399 [NOI2013] 快餐店
思路
这个题的问题转化为，将环上一点删去，使得树的直径最小。答案就是 \(直径/2.0\) 。
同之前，我们考虑直径不在环上的情况，得到最大直径 \(ans_1\) ，并将每个子树的最大深度 \(dep\) 算出来。
关键： \(O(n)\) 求得直径最小值
我们破环为链，设得到的链为 \(\{a_1,a_2,a_3,....,a_{top} \}\)
这里相当于将 \(a_1\) 与 \(a_{top}\) 断开，所以记 \(L=dis{a_1,a_{top}}\)
令 \(A[i]\) 表示从第一个点向后到达 \(a_i\) 经过的点中（包括 \(a_i\) ）\(\max(dis_{a_1,a_j}+dep_{a_j})\)
令 \(B[i]\) 表示从第 \(top\) 个点向前到达 \(a_i\) 经过的点中（包括 \(a_i\) ）\(\max(dis_{a_{top},a_j}+dep_{a_j})\)
令 \(C[i]\) 表示在 \([a_1,a_i]\) 这几个点及其子树单独抽出来所构成的树的直径的最大值（不考虑子树直径，即强制直径过环）
令 \(D[i]\) 表示在 \([a_i,a_{top}]\) 这几个点及其子树单独抽出来所构成的树的直径的最大值（不考虑子树直径，即强制直径过环）
所以 \(ans_2=\min(\max(C[i],C[i+1]),A[i]+B[i+1]+L)\)
所以 \(\max(ans_1,ans_2)/2.0\) 即为所求。
这个转移方程的意思是：
此时，将 \(a_i,a_{i+1}\) 这条边断开，求得的直径为多少。这里，贡献有三个部分构成：
- 在 \(a_i\) 到 \(a_1\) 中出现直径
- 在 \(a_{i+1}\) 到 \(a_{top}\) 中出现直径
- 直径经过 \(a_1,a_{top}\) 这条边
后记
呜呜呜，写了三节晚自习都没写出来，嗷呜
细节众多
CF835F Roads in the Kingdom
同上，但是，注意数据中出现的只有一个环的情况，可能会出错，建议特判。
