浅谈DP

DP

定理

一个定理（不知道叫啥名）

用途：解决石子合并最大值问题

结论：当要合并 $[i,j]$ 区间时，其最大值有两种情况：

先合并 $[i,j-1]$ ，再加上 $j$
先合并 $[i+1,j]$ ，再加上 $i$
前提：所有数为正数

证明：

FUCK_CCF

四边不等式

定义

设 $w(x,y)$ 是定义在整数集合上的二元函数，若对于定义域上的任意整数 $a,b,c,d$ ，满足 $a<b<c<d$ ，都有： $w(a,c)+w(b,d)>w(a,d)+w(b,c)$ ，则称函数 $w(x,y)$ 满足四边不等式。

用途

区间动规优化（最小值）

对于一个问题有 $n^2$ 个状态，每个状态有 $n$ 种决策（老姚称之为 $2D1D$ ），动态转移方程形似如下：

$dp_{i,j}=\min_{k=i}^{j-1}(dp_{i,k}+dp_{k+1,j})+w(i,j)$
直接简单地转移为 $O(n^3)$ ，当 $w(l,r)$ 满足某些性质时，我们可以利用决策的单调性进行优化

区间包含单调性： 对于任意的 $l<=l'<=r'<=r$ ，满足 $w(l',r')<=w(l,r)$

四边形不等式： 对于任意的 $l<=l'<=r'<=r$ ，满足 $w(l,r')+w(l',r)<=w(l,r)+w(l',r')$ ，若等号恒成立，则称之为四边恒等式

引理1： 若 $w(i,e)$ 满足区间包含单调性和四边形不等式，则状态 $dp_{i,e}$ 满足四边形不等式。

引理2： 若状态 $f$ 满足四边形不等式，记 $S_{i,j}$ 为 $dp_{i,j}$ 的最优决策点，则有：

$S_{l,r-1}<=S_{l,r}<=S_{l+1,r} ~~ (l+1<r)$
注：对于 $S_{i,i}$ ，可以认为其最优决策点为 $i$

证明详见

$Dilworth$ 定理

结论：偏序集的最少反链划分数等于最长链的长度。
人话版的结论：

若要将序列 $a$ 划分成 $n$ 个上升子序列，使 $n$ 最小，那么这个 $n$ 就必然等于最长不上升子序列的长度。

因为上升子序列与不上升子序列互为反链

状压DP

CF8C Looking for Order

状态很简单，主要是更新方式。

如果先枚举未更新的，再枚举完成更新的，那么时间复杂度为 $O(n^2*2^n)$

如果枚举完成更新再枚举未更新的，那么时间复杂度 $O(n*2^n)$

具体实现：

当枚举到状态 $i$ ，不妨固定其第一个没拿到的为当前第一个拿的
然后向上更新一次。
之后再用暴力枚举第二个拿的，向上更新即可。
可以证明，这样更新一定会将所有状态更新：因为对于状态 $a$ 你一定可以构造出一个被更新的上一个状态。

最小斯坦纳树

P6192 【模板】最小斯坦纳树

状态转移方程：

\begin{aligned} d p [i] [s] = m i n (d p [i] [s], d p [i] [t m e] + d p [i] [s \otimes t m e]) \\ d p [j] [s] = m i n (d p [i] [s] + v (i, j), d p [i] [s]) \end{aligned}

$\begin{align} \notag &dp[i][s]=min(dp[i][s],dp[i][tme]+dp[i][s\otimes tme])\\ \notag &dp[j][s]=min(dp[i][s]+v(i,j),dp[i][s]) \end{align}$

第二个满足三角形（最短路）不等式，而且有后效性，所以用 $SPFA$ 或者 $DJSL$

$tme$ 代表 $s$ 的一个子集

使用for(int i=s&(s-1);i;i=s&(i-1))遍历子集

P3264 [JLOI2015]管道连接

斯坦纳树森林

首先定义 $dp[i][j]$ 同上

再定义 $ans[i]$ 表示：再关键点状态为 $i$ 的情况下的最小答案，这个关键点状态必须满足：要么将某个颜色全部包含，要么就不包含这个颜色。

\begin{aligned} (1) & a n s [i] = m i n (a n s [i], a n s [j] + a n s [i \otimes j]) \end{aligned}

$\begin{align} ans[i]=min(ans[i],ans[j]+ans[i\otimes j]) \end{align}$

[WC2008]游览计划

这个是最小斯坦纳树输出方案，直接对于每一个状态添加一个 $pre$ 即可。

最后输出的时候用DFS递归处理。

分数DP

基本思想

对于一件物品，有 $w,v$ 这两中参数。从 $n$ 个这种物品，从其中选择 $k$ 个，求出$ \frac{\sum\limits_{i=1}^{{k}{w_i}}{\sum\limits_{i=1}}{v_i}} $ 的最大值。

我们设答案为 $ans$ ，那么就有：

\frac{\sum_{i = 1}^{k} w_{i}}{\sum_{i = 1}^{k} v_{i}} <= a n s

$\frac{\sum\limits_{i=1}^{k}{w_i}}{\sum\limits_{i=1}^{k}{v_i}} <=ans\\$

移项得到：

\sum_{i = 1}^{k} w_{i} - a n s \times \sum_{i = 1}^{k} v_{i} <= 0

$\sum\limits_{i=1}^{k}{w_i}-ans\times\sum\limits_{i=1}^{k}{v_i} <= 0$

变换得到：

\sum_{i = 1}^{k} (w_{i} - a n s \times v_{i}) <= 0

$\sum\limits_{i=1}^k(w_i-ans\times v_i)<=0$

这样我们就可以通过二分 $ans$

对于每一个物品算出的 $w_i-ans\times v_i$ ，再猛贪心排个序，取前 $k$ 个即可。

例题

P4377 [USACO18OPEN] Talent Show G

01分数DP

二分的check函数中，用 $01$ 背包处理。

注意：转移方程比较牛马 $dp[i]!=0,dp[min(i+w,W)]=max(dp[min(i+w,W)],dp[i]+w_i- ans \times v_i)$

就是说，当前这个 $dp[i]$ 必须要被更新过。

P1642 规划

树上分数DP

先转化一下，将 $m$ 个要被删除的点改为，要被连通的 $n-m$ 个点。

二分 $ans$ ，先算出每个工厂的贡献，再 $DP$ 一下即可。

$dp[i][j]=max(dp[i][j],dp[e][j-k]+dp[i][k])+w_i-ans\times v_i$

之后再看有没有一个点 $dp[i][n-m]>=0$ 即可。

P2868 [USACO07DEC]Sightseeing Cows G

最佳比率环

我们要寻找一个环（ $点数=边数$ ），使得其点权（ $v$ ）与边权 $w$ 之比最大。

即求出一个环，使得 $\frac{\sum\limits v_i} {\sum\limits w_i}$ 最大。

根据分数 $DP$ 的惯用手法可得：

\frac{\sum v_{i}}{\sum w_{i}} <= m i d

$\frac{\sum\limits v_i} {\sum\limits w_i}<=mid$

推得：

\sum (v_{i} - w_{i} \times m i d) <= 0

$\sum\limits( v_i -{w_i}\times mid) < = 0$

\sum (w_{i} \times m i d - v_{i}) >= 0

$\sum\limits( {w_i}\times mid - v_i ) > = 0$

所以不妨将一条边的边权改为 ${w_i}\times mid - v_i$ 其中 $v_i$ 代表边的出发点。

然后判断负环：如果有，则证明 $mid$ 小了，反之则 $mid$ 大了。

P4322 [JSOI2016]最佳团体

树上分数DP（依赖背包）

是 $P1642$ 的加强版，常数小大，卡卡常可以过。

当然还是有点区别，这个必须以节点 $0$ 为根。意思是说只可以用 $dp[0][k] ~ ? ~ 0$ 来判断二分。

P3199 [HNOI2009]最小圈

最佳比率环

思路其实差不多，但是要弄清楚是有一个环满足条件还是所有环都满足条件。

顺便在这里证明一个玩意儿：

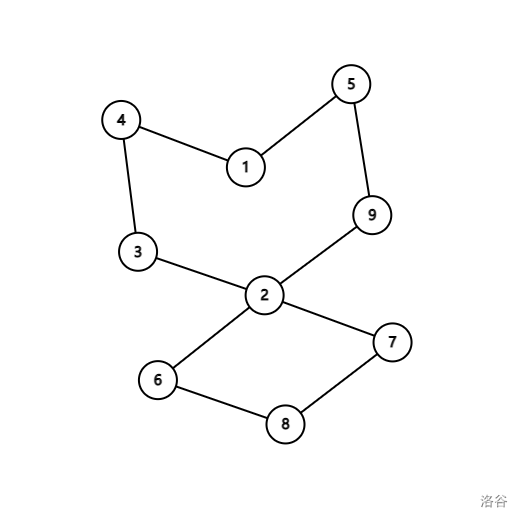
对于这样一张图，走 $4-3-2-6-8-7-2-9-5-1$ 这条路径平均值一定比走 $2-6-8-7$ 或 $4-3-2-9-5-1$ 低。

树形DP

P1131 [ZJOI2007] 时态同步

个人认为本题除了long long之外，就不值一提。

P2016 战略游戏

状态： $dp[i][1/0]$ 表示控制以 $i$ 为根的子树所需的最小侍卫， $0/1$ 表示在 $i$ 处是 $(1)$ 否 $(0)$ 有守卫

转移方程：

$dp[i][1]=\sum \limits_u \min(dp[u][1],dp[u][0])+cost[i]$

$dp[i][0]=\sum\limits_u dp[u][1]$

Vijos P1144 小胖守皇宫

本题与上题不同在于一个是守边，一个是守点

即若一个边被守住了，那一定代表其端点被守住了，但一个点被守住了，不一定代表其连接的边被守住了。所以两个问题不等价。

状态： $dp[i][1/2/3]$ 表示第 $i$ 个点，及其子树被守住所花费的最小代价， $1/2/3$ 表示第 $i$ 个点的守护状态，即被自己，儿子，父亲守护。

转移方程：

$dp[i][1]=\sum \min(dp[u][1],dp[u][2],dp[u][3])+cost[i]$

$dp[i][2]=\sum\min(dp[u][1],dp[u][2])+K$

注：因为被儿子保护，只需要一个 $\min(dp[u][1],dp[u][2])=dp[u][1]$ 即可，即只用一个儿子保护父亲，如果没有这样的儿子，则记录 $K=min(dp[u][1]-dp[u][2])$ 使得强行选择一个儿子保护父亲

$dp[i][3]=\sum \min(dp[u][1],dp[u][2])$

一般线性DP

P1070 [NOIP2009 普及组] 道路游戏

设工厂编号为 $0$ ~ $n$ ，道路编号为他所到达的点的编号。
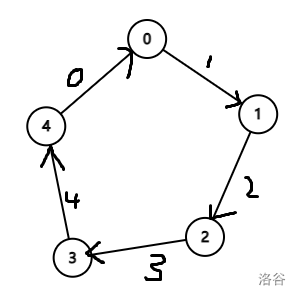
设在第 $i$ 个单位时间时，在第 $j$ 条道路上出现金币的个数为 $money[i][j]$ ，第 $i$ 个工厂的机器人费用为 $cost[i]$
设当行走了 $j$ 个单位时间时，走到第 $i$ 个工厂，所可以得到的金币为 $sum[i][j]$ ，易得 $sum[i][j]=sum[(i-1+n)\mod n][j-1]+money[j][i]$ 。由此我们便可以轻松得出，用 $k$ 个单位时间，在第个单位时间时，走到第个工厂所得到的金币： $sum[j][i]-sum[(j-k+n)\mod n][i-k]$
设在第 $i$ 个单位时间时，得到的金币最大值为 $DP[i]$

易得到：

$DP[i]=max(DP[i-k]+sum[j][i]-sum[j-k][i-k]-cost[j-k])$

化简可得：

$DP[i]=sum[j][i]+max(DP[i-k]-sum[j-k][i-k]-cost[j-k])$

可以看出： $DP[i-k]-sum[j-k][i-k]-cost[j-k]$ 可以用优先队列（单调队列也可以）维护

即设 $rest[j][i]=DP[i-k]-sum[j-k][i-k]-cost[j-k]$

细节1：对于每一个 $rest[j][0],rest[j+1][1],,,rest[j+k][k]$ 用一个优先队列维护，及时排除过时元素。

P1099 [NOIP2007 提高组] 树网的核

这个可能不算一个DP题

前置芝士

对于一个在树上的点来说，其在树上可以到达的最远距离必定是树的直径的端点之一。
$O(n)$ 求直径的方法

将题目翻译成人话

给出一棵树，然后找到其直径，在直径上取一段长度不超过 $s$ 的线段，求出所有点到这条线段的距离的最大值。求这个距离的最小值。

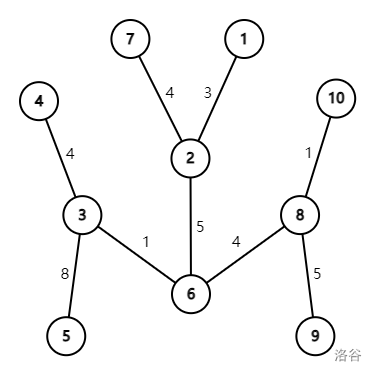
这里会有一个疑问：如果有两条直径怎么办？

不妨看上图：直径分别是 $53627,53689$

不难发现，在只考虑直径的情况下，两条直径关于 $6$ 对称，然而我们只关心最大距离，由前置芝士以及讨论可知，算两条直径和算一条直径的效果是一样的。

主题思想

由前置芝士可得，答案的贡献由两个部分组成：选择线段的端点到直径的距离+被选择的线段上的点不经过直径可以走的最长距离。
枚举起点，贪心可得尽量让线段长，所以尽可能选择多得点更新答案即可。

P1108 低价购买

总结：最长上升子序列+输出方案数

解法一：题解 $O(n^2)$

设 $f[i]$ ， $t[i]$ 分别为以第 $i$ 个数结尾的最长下降子序列长度以及方案数。

所以在 $j[i]>a[i]$ 时可以得到：

当 $f[i]+1>f[j]$ 时， $t[i]=t[j]$
当 $f[i]+1=f[j]$ 时， $t[i]+=t[j]$

重复情况处理：显然，当两个价格重复时，保留后面一个一定更优。

解法二：个人玄学解法 $O(n\log n + ?)$

先用一个二分优化的最长下降子序列

然后对于每一条序列建图，最后记忆化搜索即可。

建图方法：

设以第 $i$ 个数结尾的最长长度为 $Len_i$

将所有最长长度为 $j$ 的点放在集合 $S_j$ 里

设最长长度为 $top$ ，设一个超级原点连接所有在 $S_{top}$ 里的点

由集合 $S_j$ 向 $S_{j-1}$ 建边

最后从超级原点开始记忆化搜索即可

对于去重：每个集合内价格不重复即可

不知道为什么比题解跑得快QWQ

可以优化，到 $O(n \log n)$ 但没有写出来QWQ

解法三：树状数组或者二分求最长下降子序列方案数

时间复杂： $O(n\log n)$

二分

不妨将 $low$ 数组（也就是二分数组） $vector$ 数组，将所有长度为 $i$ 的数字全部存在 $low$ 里，根据一般的二分最长下降子序列写法，这个 $low_i$ 一定为递增的。

同时令 $ans_{i,j}$ 表示以 $low_{i,j}$ 结尾的方案数

由此可得当我们新加入一个数 $b$ ，以其结尾的最长下降子序列长度为 $i$ 时，其所对应的方案数为 $ans_{i,j}=\sum\limits_{e=size(low_{i-1})-1}^{low_{i-1,e}>b} ans_{i-1,e}$

为了时间复杂度优秀，将 $ans$ 取一个前缀和也可以，当然这个决策部分也可以用二分优化
树状数组

这个更简单，直接将 $tree$ 改成结构体，其中有两个元素： $h,sum$ 分别表示长度及其所对应的方案数

再重载一下 $+$ ，如下：
```
bool operator < (const tree & a,const tree & b){
    if(a.h==b.h){
        return (tree){a.h,a.sum+b.sum};
    }
    else (tree){max(a.h,b.h),a.h>b.h ? a.sum : b.sum};
}
```
然后其他就差不多了

P1156 垃圾陷阱

这个数据范围太小了，随便写写都可以过

先对数据以时间作为关键字排序

不妨设 $dp[i][j]$ 表示在处理第 $i$ 个物品时，生命值可以撑到第 $j$ 时刻

由定义可得， $j$ 的枚举范围为 $[t[i],10+\sum\limits_{e=1}^{i-1}]$

转移方程如下：

当这个要被吃掉时， $dp[i][j+f[i]]=max(dp[i-1][j])$
不被吃掉时， $dp[i][j]=max(dp[i][j]+h[i])$

输出答案情况：

合法，即当转移方程第二种情况 $dp[i][j]>=D$ 时，即可输出。
不合法

a. $j$ 的枚举范围不合法，输出 $10+\sum\limits_{e=1}^{i-1}$

b.到最后也没有办法到达井口，输出 $10+\sum\limits_{e=1}^{G}$

~~这个蓝题太水了，建议降绿~~

P1169 [ZJOI2007]棋盘制作

悬线法或者单调栈

P1020 [NOIP1999 普及组] 导弹拦截

方一：

假设目前有 $n$ 套系统被开启，对于一个导弹 $a_i$ 只需找到一个拦截高度最小的可以拦截此导弹的导弹拦截系统取拦截，或者新开一个系统（贪心）

方二：

$Dilworth$ 定理

CF1562E Rescue Niwen!

这个题我遇见了两种题面，一种为人话版，一种为有题目背景版，第二个版本是在考试时遇见的，很突然，没有转化过来题面。

所以做这种题目，建议看有背景的，这样可以锻炼一下题目翻译以及转化能力

题意概述

在一个字符串 $S$ 中，寻找一个最长上升子序列，对于这个序列中相邻的两个元素 $S_{l,r},S_{l',r'}$ 满足一下要求：

$l<l'$ 或者 $l=l' ~\&\&~r<r'$
$S_{l,r}<S_{l',r'}$

结论一： 若 $S_{l,r}$ 可以被接在 $S_{l',r'}$ 后面，那么 $S_{l,r+1}$ 也一定可以

结论二： 若 $S_{l,r}$ 比 $S_{l',r'}$ 小，那么 $S_{l,r+k},k\in N^{*}$ 也一定小于 $S_{l',r'}$

结论三： $S_{l,r}<S_{l,r+1}$

由此我们设 $dp[i]$ 表示以 $S_{i,k},k>=i$ 结尾的最长序列

其实这个状态应该为像 $dp[i][j]$ 这样的二维状态，只不过说由于结论三 $dp[i][j]<dp[i][j+1]$ 所以有大量状态不可能被用于更新下一个状态，所以滚掉

我们设 $g_{i,j}$ 以 $S_i,S_j$ 开头的最长公共子串

所以有：

$dp[i]=max(n-i+1,slove(i))$

$slove(i)=max_{j=1}^{i-1}(S_{i+g[i][j]}<=S_{j+g[i][j]}~?~0:n-i-g[i][j]+1)$

CF1699D Almost Triple Deletions

状态定义：

定义 $dp_i$ 表示使得前 $i$ 个合并后，使得其只剩下了 $a_i$ 这一种值的最长长度

所以可以得到 $dp_i=\max \{dp_j+1~(a_i==a_j\&\&can_{j+1,i-1})\}$

其中 $can_{i,j}$ 表示 $[i,j]$ 可以完全被削掉

结论

若有一个区间使得其中的众数的个数不超过区间的一半，且区间为偶区间则这个区间可以完全被削掉

用这个结论可以在 $N^2$ 之内算出 $can$

区间DP

P5569 [SDOI2008] 石子合并

GarsiaWachs算法

我们假设只有三个石子 $a,b,c$ ，由此其的合成方式有二 $(a+b)+a+b+c$ ， $(b+c)+a+b+c$ 易得只用看 $a,c$ 大小即可判断谁更小。

状压DP

CF662C Binary Table

题意简述

给出一个 $01$ 矩阵，每次操作可以将某一行或者一列反转，你可以进行无数次操作，求出矩阵最少可以有多少个 $1$

问题转化

如果我们将最少有多少个转化成不重复的单点反转，那么问题的结局就转化为将矩阵变为 $0$ 矩阵

我们将问题转化成用一下两种操作：

反转一列
不重复的单点反转，就是每个点只反转一次

使一个矩阵的每一列相等所需要的第 $2$ 种操作数的最小值

在此可以不用考虑反转一行，因为当我们每一列相同时，反转一行一定可以到达 $0$ 矩阵的状态

由于 $n<=20$ 所以我们将一列给状压起来

设 $dp_{i,j}$ 表示使用 $i$ 次不重复的反转可以将某一行状态变为 $j$ 的个数

求出这个 $dp$ 的时间复杂度为 $O(2^n*n^2)$

所以答案为：

a n s = m i n_{i = 0}^{i < 2^{n}} \sum_{j = 0}^{j = n} d p [j] [i] * min (j, n - j)

$ans=min_{i=0}^{i<2^n}\sum\limits_{j=0}^{j=n} dp[j][i]*\min(j,n-j)$

有 $min(j,n-j)$ 的原因是，我们可以将一整列进行反转，所以取反转和不反转的最小值

后记

这个题原本是 $FWT$ 但是本蒟蒻不会 $QWQ$

posted @ 2022-08-19 17:10 轩Demonmaster 阅读(85) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· [HNOI2002]公交车路线

· P3472 [POI2008]MAF-Mafia

· [动态规划] 区间 dp

· 【习题】区间型动态规划

· dp 专题复习

阅读排行：
· 单线程的Redis速度为什么快？
· 展开说说关于C#中ORM框架的用法！
· Pantheons：用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探
· 为什么退出登录或修改密码无法使 token 失效

公告

昵称：轩Demonmaster
园龄： 3年6个月
粉丝： 6
关注： 7

+加关注

2025年3月

日

一

二

三

四

五

六

随笔分类

随笔档案

文章分类

C++(1)

文章档案

2024年10月(1)

OI以痛吻我，我却报之以歌

DP

定理

一个定理（不知道叫啥名）

四边不等式

定义

用途

DilworthDilworthDilworth 定理

状压DP

CF8C Looking for Order

最小斯坦纳树

P6192 【模板】最小斯坦纳树

P3264 [JLOI2015]管道连接

[WC2008]游览计划

分数DP

基本思想

例题

P4377 [USACO18OPEN] Talent Show G

P1642 规划

P2868 [USACO07DEC]Sightseeing Cows G

P4322 [JSOI2016]最佳团体

P3199 [HNOI2009]最小圈

树形DP

P1131 [ZJOI2007] 时态同步

P2016 战略游戏

一般线性DP

P1070 [NOIP2009 普及组] 道路游戏

P1099 [NOIP2007 提高组] 树网的核

前置芝士

将题目翻译成人话

主题思想

P1108 低价购买

解法一：题解O(n2)O(n2)O(n^2)

解法二：个人玄学解法O(nlogn+?)O(nlog⁡n+?)O(n\log n + ?)

解法三：树状数组或者二分求最长下降子序列方案数

P1156 垃圾陷阱

P1169 [ZJOI2007]棋盘制作

P1020 [NOIP1999 普及组] 导弹拦截

CF1562E Rescue Niwen!

题意概述

CF1699D Almost Triple Deletions

状态定义：

结论

区间DP

P5569 [SDOI2008] 石子合并

GarsiaWachs算法

状压DP

CF662C Binary Table

题意简述

问题转化

后记

公告

搜索

常用链接

最新随笔

积分与排名

随笔档案

文章档案

相册

$Dilworth$ 定理

解法一：题解 $O(n^2)$

解法二：个人玄学解法 $O(n\log n + ?)$