整数二分算法（自用）

1.思想

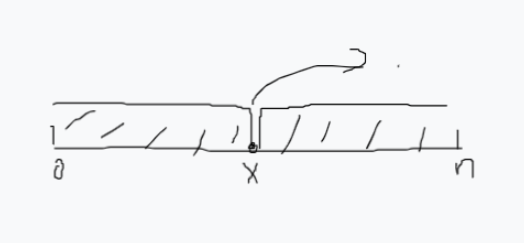
对于一个已排序数组，找到一个点，使得数组被分为两部分，即此点左部和右部（点在左部或右部中的一个），比如数组中小于等于某数x的部分与大于的部分；

对于整数二分而言两个范围之间是没有空隙的，即左部分的边界x的下一个数一定在右部分。我们可以根据题目选择多种方法二分数组，大类上分为两种，寻找大于等于的边界点，寻找小于等于的边界点。具体代码如下。

 

   

2.具体代码

通用模板记住就行！

寻找的边界点属于数组大于等于x的部分

//区间[l,r]被划分成为[l,mid]和[mid+1,r]时：
int bsearch_1(int l,int r)
{
    while (l < r)
    {
	    int mid = l + r >> 1;
	    if (check(mid))r = mid;
	    else l = mid + 1;

    }
    return l;

}

寻找的边界点属于数组小于等于x的部分

//区间[l,r]被划分成为[l,mid-1]和[mid,r]时：
int bsearch_1(int l,int r)
{
    while (l < r)
    {
	    int mid = l + r + 1 >> 1;
	    if (check(mid))l = mid;
	    else r = mid - 1;

    }
    return l;

}

3.应用

题目链接

#include<iostream>

using namespace std;

const int N = 100010;

int n,m;
int q[N];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++)scanf("%d",&q[i]);
    
    while(m--)
    {
        int x;
        scanf("%d",&x);
        
        int l=0,r=n-1;
        while(l<r)
        {
            int mid=l+r>>1;
            if(q[mid]>=x)r=mid;
            else l=mid+1;
            
        }
        if(q[l]!=x)cout<<"-1 -1"<<endl;
        else
        {
            cout<<l<<" ";
            int l=0,r=n-1;
            while(l<r)
            {
                int mid=l+r+1>>1;
                if(q[mid]<=x)l=mid;
                else r=mid-1;
            }
            cout<<l<<endl;
        }
        
    }
    return 0;
}