有依赖的背包问题

题目连接：https://www.acwing.com/problem/content/10/

简单来说就是在子节点和父节点有制约条件下选择物品来取得最大值

 

 其实可以这样想：

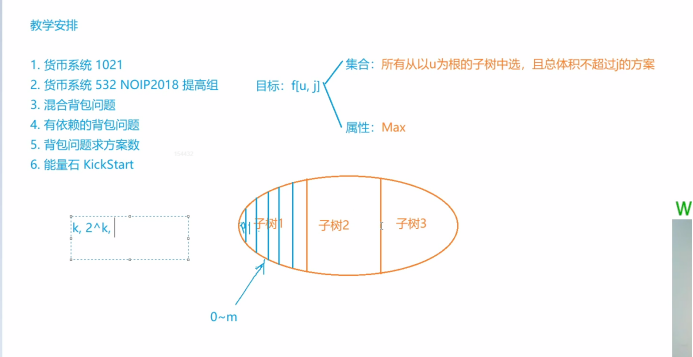
将子树按照体积划分为0~m份，每一份看作一个物品，就可以抽象思维为分组背包，

求f[u,j]的时候一共有三颗子树（上图），每一棵子树内部划分为0~m个情况，分别表示体积是0的时候最大划分价值是多少，体积是1......体积是m的时候最大划分价值是多少，子树内部选择用多大的体积，我们就可以把每个子树看成一个物品组，有m+1个物品,在递归考虑每一课子树的时候，就是一个分组背包问题

为什么要划分体积而不是选择的方案数，因为比如子树有x个，那选择的情况就是2^x，但是x的最大限制是100，2^100是绝对会爆的，所以割的是体积（不得不说y总的思维真的是强)

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int N = 2e2+10;
int n,m;
int w[N],v[N],p;
int dp[N][N];//在以i为根节点的情况下背包容量为j的选择集合
//因为选择方案的决策是很大的，所以割子节点的体积，例如
//求dp[u,j]的时候一共有三颗子树，每一棵子树内部划分为0~m个情况，分别表示体积是0的时候最大划分价值是多少，
//体积是1......体积是m的时候最大划分价值是多少，子树内部选择用多大的体积，
//我们就可以把每个子树看成一个物品组，有m+1个物品。
//在递归考虑每一课子树的时候，就是一个分组背包问题
int root;
int e[N],ne[N],h[N],cnt;
void add(int a,int b)
{
    e[cnt]=b,ne[cnt]=h[a],h[a]=cnt++;
}
void dfs(int u)
{
    for(int i=h[u];~i;i=ne[i])
    {
        int son=e[i];
        dfs(son);
        for(int j=m-w[u];j>=0;j--)//枚举体积需要从大到小因为存了上个子节点的信息
        {
            for(int k=0;k<=j;k++)
            {
                dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[son][k]);
            }
        }
    }
    for(int i=m;i>=w[u];i--)    dp[u][i]=dp[u][i-w[u]]+v[u];//加上根节点的价值
    //在本子树中小于v[i]的是不存在的（因为根节点就有v[i]了所以只能不取这个子树的任何节点）
    for(int i=0;i<w[u];i++)    dp[u][i]=0;
}
int main()
{
    IOS;
    memset(h, -1, sizeof h);//前向星存储最后存入的边初始化记得-1
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i]>>p;
        if(p==-1)   root=i;
        add(p,i);
    }
    dfs(root);
    cout<<dp[root][m]<<endl;
    return 0;
}