cf构造题专练+at小题两道

cf:

1.https://codeforces.com/problemset/problem/1739/B

题目大意：

给定一个数组B，令数组B[i]=abs(a[i]-a[i-1))，你的任务是尽可能的还原A数组，输出任意满足条件的构造数组

做法：

利用题目给出的条件构造数组即可，首先肯定是a[1]=b[1]并且在此之后，根据差分公式可得，a[i]是大于s[i-1]的，并且a[i]还必须是非负数

参考代码

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define int long long
 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
 5 const int N=110;
 6 int t;
 7 int n;
 8 int a[N];
 9 int s[N];
10 void solved()
11 {
12     /*c.clear();
13     cin>>n;
14     int cnt=0;
15     for(int i=0;i<n;i++)
16     {
17         cin>>a[i];
18         if(a[i]!=0)
19         {
20             c.push_back(a[i]);
21         }
22     }
23     b[0]=a[0];
24     if(!is_sorted(c.begin(),c.end()))
25     {
26         cout<<-1<<endl;
27         return ;
28     }
29     for(int i=1;i<n;i++)
30     {
31         b[i]=b[i-1]+a[i];
32     }
33     for(int i=0;i<n;i++)
34     {
35         cout<<b[i]<<" ";
36     }
37     cout<<endl;*/
38     
39     cin >> n;
40     for(int i=1;i<=n;i++)
41     {
42         cin>>a[i];
43     }
44     s[1]=a[1];
45     
46     for(int i=2;i<=n;i++)
47     {
48         if((a[i]<=s[i-1])&&a[i])
49         {
50             cout<<-1<<endl;
51             return ;
52         }
53         s[i]=s[i-1]+a[i];
54     }
55     for(int i = 1; i <= n ; i ++ ) 
56     cout << s[i] << " "; 
57     cout << endl;
58     
59 }
60 signed main()
61 {
62     IOS;
63     cin>>t;
64     while(t--)
65     {
66         solved();
67     }
68     return 0;
69 }

2.https://codeforces.com/problemset/problem/1741/B

大体题意：

要求构造这样的一个数组，满足a[i]!=i的前提下并且与前一位相差1

做法：

现特判，对于n=3肯定是不行的，因为对于1~3肯定有一个数不满足上面的条件，其余的只要是错位输出就满足条件了

可以先输出从3往后的，最后在输出2，1

参考代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int N=2e5+10;
int a[N];
int t;
void solved()
{
    int n;
    cin>>n;
    if(n==3)
    {
        cout<<-1<<endl;
        return ;
    }
    else
    {
        for(int i=3;i<=n;i++)
        {
            cout<<i<<" ";
        }
        cout<<2<<" "<<1<<endl;
    }
}
signed main()
{
    IOS;
    cin>>t;
    while(t--)
    {
        solved();
    }
    return 0;
}

3.https://codeforces.com/problemset/problem/1738/B

大意：

给定一个前缀和数组s，表示的是从s[n-k+1]~s[n]的前缀和数组

前缀和数组定义：

 

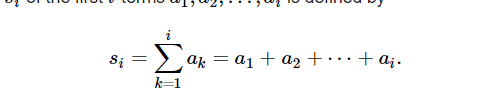
要求判断这个前缀和数组是不是可以被构造的（即满足上面的前缀和定义），并且构成这个前缀和数组的原来a数组还必须是非递减序

做法：

首先k==1，即前n个a[i]的和

另外在根据差分公式还原后k-1个a数组，

并且判断原来的a数组是否是递减的；

假设前n-k+1个a数组的和是b[n-k+2]，那就设前n-k+1个a[i]都等于a[n-k+1]实现最大化

那对于b[n-k+2]来说，肯定是要满足小于等于(n-k+1)*a[n-k+1]的

然后判断是或不是的情况就可以了

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define int long long
 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
 5 const int N=1e5+10;
 6 int a[N];
 7 int n;
 8 int t;
 9 int s[N];
10 int k;
11 void solved()
12 {
13     /*bool flag=false;
14     cnt=0;
15     ans.clear();
16     cin>>n>>k;
17     if(n-k+1<=0)
18     {
19         cout<<"No"<<endl;
20         return ;
21     }
22     for(int i=1;i<=n;i++)
23     {
24         cin>>a[i];
25         ++cnt;
26     }
27     int sum=0;
28     for(int i=n-k+1;i<=n;i++)
29     {
30         sum=0;
31         for(int j=1;j<=i;j++)
32         {
33             sum+=a[j];
34         }
35         ans+=sum;
36     }
37     if(is_sorted(a+1,a+1+n)&&ans==k)
38     {
39         cout<<"Yes"<<endl;
40     }
41     else
42     {
43         cout<<"No"<<endl;
44     }*/
45     cin>>n>>k;
46     for(int i=n-k+1;i<=n;i++)
47     {
48         cin>>s[i];
49     }
50     for(int i=n;i>=n-k+2;i--)
51     {
52         a[i]=s[i]-s[i-1];
53     }
54     if(k==1)
55     {
56         cout<<"Yes"<<endl;
57         return ;
58     }
59     for(int i=n-1;i>=n-k+2;i--)
60     {
61         if(a[i]>a[i+1])
62         {
63             cout<<"No"<<endl;
64             return ;
65         }
66     }
67     int tmp=s[n-k+1];
68     if(tmp<=(n-k+1)*a[n-k+2])
69     {
70         cout<<"Yes"<<endl;
71     }
72     else
73     {
74         cout<<"No"<<endl;
75     }
76 }
77 signed main()
78 {
79    // IOS;
80     cin>>t;
81     while(t--)
82     {
83         solved();
84     }
85     return 0;
86 }

AT回宿舍再写

-------------------------------------------

AT:

1.https://atcoder.jp/contests/abc269/tasks/abc269_c

给定一个数，要求在二进制下从0~n满足这些数的1数位是n的1的子集

举个例子：

 

 AT原例

打印符合这样条件的数字

做法：

枚举n的每一位并且储存1的位置，新建一个vector保存答案。

接下来遍历保存1位置，将答案数组中的每一个数的二进制那一位上的数从0变成1，再将产生的新数保存在答案数组里。

题解参考代码：

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 int main(){
 6   long long x;
 7   cin >> x;
 8   vector<long long> res={0};
 9   for(int d=0;d<60;d++){
10     if(x&(1ll<<d)){
11       int sz=res.size();
12       for(int i=0;i<sz;i++){
13         res.push_back(res[i]|(1ll<<d));
14       }
15     }
16   }
17   sort(res.begin(),res.end());
18   for(auto &nx : res){cout << nx << "\n";}
19   return 0;
20 }

2.https://atcoder.jp/contests/abc269/tasks/abc269_d

大意：蜂巢状图，用来判断连通块的个数

做法：都说了连通块了果断搜索啊，并查集也可以；

参考代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define int long long 
 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
 5 const int N=2e3+10;
 6 const int k=1e3;
 7 int a[N][N];
 8 int n;
 9 int dir[6][2]=
10 {
11     {-1,-1},
12     {-1,0},
13     {0,-1},
14     {0,1},
15     {1,0},
16     {1,1}
17 };
18 bool vis[N][N];
19 int ans;
20 bool check(int cx,int cy)
21 {
22     if(cx<0||cx>=2000||cy<0||cy>=2000)
23     return false;
24     return true;
25 }
26 /*void dfs(int dx,int dy)
27 {
28     /*if(dx>n||dy>n)
29     return ;
30     for(int i=0;i<6;i++)
31     {
32         int nx=dx+dir[i][0];
33         int ny=dy+dir[i][1];
34         if(!a[nx][ny]&&!vis[nx][ny])
35         {
36             vis[nx][ny]=true;
37             dfs(nx,ny);
38             ans++;
39         }
40     }*//*
41     for(int i=0;i<6;i++)
42     {
43         int nx=dx+dir[i][0];
44         int ny=dy+dir[i][1];
45         if(a[nx][ny]&&!vis[nx][ny]&&check(nx,ny))
46         {
47             dfs(nx,ny);
48         }
49     }
50 }*/
51 void dfs(int x, int y) {
52     for(int i = 0; i < 6; i ++ ) {
53         int ix = x + dir[i][0], iy = y + dir[i][1];
54         if(ix < 0 || ix > 2000 || iy < 0 || iy > 2000) continue;
55         if(!a[ix][iy] || vis[ix][iy]) continue;
56         vis[ix][iy] = 1;
57         dfs(ix, iy);
58     }
59 }
60  
61 signed main()
62 {
63     IOS;
64     cin>>n;
65     int s,t;
66     for(int i=0;i<=n;i++)
67     {
68         cin>>s>>t;
69         a[s+k][t+k]=1;
70     }
71     for(int i=0;i<=2000;i++)
72     {
73         for(int j=0;j<=2000;j++)
74         {
75             if(a[i][j]&&!vis[i][j])
76             {
77                 ans++;
78                 vis[i][j]=true;
79                 dfs(i,j);
80             }
81         }
82     }
83     //dfs(0,0);
84     cout<<ans<<endl;
85     return 0;
86 }

 

posted @ 2022-10-27 21:38  江上舟摇  阅读(64)  评论(0)  编辑  收藏  举报