bst算法应用-avl树
avl树,又称平衡二叉树,主要是体现在平衡上,所谓平衡就是左右子树的高度差的绝对值不得超过1,我们也称这个绝对值为blancefactor,bf,平衡因子
关于avl树,它是在bst的基础上建立起来的,但要满足bst又满足平衡的同时,就要思考在插入时如何进行调平;
关于avl树的常考的基本操作是查找,插入和建树,而删除操作很复杂,就不是主流考点了
比较热门的是插入操作,因为这里面涉及到了调平
举个例子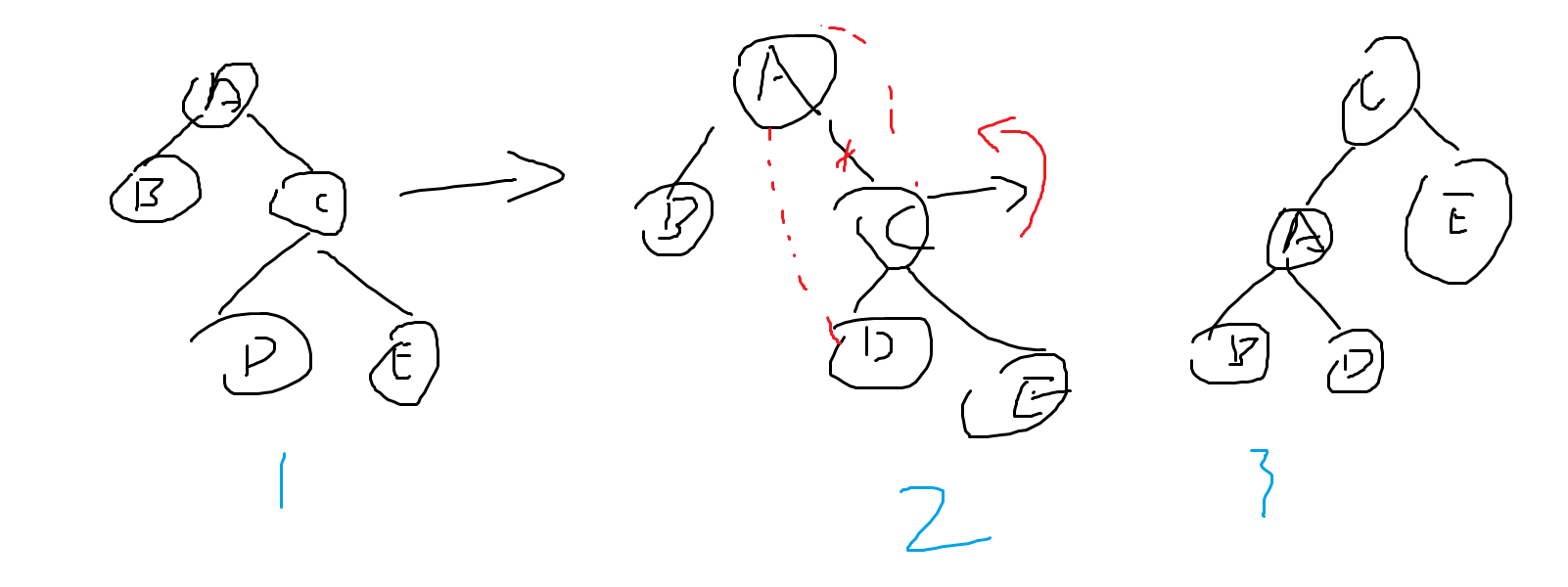
在上图中,如果在插入一个节点在叶节点就会造成失衡,所以说我们要对他做出调整(口误,其实这里是不用进行调平的),显然,上图中c的权值大于a的权值,而e的权值是最大的,b的权值是最小的,所以说就不需要对b与e进行改动
并且上图中满足a<d<c,所以说让d 成为a的右子树,让a成为c的左子树,这个过程由于是以c节点为根进行向左方向进行的调平,我们称其为左旋
而右旋也是同样的
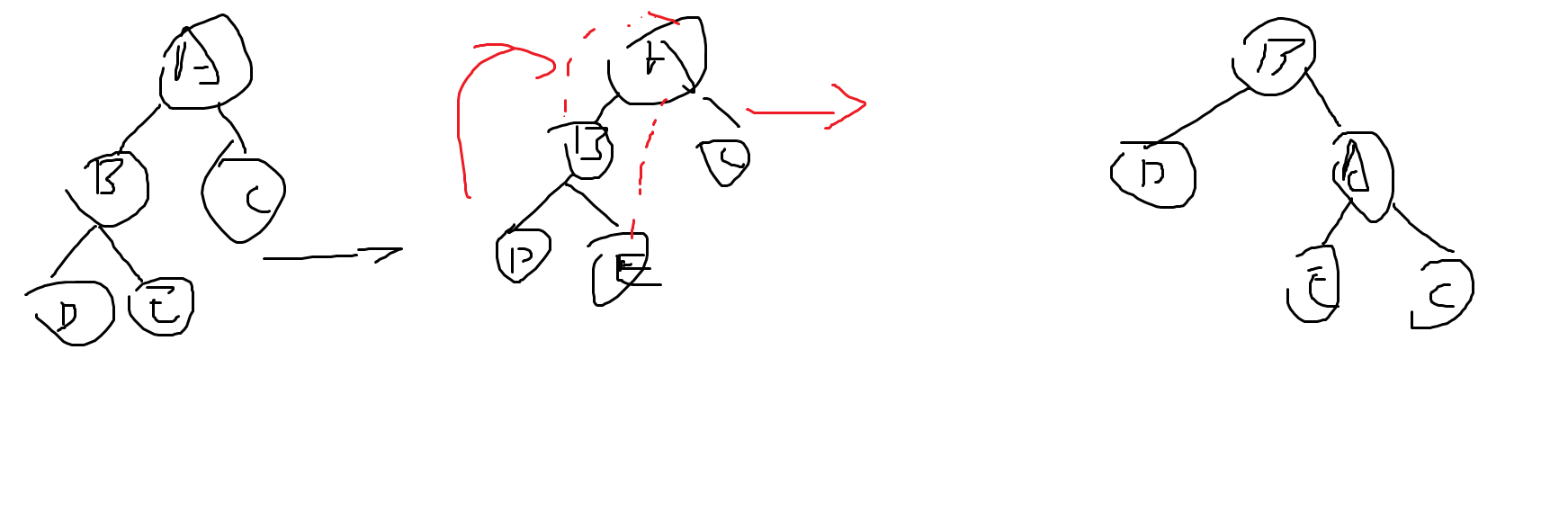
如果我们已经有了一颗确定的avl树,在对他插入一个节点的时候,bf一定会发生变化,根节点的左右子树的高度差就会大于1而失衡,所以说我们要调平的话就要把最靠近插入节点的失衡节点调到正常,路径上的所有节点才会调平
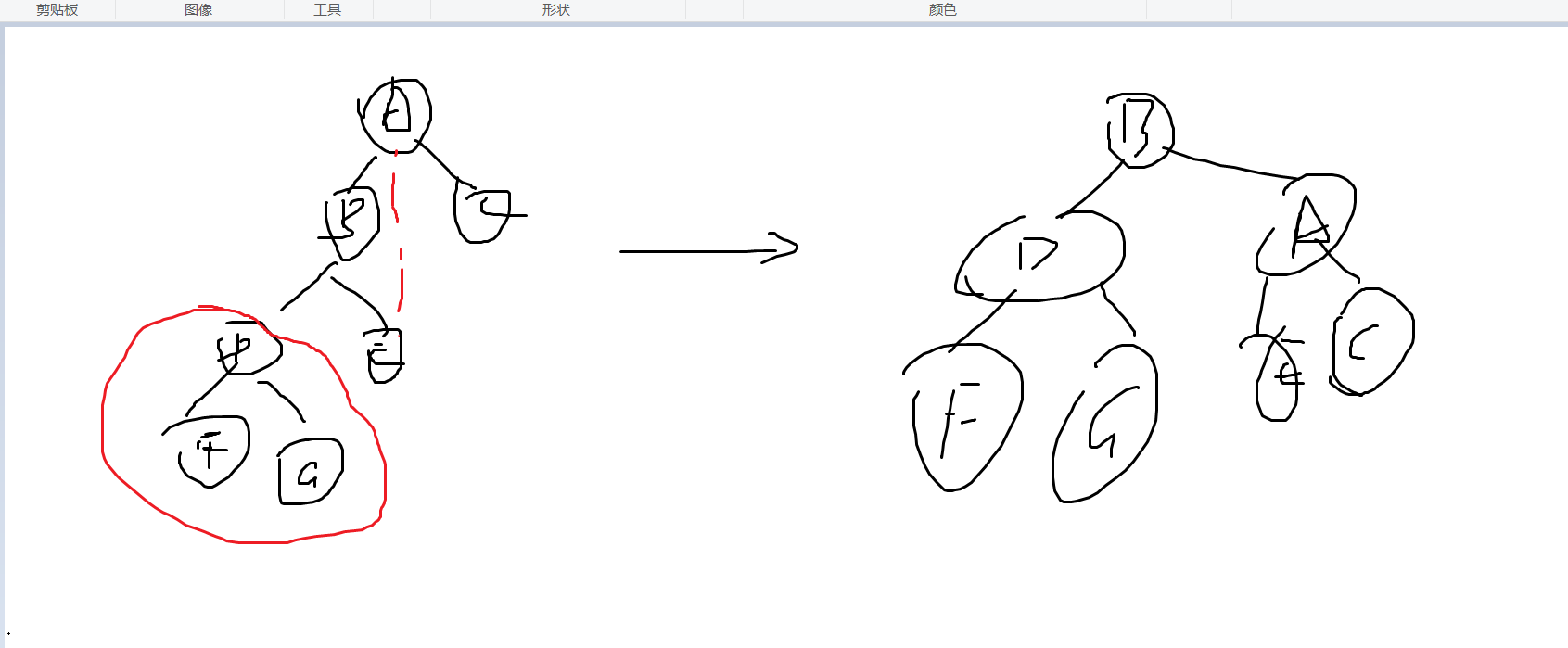
向上图,已经出现失衡情况了,并且我们插入的节点是在不平衡银子节点的左子树的左边,我们称它为LL型
相应,A的bf是2,B的bf是1,当出现2,1,平衡因子时是LL型,那当出现2,-1时是LR型,-2,1与-2,-1是什么型也就清楚了
关于LL型调平,我们将以d节点的左右树包括d节点看成一个节点进行调平即可
RR型也是这样直接进行左旋,
而LR与RL型就有点麻烦了,就需要先进行左旋在进行右旋和先进行右旋在进行左旋了
下面是对于AVL的几种插入情况

题目:pat1066:https://pintia.cn/problem-sets/994805342720868352/problems/994805404939173888
参考代码:
由于用普通的二叉树表示方法出现段错误的情况,只能用二叉树的静态表示法了
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N = 50; 4 struct Node { 5 int data; 6 int height; 7 int l, r; 8 } nodes[N]; 9 int nodeCount = 0; 10 11 int newNode(int data) { 12 nodes[nodeCount].data = data; 13 nodes[nodeCount].height = 1; 14 nodes[nodeCount].l = nodes[nodeCount].r = -1; 15 return nodeCount++; 16 } 17 18 int getHeight(int root) { 19 if (root == -1) { 20 return 0; 21 } else { 22 return nodes[root].height; 23 } 24 } 25 26 void updateHeight(int root) { 27 nodes[root].height = max(getHeight(nodes[root].l), getHeight(nodes[root].r)) + 1; 28 } 29 30 int getBalanceFactor(int root) { 31 return getHeight(nodes[root].l) - getHeight(nodes[root].r); 32 } 33 34 int L(int root) { 35 int temp = nodes[root].r; 36 nodes[root].r = nodes[temp].l; 37 nodes[temp].l = root; 38 updateHeight(root); 39 updateHeight(temp); 40 return temp; 41 } 42 43 int R(int root) { 44 int temp = nodes[root].l; 45 nodes[root].l = nodes[temp].r; 46 nodes[temp].r = root; 47 updateHeight(root); 48 updateHeight(temp); 49 return temp; 50 } 51 52 int insert(int root, int data) { 53 if (root == -1) { 54 return newNode(data); 55 } 56 if (data < nodes[root].data) { 57 nodes[root].l = insert(nodes[root].l, data); 58 updateHeight(root); 59 if (getBalanceFactor(root) == 2) { 60 if (getBalanceFactor(nodes[root].l) == 1) { 61 root = R(root); 62 } else if (getBalanceFactor(nodes[root].l) == -1) { 63 nodes[root].l = L(nodes[root].l); 64 root = R(root); 65 } 66 } 67 } else { 68 nodes[root].r = insert(nodes[root].r, data); 69 updateHeight(root); 70 if (getBalanceFactor(root) == -2) { 71 if (getBalanceFactor(nodes[root].r) == -1) { 72 root = L(root); 73 } else if (getBalanceFactor(nodes[root].r) == 1) { 74 nodes[root].r = R(nodes[root].r); 75 root = L(root); 76 } 77 } 78 } 79 return root; 80 } 81 82 vector<int> pre; 83 84 void preOrder(int root) { 85 if (root == -1) { 86 return; 87 } 88 pre.push_back(nodes[root].data); 89 preOrder(nodes[root].l); 90 preOrder(nodes[root].r); 91 } 92 93 int main() { 94 int n, data, root = -1; 95 scanf("%d", &n); 96 for (int i = 0; i < n; i++) { 97 scanf("%d", &data); 98 root = insert(root, data); 99 } 100 cout<<nodes[root].data; 101 return 0; 102 }
段错误代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define int long long 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0); 5 struct node 6 { 7 int data; 8 int height; 9 node *l; 10 node *r; 11 node (int data=0,int height=1,node *l=NULL,node *r=NULL):data(data),height(height),l(l),r(r){} 12 }; 13 int n; 14 int a[30]; 15 int v; 16 int getheight(node *&root) 17 { 18 if(root==NULL) 19 return 0; 20 return root->height; 21 } 22 void updataheight(node *&root) 23 { 24 root->height=max(getheight(root->l),getheight(root->r))+1; 25 } 26 int getblancefactor(node *&root) 27 { 28 return (getheight(root->l)-getheight(root->r)); 29 } 30 void lrevolve(node *&root) 31 { 32 node *tmp=root->r; 33 root->r=tmp->l; 34 tmp->l=root; 35 updataheight(root); 36 updataheight(tmp); 37 root=tmp; 38 } 39 void rrevolve(node *&root) 40 { 41 node *tmp=root->l; 42 root->l=tmp->r; 43 tmp->r=root; 44 updataheight(root); 45 updataheight(tmp); 46 root=tmp; 47 } 48 void insert(node *&root,int x) 49 { 50 if(root==NULL) 51 { 52 root=new node; 53 root->data=x; 54 root->height=1; 55 root->l=root->r=NULL; 56 return ; 57 } 58 if(root->data>x) 59 { 60 insert(root->l,x); 61 updataheight(root); 62 if(getblancefactor(root)==2) 63 { 64 if(getblancefactor(root->l)==1) 65 { 66 rrevolve(root); 67 } 68 else if(getblancefactor(root->l)==-1) 69 { 70 lrevolve(root->l); 71 rrevolve(root); 72 } 73 } 74 } 75 else 76 { 77 insert(root->r,x); 78 updataheight(root); 79 if(getblancefactor(root)==-2) 80 { 81 if(getblancefactor(root->r)==-1) 82 { 83 lrevolve(root); 84 } 85 else if(getblancefactor(root->r)==1) 86 { 87 rrevolve(root->r); 88 lrevolve(root); 89 } 90 } 91 } 92 } 93 /*node *buildtree(node *&root) 94 { 95 for(int i=0;i<n;i++) 96 { 97 cin>>v; 98 insert(root,v); 99 } 100 return root; 101 }*/ 102 signed main() 103 { 104 IOS; 105 node *root; 106 cin>>n; 107 //for(int i=0;i<n;i++) 108 // { 109 //cin>>a[i]; 110 //} 111 // root=buildtree(root); 112 for(int i=0;i<n;i++) 113 { 114 cin>>v; 115 insert(root,v); 116 } 117 cout<<root->data; 118 return 0; 119 }
本文来自博客园,作者:江上舟摇,转载请注明原文链接:https://www.cnblogs.com/LQS-blog/p/16595536.html



