AtCoder Beginner Contest 263(A~D) ect
好久没写博客了，今天正好刚打完比赛更一下
贪心题目我已经刷了将近30道了，由于那几天考驾照就没写，以后有空的时候补过来吧，都在codeblock里
pat的题也刷了点，acwing 的题也刷了点，基本都攒下了。以后也会慢慢补过来的
这几天都在备战四级，上午司机下午算法，有点忙不过来就一直没写博客，今天打完比赛就想趁热写一下吧，正好昨天也做了22年夏的甲级考试
先说一下爱扣的比赛：
A题：https://atcoder.jp/contests/abc263/tasks/abc263_a
题目大意：给定五个数，要求判断这样的条件：
如果有三个数相同并且其余两个数是其他相等的数
满足就y不满足就n了
题目思路：这道题可能我做的有点麻烦了，我是在输入5个数后分别插入set里，然后在以set为准检验这五个数，当然，只检验1遍，
拿样例来说的话是以1为标准，检验1，2，1，2，1；
如果set内只有两个数并且计数器为2，3的话就是y了反之n
参考代码：
#include<bits/stdc++.h>// atcoder a using namespace std; #define int long long #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0); int s[10]; set<int>q; int cnt; signed main() { IOS; bool flag=false; for(int i=0;i<5;i++) { cin>>s[i]; q.insert(s[i]); } set<int>::iterator it; for(it=q.begin();it!=q.end();it++) { for(int i=0;i<5;i++) { if(*it==s[i]) { // s.erase(s.begin()+i); cnt++; } } break; } if(q.size()==2&&(cnt==2||cnt==3)) cout<<"Yes"<<endl; else cout<<"No"<<endl; return 0; }
估计这么麻烦来做一个签到提的话恐怕就只有我这种傻叉了吧.......
题目评价：易，别人都用暴力枚举了........
B题:https://atcoder.jp/contests/abc263/tasks/abc263_b
题目大意：找father问题
给定n个人，第i（2<=i<=n)个人是第p[p[i]]个人的父亲（是不是有点绕口）并且满足pi<i，求有多少代？
题目思路：面向样例分析，
给定的
n:3
pi:1,2;
i : 2,3;
这样分析：p[2]是p[p[2]]的父亲==p[2] is p[1]'s father
同理 p[3]是p[p[3]]的父亲也就是p[3] 是 p[2]的父亲
然后就可以dfs啦
其实我好像又做麻烦了，我做完发现这道题数据好像水的很，甚至用一个递推式a[i]=a[p[i]]+1都能实现
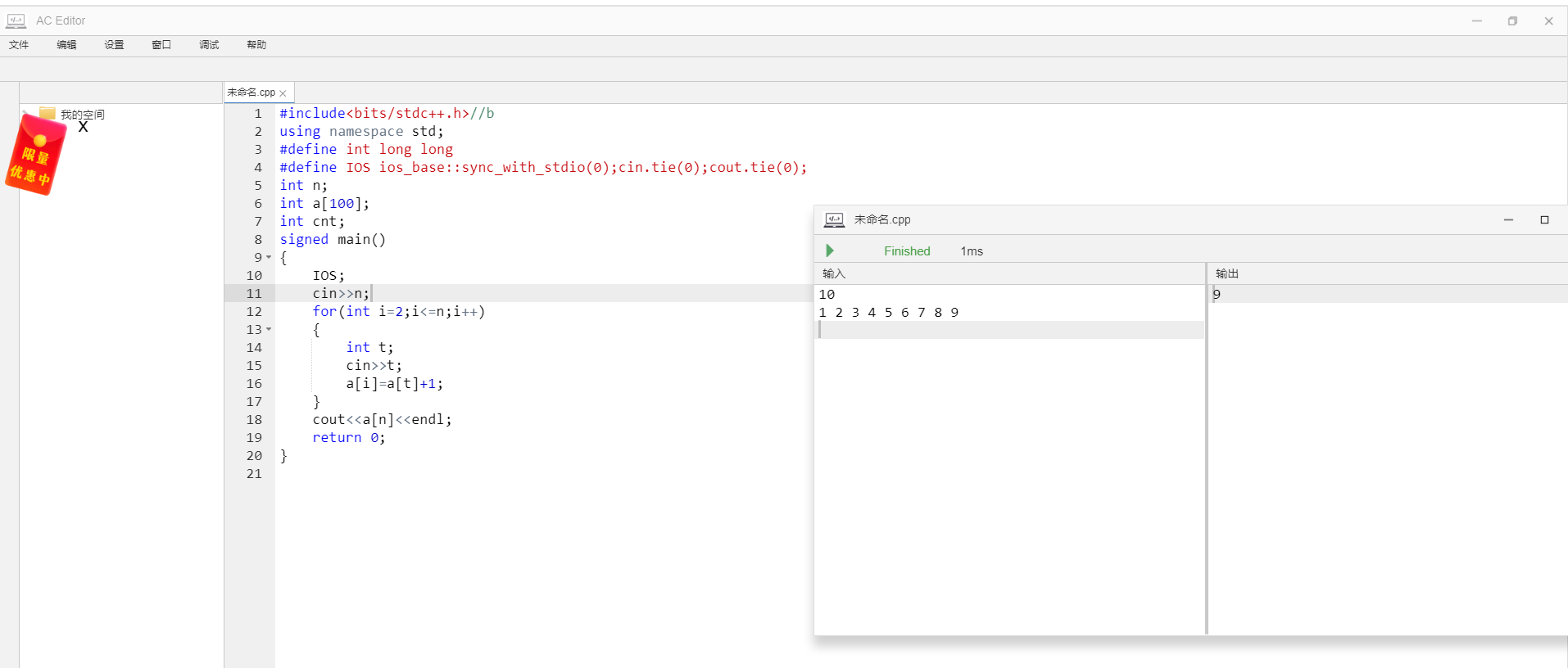
好吧，dfs可以过不水的题（又作麻烦了）
参考代码：
1 #include<bits/stdc++.h>//b 2 using namespace std; 3 #define int long long 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0); 5 int n; 6 int p[100]; 7 int cnt; 8 void dfs(int r) 9 { 10 if(r==1) 11 return ; 12 cnt++; 13 dfs(p[r]); 14 } 15 signed main() 16 { 17 IOS; 18 cin>>n; 19 for(int i=2;i<=n;i++) 20 cin>>p[i]; 21 dfs(n); 22 cout<<cnt; 23 return 0; 24 }
C题：https://atcoder.jp/contests/abc263/tasks/abc263_c
题目大意：不会吧不会吧都2202年了还有人出纯排列组合？
这不送分吗？？？
题目分析：以前我排列组合好像发过题解哎：https://www.cnblogs.com/LQS-blog/p/15862393.html
参考代码：
惨不惨考吧，算了还是写上吧：
1 #include<bits/stdc++.h>//c 2 using namespace std; 3 #define int long long 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0); 5 int n,m; 6 int a[20]; 7 signed main() 8 { 9 IOS; 10 cin>>n>>m; 11 for(int i=n+1;i<=m;i++) 12 a[i]=1; 13 do{ 14 for(int i=1;i<=m;i++) 15 { 16 if(!a[i]) 17 cout<<i<<" "; 18 } 19 cout<<endl; 20 }while(next_permutation(a+1,a+1+m)); 21 22 return 0; 23 }
D题：https://atcoder.jp/contests/abc263/tasks/abc263_d
题目大意：给定一个长度为n的数组，并且给定两个选择：
x选择：如果x是0，就不变，如果是>=1,就把a1~an全部用L替换
y选择，前半部分同上，后半部分是如果>=1,就把an,an-1..........an-y+1换成R；
题目的要求是经过x和y选择这组数组最小和是多少
题目思路：我起手本来想累加两个sum1，sum2来和总sum比大小然后在置换数组；
但读了一遍之后发现自己想简单了
经典分析样例：
我再次分析的是
5 4 3
5 5 0 6 3
从a[1]开始一直找到a[i]<L到0，然后将前面的替换成L，再把后面R；
当然这样分析第二组样例就直接适用了不用换
第三组样例就不行了
要是按照上面分析的话总和会是-44；
但是要是得到-58的话必须是上面中靠下的数组即：
-5，-5，-5，-5，-5，-5，-5，-5，-15，-3
但是这样的话是怎么得来的呢？
这样算的话，就要考虑部分和与总和之间的关系了，就是前i段区间的和与连续L的和孰大孰小的问题了，如果是某段区间和更小的话，当然，这前i段的区间和就可以取a[1]+..a[i]或者是i*L了；
那再来考虑剩下y的问题，其实也是差不多的思想了：
确定了前i区间和了就可以直接从后往前推，因为前i区间的和被确定了之后它的后一段区间的和也会被确定，我们只需要从后往前确定sum总和与区间和变换之后的就是a[n]+...a[i]+R*(n-i)（因为y的操作是酱紫的）
那就可以来写了，当然，我起手是想用前缀和，因为这道题和我前段时间一个训练赛中的题目有点相似，那个题是因为题目数据太大了所以用前缀和来处理，这里我本来想用奈何本人的代码实现能力实在是堪忧，所以说就改用了求前n段区间内最小的dp思想，其实这类题也是在蓝桥杯的真题中出现了不少了，我还发过题解：https://www.cnblogs.com/LQS-blog/p/15986825.html；；；
https://www.cnblogs.com/LQS-blog/p/15986873.html
思想类似；
参考代码：
1 #include<bits/stdc++.h>//d 2 using namespace std; 3 #define int long long 4 #define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0); 5 const int N=2e5+10; 6 int n; 7 int L; 8 int R; 9 int a[N]; 10 int dp[N]; 11 int sum=1e18; 12 signed main() 13 { 14 IOS; 15 cin>>n>>L>>R; 16 for(int i=1; i<=n; i++) 17 { 18 cin>>a[i]; 19 dp[i] = min(dp[i-1] + a[i], i * L); 20 //sum += a[i]; 21 } 22 for(int i=n; i>=0; i--) 23 sum = min(sum, dp[i] + R * (n - i)); 24 cout << sum << endl; 25 return 0; 26 }
后面的E,F,G,EX没做出来，明天或者后天补题
本文来自博客园，作者：江上舟摇，转载请注明原文链接：https://www.cnblogs.com/LQS-blog/p/16558256.html
