归并排序的经典-求逆序对

本来今天poj崩掉了，并且求逆序对也是个很简单的问题，罗黑上的分治的题也都刷完了（其实难得一见上罗黑的练习题上的简单题目），东哥的题又刷不动，打算今天就到这了

但是一想到以前也没有总结过逆序对的求法，写完这个总结在做一道每日一题就休息了；

先认识一下什么是逆序对，举一个例子：

 

上述写的够清楚了吧（电脑写字很烂，见谅）

归并排序我相信不用多介绍了吧？都相信已经学了，算了，要不概括一下归并排序的核心吧：

归并排序的核心其实就是先将每个元素初始化为子集，两两子集合并，实现内部排序，一直这样处理知道最后剩下一个集合

稍微说一下合并：

要归并两个有序的子序列

例如我们要归并a[]={13,94,99},{34，56}这两个子序列

 

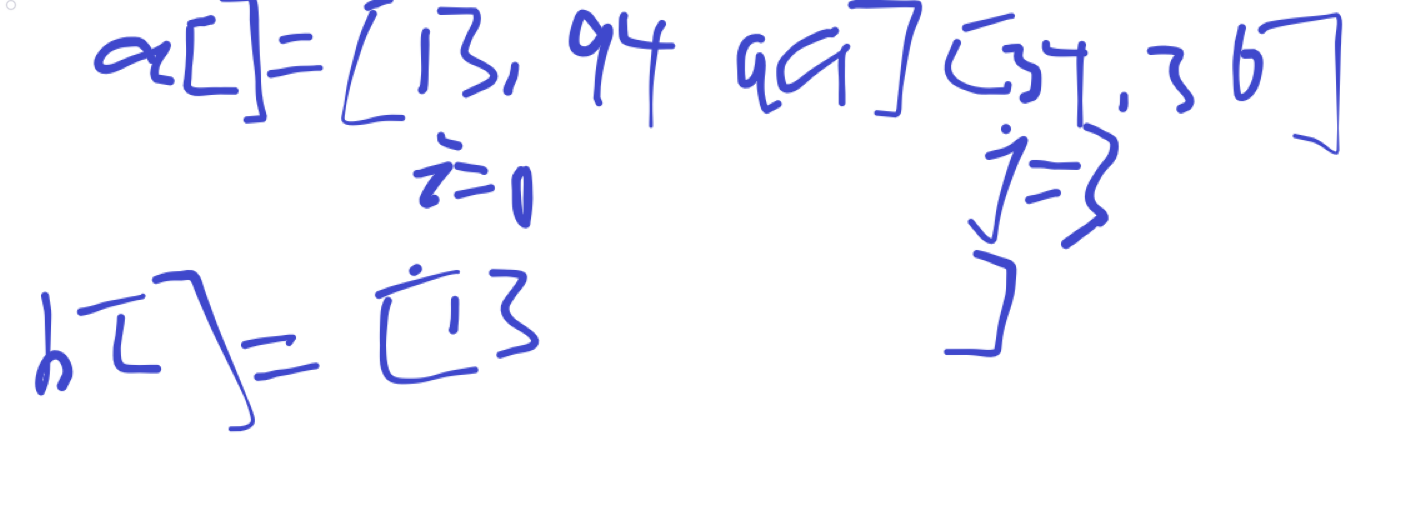
 将i,j分别指向子序列的第一个数，进行一次比较发现a[i]<a[j]，则将a[i]放在辅助数组b中，经过四次比较

最终可得b[]={13,34,56,94,99}

第二次比较

 

 第三次比较

 

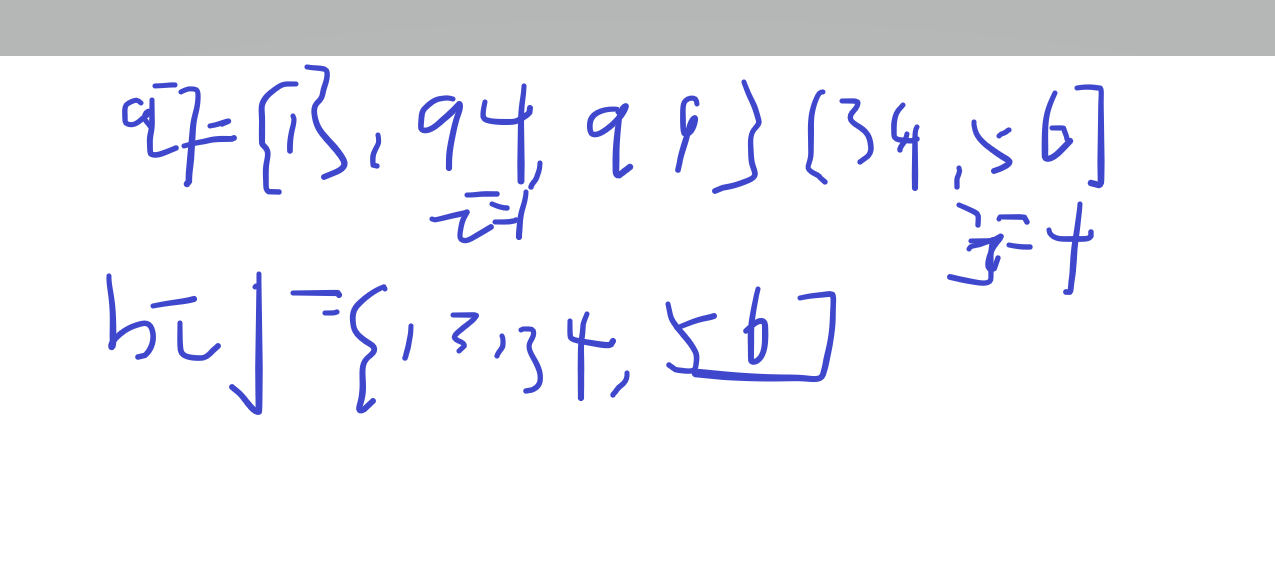
 第四次比较

 

 具体来看题目：

http://acm.hdu.edu.cn/showproblem.php?pid=4911

题目大意：

给定一个数组，交换相邻任意两个元素，且不超过k次，求最少的逆序对有多少？

题目分析：当k=0的时候即求原始数组中有多少对逆序对，并且在每次合并中，如果子序列内部是有序的则不存在逆序对；

在合并两个子序列时，若前子序列的元素大于后子序列的元素则产生逆序对，像上面四次合并，并且在每次合并的时候，可能出现不止一对逆序对，

例如在第二次合并的时候，就出现了{34，96}，{34，99}两对逆序对

那分别讨论原始数组中的逆序对cnt，若cnt<=k则说明不够交换k次，即最少逆序对为0对

若cnt>k则说明k次交换都发生在逆序的相邻元素上，则有最少cnt-k对

解题思路：分治法，归并排序

难度评价：易

参考代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int N=1e5+10;
int a[N];
int b[N];
int cnt;
int n,k;
void Merge(int L,int mid,int R)
{
    //归并
    int i=L;
    int j=mid+1;
    int t=0;
    while(i<=mid&&j<=R)
    {
        if(a[i]>a[j])
        {
            b[t++]=a[j++];
            cnt+=mid-i+1;//出现逆序对
        }
        else
            b[t++]=a[i++];
    }
    //检查
    //一个子序列中的数都处理完了，另一个还没有，把剩下的复制过来
    while(i<=mid)
        b[t++]=a[i++];
        while(j<=R)
            b[t++]=a[j++];
        //数组拷贝
        for(int i=0;i<t;i++)
            a[L+i]=b[i];
}
void mergesort(int low,int high)
{
    if(low<high)
    {
        int mid=(low+high)/2;
        //分
        mergesort(low,mid);
        mergesort(mid+1,high);
        //治
        Merge(low,mid,high);
    }
}
signed main()
{
    IOS;
    while(cin>>n>>k)
    {
        cnt=0;
        for(int i=0;i<n;i++)
        {
            cin>>a[i];
        }
        mergesort(0,n-1);
        if(cnt<=k)
            cout<<0<<endl;
        else
            cout<<cnt-k<<endl;
    }
}