小知识点普及：裴蜀等式

在数论中，裴蜀等式（英语：Bézout’s identity）或贝祖定理（Bézout’s lemma）是一个关于最大公约数（或最大公约式）的定理。裴蜀定理得名于法国数学家艾蒂安·裴蜀，说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：
ax + by = m 有整数解时当且仅当m是d的倍数。
裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用扩展欧几里得算法(Extended Euclidean algorithm)求得。

例如，12和42的最大公因数是6，则方程12x+42y=6有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。

特别来说，方程 ax+by=1 有整数解当且仅当整数a和b互素。
裴蜀等式也可以用来给最大公约数定义： d其实就是最小的可以写成ax+by形式的正整数。(这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。)

证明:

如果

和 中有一个是 0，比如 ，那么它们两个的最大公约数是 。这时裴蜀等式变成 ，它有整数解 (x,y) 当且仅当 是 的倍数，而且有解时必然有无穷多个解，因为 可以是任何整数。定理成立。
以下设 a和 b 都不为0。
设 ，下面证明A中的最小正元素是 a 与 b 的最大公约数。
首先， 不是空集（至少包含 和 ），因此由于自然数集合是良序的， 中存在 最小正元素 。考虑 中任意一个 正元素 对 的带余除法：设 ，其中 为正整数， 。但是

而 已经是集合 中最小的正元素了，又 ,所以 。
因此 。也就是说，A中任意一个正元素p都是 的倍数，特别地： 。因此 是 和 的公约数。
另一方面，对 a 和 b 的任意正公约数 ，设 ，那么

,因此 。所以 是 和 的最大公约数。
在方程 中，如果 ，那么方程显然有无穷多个解：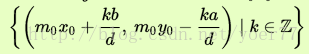

相反的，如果 有整数解，那么 ，于是由前可知 （即 ）。
m=1时，方程有解当且仅当a、b互质。方程有解时，解的集合是

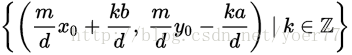
其中 是方程ax+by=d的一个解，可由辗转相除法得到。
所有解中，有且仅有一个解(x,y) 满足
。

为扩展欧几里得做铺垫的裴蜀等式