杭电Fibonacci Numbers（难度极高，但是经典的矩阵快速幂问题的求解）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3117；

温馨提示：这道题有一定的数学难度和代码难度，不是非要搞懂这道题和彻底贯彻矩阵快速幂的应用劝退，不要和一个难题死磕；

题目思路：

这个题是很经典的，求解10^9个斐波那契数列；

但是这样肯定会溢出栈，10^9用long long 都显得有点苍白了更别说第10^9个斐波那契数列；

要知道，斐波那契数列的增长速度是极快的，用递推式根本无法完成；

所以说这个题将斐波那契数列转化成矩阵存储，然后计算矩阵的10^9幂；

这个题的思路可以转化成几个函数一起求解；

当然，矩阵快速幂我们已经了解过了：矩阵乘法+快速幂运算的结合体，

那这个题就是矩阵快速幂+斐波那契数列打表+数学转化+转制问题+......很多复杂的运算，所以说，这道题以向我这样的初级阶段acmer，理解思想和初步实现代码就ok了；

总之，这个题有难度，没事的时候可以当一个思维和数学的题来啃一啃，当然，还是离不开矩阵快速幂的运算：

Talk is cheap. Show me the code.

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100;
ll F[N];
const int M = 2;
const int MOD = 10000;
struct Matrix{
    ll m[M][M];
    Matrix(){
        memset(m, 0, sizeof(m));
    }
};
void solve(){
    F[1] = F[2] = 1;
    for(int i = 3; i < N; i++){
        F[i] = F[i - 1] + F[i - 2];
    }
}
// 矩阵乘法
Matrix mul (const Matrix& a , const Matrix& b){
    Matrix ans;
    for (int i = 0; i < M; ++i){
        for(int j = 0; j < M; ++j){
            for (int k = 0; k < M; ++k){
                ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;
            }
        }
    }
    return ans;
}

// 矩阵快速幂取模
Matrix fast_exp_mod(Matrix a, int n){
    Matrix ans;
    for(int i = 0; i < M; i++){
        ans.m[i][i] = 1;
    }
    while( n > 0){
        if( n & 1 ){
            ans = mul(ans,a);
        }
         a = mul( a, a );
        n >>= 1;
    }
    return ans;
}

const double s = 1.0*(1 + sqrt(5.0))/2;

void deal(int n){
    Matrix base;
    base.m[0][0] = 1;
    Matrix a;
    a.m[0][0] = a.m[0][1] = a.m[1][0] = 1;
    Matrix ans = fast_exp_mod(a, n-1);
    ans = mul(base, ans);
    double b = -0.5 * (log(5) / log(10)) + n*log(s) / log(10);
    b -= floor(b);//取地板函数
    double x = pow(10.0, b);
    while( x < 1000){
        x *= 10;
    }
    printf("%lld...%04lld\n", (ll)x, ans.m[0][0]);
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();//打表处理斐波那契数列
    int n= 0;
    while(~scanf("%d", &n)){
        if( n < 40){
            printf("%lld\n", F[n]);//小于第40个的斐波那契直接输出即可，能容下
        }else{
            deal(n);//其余情况另作处理
        }
    }
    return 0;
}

 补充：与这道题相辅相成的是这道题http://poj.org/problem?id=3070

这道题中解释了普通一维递推式转置二维运算矩阵的大略；

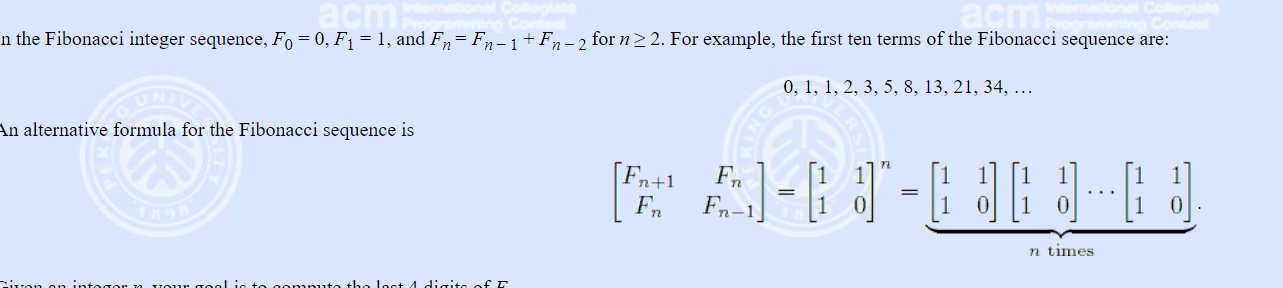
 还有一道也是递推转置的题：

http://acm.hdu.edu.cn/showproblem.php?pid=6030

留着明天做吧