洛谷最大长方形

题目链接：https://www.luogu.com.cn/problem/P1387

有趣的dp思维题，可以一试；

题目思路：

dp三步走，设状态，转移方程，dp结果

设dp[i][j]为以i，j为左下点的正方形的最长边长；

第二步转移方程：

dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;

为什么要这样写，请看图片

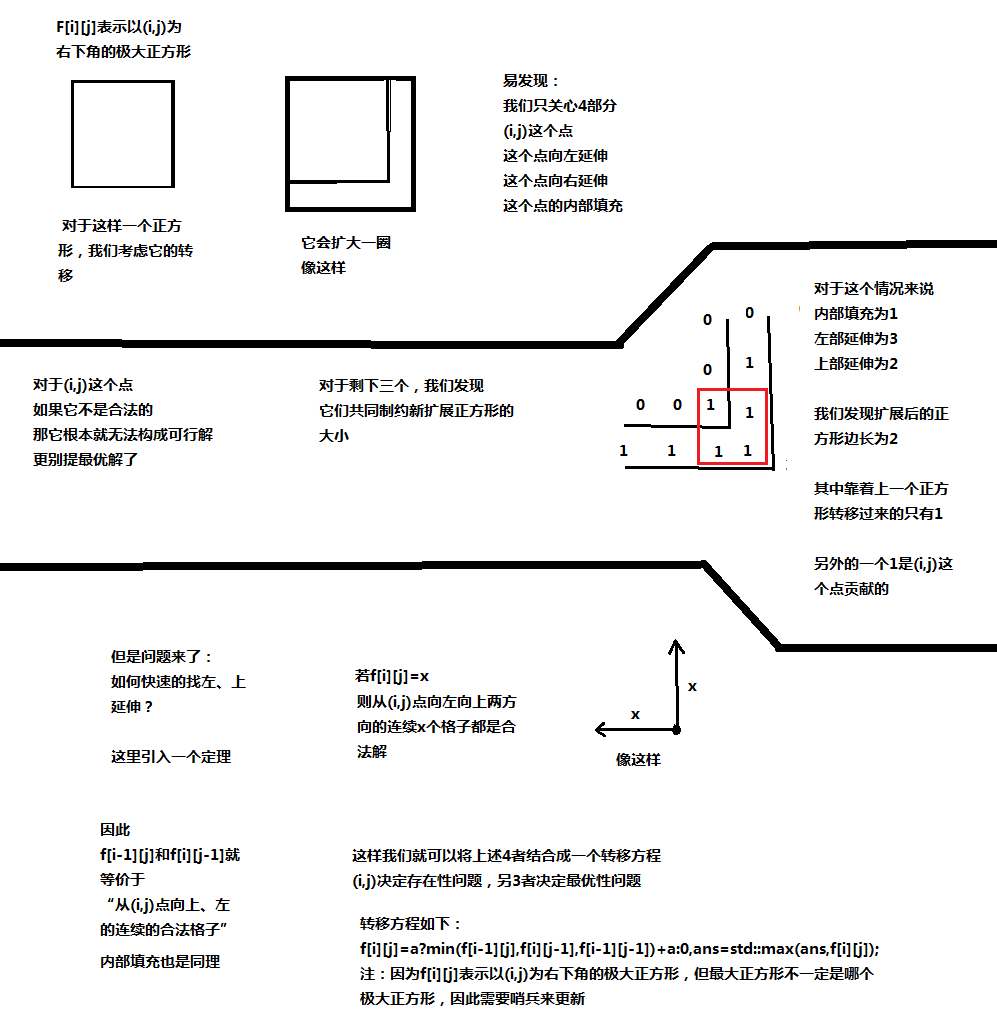
图片转自大佬：https://www.luogu.com.cn/blog/Panthera/solution-p1387

然后边界条件的处理和一些转移的运算都在代码中啦：

#include<bits/stdc++.h>
using namespace std;
int dp[110][110];
int a[110][110];
int n,m;
int ans;
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(register int i=1;i<=n;i++)
    {
        for(register int j=1;j<=m;j++)
        {
            cin>>a[i][j];
        }
    }
    for(register int i=1;i<=n;i++)
    {
        for(register int j=1;j<=m;j++)
        {
            if(a[i][j]==1)//只有是1才可以处理哦 
            {
                dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;//已经说过了，其实无非就是左，下和左下三个重要方向以及i,j本身一个点所贡献的边长 
                ans=max(ans,dp[i][j]);//每次求最大的边长 
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}