关于矩阵运算的相关总结以及oj训练题矩阵的幂次运算

首先来认识一下矩阵乘法，矩阵乘法就是两个矩阵相乘，当然，要相乘的话还要满足一定条件——第一个矩阵的列数等于第二个矩阵的行数

具体来演示一下矩阵运算的规则：

矩阵的运算如上所示，更具体的需要去学离散数学，（大一狗表示没学呜呜），然后对于就两个矩阵相乘，代码如下：

for(int i=0;i<n;i++)   //矩阵c是a与b相乘得到的 
      for(int j=0;j<p;j++) //n*p（n行p列） 
        for(int k=0;k<m;k++)
          c[i][j]+=a[i][k]*b[k][j];

 

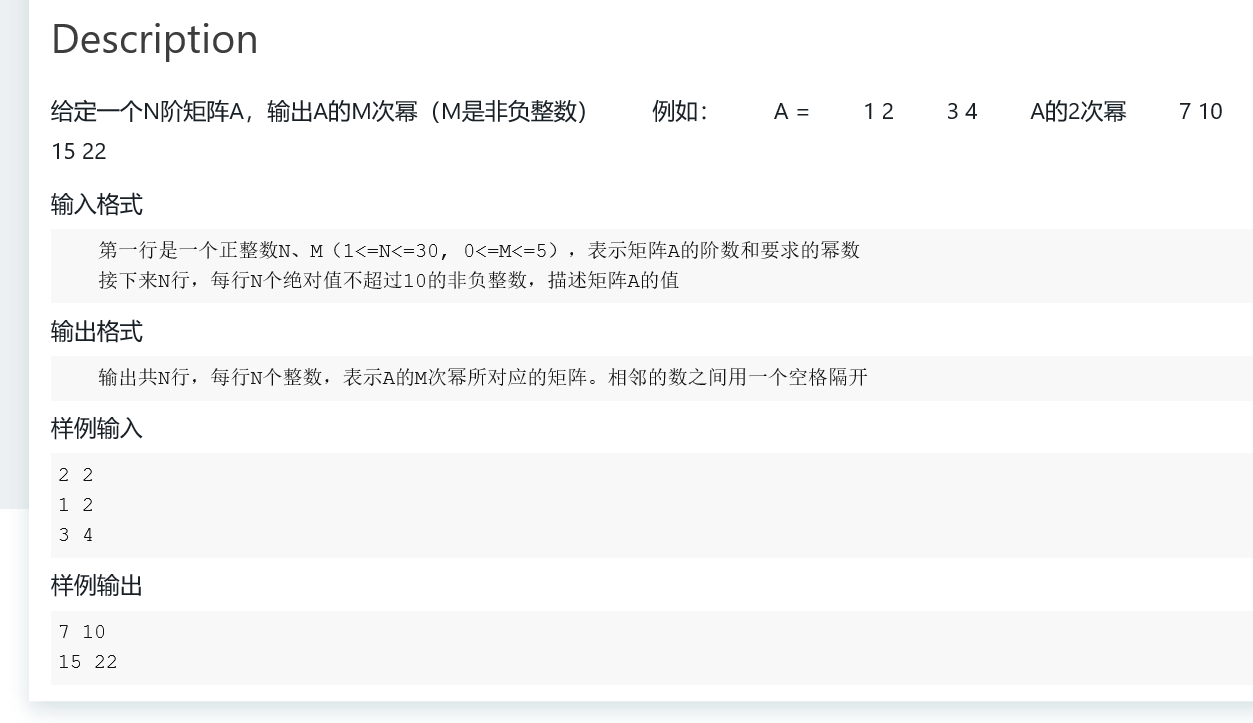
 注意事项以及ac代码如下：

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
int a[50][50];//原始输入 
int b[50][50];//备份，并且最后用来输出 
int c[50][50];//运算结果 
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            cin>>a[i][j];
            b[i][j]=a[i][j];//用来备份 
        }
    }
    if(m==0)
    {
        memset(b,0,sizeof(b));
        for(int i=0;i<n;i++)
            b[i][i]=1;//单位矩阵，如同数的乘法中的1,相当于初始化 
    }
    else 
    {
        for(int p=0;p<m-1;p++)//m次方 
        {
            for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                for(int k=0;k<n;k++)
                {
                    c[i][j]+=a[i][k]*b[k][j];//模拟运算 
                }
            }
        }
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            {
                b[i][j]=c[i][j];//反过来赋值，用于下一次相乘 
                c[i][j]=0;//回溯 
            }
        }
    }
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            cout<<b[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

当然，这一种是麻烦做法，

优化做法是快速幂矩阵运算，

可是，我不会( •̀ ω •́ )y

------------------------------------------------（手动分割线）

2022-4-16更

嗨嗨嗨，来了啊，时隔一个多月的我有来了，这次我学会了矩阵快速幂

对于上述求矩阵运算的要求和规则还是不变的

原理还是：给定一个m*m的矩阵，求他的矩阵^m，依靠快速幂的话，就是将矩阵看作底数进行运算就可以了

那？怎么办呢？还是要依靠矩阵乘法的原则的，在矩阵乘法的基础上，展开对于快速幂的运算

Talk is cheap. Show me the code

#include<bits/stdc++.h>
using namespace std;
struct matrix
{
    int m[40][40];
    matrix()//初始化矩阵
    {
        memset(m,0,sizeof(m));
    }
};
matrix multi(matrix a,matrix b)//矩阵乘法
{
    matrix res;
    for(register int i=0;i<30;i++)
        {
            for(register int j=0;j<30;j++)
            {
                for(register int k=0;k<30;k++)
                {
                    res.m[i][j]+=a.m[i][k]*b.m[k][j]; 
                }
            }
        }
        return res;
}
int n,m;
matrix fastm(matrix a,int m)//以二进制为依托的快速幂算法
{
    matrix res;
    for(register int i=0;i<30;i++)
    res.m[i][i]=1;//初始化矩阵，相当于让底数为1，就是前面快速幂讲的res=1
    while(m)
    {
        if(m&1)
        res=multi(res,a);
        a=multi(a,a);
        m>>=1; 
    }
    return res;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin>>n>>m;
    matrix a;
    for(register int i=0;i<n;i++)
    {
        for(register int j=0;j<n;j++)
        {
            cin>>a.m[i][j];
        }
    }
    matrix ans=fastm(a,m);
    for(register int i=0;i<n;i++)
    {
        for(register int j=0;j<n;j++)
        {
            cout<<ans.m[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}