高精度四件套（加减乘除）

唉，和高精度打交道真不是一件简单事，尤其是高高除，但是在经过参考各位大佬，巨佬，大神，神仙，大牛，大犇资料的时候，我发现自己对于他们的思路以及代码清晰度的辨识还不是很高，所以下定决心写一篇高精度的专题，以便自己日后用来复习高精度，并且根据我的思路写出我的高精度代码；

首先我们先来认识一下，为什么要用高精度：简单而言，对于一些非常大的数字，用普通的long甚至是longlong都已经处理不了了，比如处理10^1000，这个数肯定不能用普通变量来存储了，我们这时候就需要手写高精度运算

基本整数类型的取值范围

类型	数值范围	占字节数
char	-128 .. 127	1
unsigned char	0 .. 255	1
int (long)	-2147483648 .. 2147483647	4
unsigned int (long)	0 .. 4294967295	4
long long	-9223372036854775808 .. 9223372036854775807	8
unsigned long long	0 .. 18446744073709551615	8

如何存储高精度数字呢，我们通常采取以输入字符或者是字符数组之后通过整形数组来存储高精度数字。

 

一、高精度加法

洛谷题目链接：https://www.luogu.com.cn/problem/P1601

拿到题我们其实很稀奇的，咦，测试样例这么这么简单吗？直接写printf("%d",a+b);不就行了吗？哈哈哈，这就是“稻花香里说丰年”——听取WA声一片。要关注一下数据的取值范围a,b≤10^500,这是个什么概念？去百度搜索一下10的100次方就知道了。

那么该怎么才能AC呢？这时候就要用高精度了，首先我们先定义合适的数据范围，比如它给的是10^500，我们就可以定义两个数量为510（当然更大也没关系）的char数组，用来输入数字用，在定义两个int类型的数组，用来存储数据。

然后在模拟一下加法运算，是的，高精度运算也是一种模拟运算，比如：

模拟完成之后，我们得到的结果或许带着前导0，所谓前导0就是0123，我们需要输出123，这个0通过条件判断删去就可以了。

总结：

1、定义存储数组。

2、读入数据到数组中。注意是倒序存放，也就是个位放在数组下标为 0 的地方。

3、从个位开始模拟竖式加法的过程，完成整个加法。

4、删除前导0。

5、输出加法的结果。

代码如下：

#include<bits/stdc++.h>
using namespace std;
char a[510],b[510];//用来输入大数 
int c[510],d[510];//用来存储数据 
int main()
{
    scanf("%s %s",a,b);
    int len1=strlen(a);
    int len2=strlen(b);
    for(int i=0;i<len1;i++)
    {
        c[i]=a[len1-1-i]-'0';//逆序存储，可以这么理解，比如存1234，由于需要十进制进位处理，所以c[0]到c[3]分别是4321 
    }
    for(int i=0;i<len2;i++)
    {
        d[i]=b[len2-1-i]-'0';//同理 
    } 
    int len=max(len1,len2)+1;//防止最后一位出现进位的情况，所以预前多加一位备用 
    int jw=0;//进位 
    int sum[510];
    memset(sum,0,sizeof(sum));
    for(int i=0;i<len;i++)
    {
        sum[i]=c[i]+d[i]+jw;
        jw=sum[i]/10;
        sum[i]=sum[i]%10;
    }
    while(sum[len-1]==0&&len>1)//用来删除前导0，比如我们得出的结果是0123，不需要0，删去就好了，同下面注释的代码 
    len--;
    /*for (int i=len-1; i>=0; i--) {
        if (0==sum[i] && len>1) {
            len--;
        } else {
            break;
        }
    }*/
    for(int i=len-1;i>=0;i--)
    printf("%d",sum[i]);
    return 0;
}

二、高精度减法

题目地址：https://www.luogu.com.cn/problem/P2142

对于高精度减法的储存方式，输出方式以及去前导0的方式是一样的，但不同之处是减法运算需要借位运算，比如：

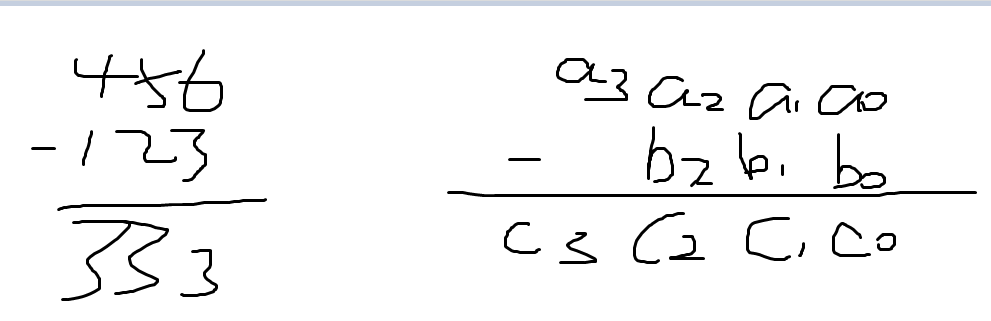
在上图中，我们如果是进行的是顺运算还可以，如果进行借位运算，例：

 123

-98　　我们需要将十位的2减1并且各位的3加10来完成运算。

再有：如果是出现被减数小于减数的情况，就要将被减数和减数互换，完成运算之后加上负号，比如：3-5，3<5，就要互换3与5的位置在相减，得2，在加上负号，得-2；

总结：

1、定义存储数组。

2、被减数和减数确认。并且减法可能出现负数。

3、读入数据到数组中。

4、从个位开始模拟竖式减法的过程，完成整个减法。

5、删除前导 0 。

6、输出减法的结果。

代码以及大多数注释如下：

#include<bits/stdc++.h>
using namespace std;
char a[10090],b[10090];//用来输入大数 
int c[10090],d[10090],sum[10090];//用来存储数据 
char t[10090];//temp变量数组，用来互换两个数组的位置 
int main()
{
    scanf("%s %s",a,b);
    int len1=strlen(a);
    int len2=strlen(b);
    if(len1<len2||len1==len2&&strcmp(a,b)<0)//两个字符串长度不相等或者是相等但是数字有大有小 
    {
        cout<<'-'; 
        strcpy(t,a);
        strcpy(a,b);
        strcpy(b,t);
        len1=strlen(a);//更新长度 
        len2=strlen(b);
    }
    for(int i=0;i<len1;i++)
    {
        c[i]=a[len1-1-i]-'0';//逆序存储，可以这么理解，比如存1234，由于需要十进制进位处理，所以c[0]到c[3]分别是4321 
    }
    for(int i=0;i<len2;i++)
    {
        d[i]=b[len2-1-i]-'0';//同理 
    } 
    for(int i=0;i<len1;i++)
    {
        if(c[i]<d[i])
        {
            c[i+1]--;//借位，高位减一 
            c[i]=c[i]+10;//低位加10 
        }
        sum[i]=c[i]-d[i]; 
        
    } 
    while(sum[len1-1]==0&&len1>1)//用来删除前导0，比如我们得出的结果是0123，不需要0，删去就好了，同下面注释的代码 
    len1--;
    /*for (int i=len-1; i>=0; i--) {
        if (0==sum[i] && len>1) {
            len--;
        } else {
            break;
        }
    }*/
    for(int i=len1-1;i>=0;i--)
    printf("%d",sum[i]);
    return 0;
}

三、高精度乘法

题目地址：https://www.luogu.com.cn/problem/P1303

高精度乘法的难度上一层，其实高精度从加到除的难度一直都是递增的，不说废话了。

其实对于高精度乘法而言，是有迹可循的规律，我们同样可以模拟一下：

通过上图我们可以得到，当a0—b0—c0，

a1—b0—c1      a2-b0-c2     a3-b0-c3,   

a0-b1-c1      a1-b1-c2        a2-b1-c3    a3-b1-c4；

我们分析一下：c[0]=a[0]*b[0],   c[1]=a[1]*b[0]+a[0]*b[1]      c[2]=a[2]*b[0]+a[1]*b[1]     c[3]=a[3]*b[0]+a[2]*b[1]    c[4]=a[3]*b[1];

不难得出 c[i+j]+=a[i]*b[j]，为什么有一个累加的加号呢？其实当初我刚开始接触的时候也是抱有困惑的，也不难理解，就是，拿上面的图来讲，c[1]=a[1]*b[0]+a[0]*b[1] ,列一个舒适不就是a[1]*b[0]+a[0]*b[1]嘛，我画一下：

 

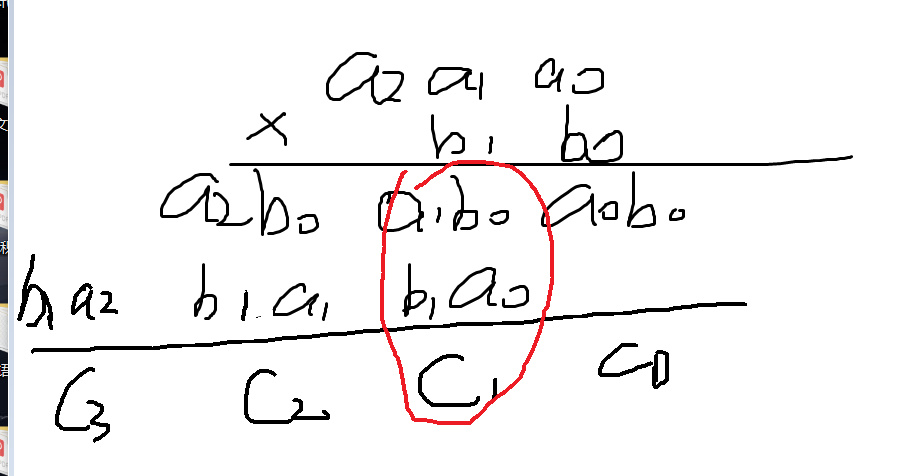
这不就是累加吗，然后在进行错位相加，进位，取余处理，就可以啦。

还有一点，乘积的最大长度是不会超过两个字符串长度之和的，所以定义长度直接让两个字符串的长度相加就可以了。

总结：

1、定义存储数组。

2、读入数据处理。

3、从个位开始模拟竖式乘法的过程，完成整个乘法。

4、删除前导 0 。

5、输出结果。

代码及注意事项如下：

#include<bits/stdc++.h>
using namespace std;
char a[2010],b[2010];//用来输入大数 
int c[2010],d[2010];//用来存储数据 
int sum[4020];//为什么用4020的长度呢，因为相乘之后数据的长度翻倍，这是我亲爱的老师告诉我的，嘻嘻 
int main()
{
    scanf("%s %s",a,b);
    int len1=strlen(a);
    int len2=strlen(b);
    int len3=len1+len2;//乘积的总长度是不会超过两个长度之和的 
    for(int i=0;i<len1;i++)
    {
        c[i]=a[len1-1-i]-'0';//逆序存储，可以这么理解，比如存1234，由于需要十进制进位处理，所以c[0]到c[3]分别是4321 
    }
    for(int i=0;i<len2;i++)
    {
        d[i]=b[len2-1-i]-'0';//同理 
    } 
    for(int i=0;i<len1;i++)
    {
        for(int j=0;j<len2;j++)
        {
            sum[i+j]+=c[i]*d[j];//细细体会
            sum[i+j+1]+=sum[i+j]/10;//进位
            sum[i+j]%=10;//每位超不过10 
        }
    } 
    while(sum[len3-1]==0&&len3>1)//用来删除前导0，比如我们得出的结果是0123，不需要0，删去就好了，同下面注释的代码 
    len3--;
    /*for (int i=len-1; i>=0; i--) {
        if (0==sum[i] && len>1) {
            len--;
        } else {
            break;
        }
    }*/
    for(int i=len3-1;i>=0;i--)
    printf("%d",sum[i]);
    return 0;
}

另外，高精度乘法要特别感谢我的老师，要不是我的老师对我进行了及时的指导和纠正，我高精度乘法就有可能卡一下午（加晚上）

四、高精度除法

高精度除法是分两个部分的其实，分别是高精度除以低精度（难度稍微较小），高精度除以高精度（难度较大且代码较为繁琐，新手不建议入手）

小声bb:虽然我是学的c,但是python自带高精度真好用，2，3行代码搞定┭┮﹏┭┮；

(1).高精度除低精度

题目链接：https://www.luogu.com.cn/problem/P1480

高精度除以低精度不太好总结说实话，但是要进行一下复盘还是总结一下吧，毕竟在脑子中过一遍还是比不过要好的；

为什么要拿这个题来做高单除的例题，高高除不行吗？高高除可以，但是这个题的数据范围要注意：

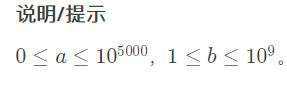
被除数比除数大的多并且被除数很大而除数相对来说较小，在long long的范围之中，所以可以用高单除；

我们首先分析，在我们日常中是怎么计算除法的，我们来模拟一下：

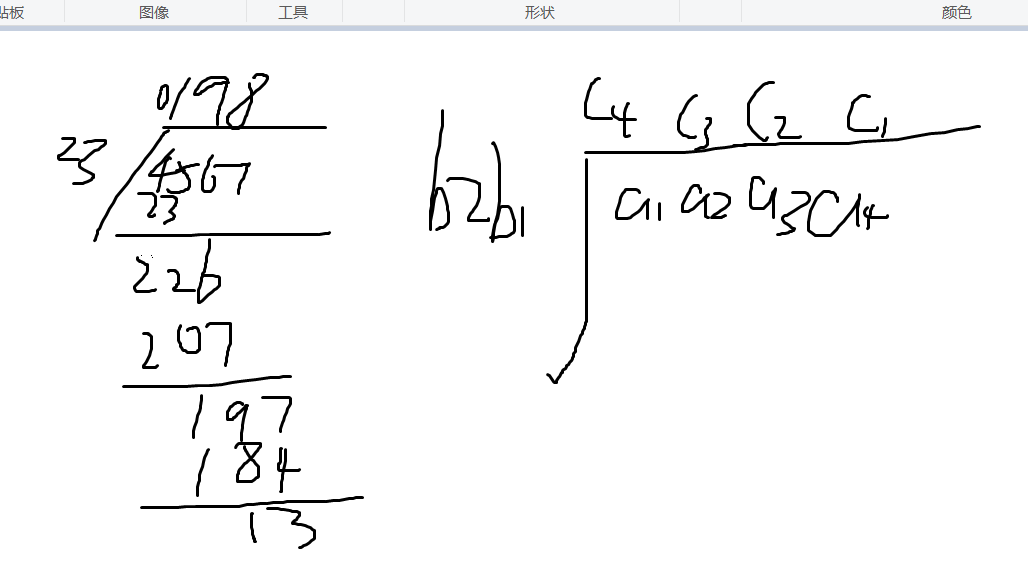
我们采取的是逐位试商的方法，拿上图来说，4567/23，首先是4/23，商0余4，45/23商2余22，226/23.....一直到197/23商9余13。这就是逐位试商的模拟过程。

也如这样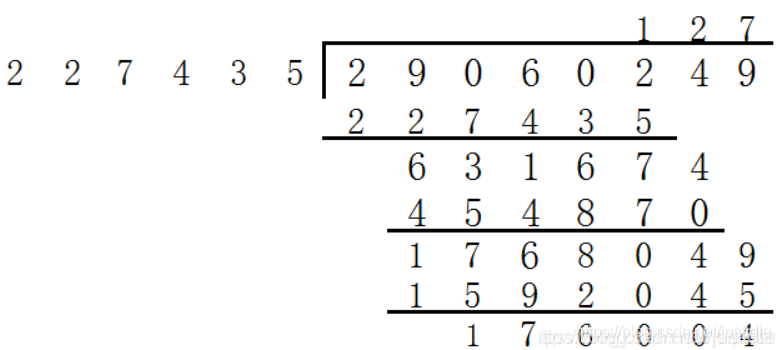

但是很显然，计算机并不能进行逐位试商的方法，所以，我们需要对计算机进行减法模拟

并且我们要注意，除法不同于加法和减法还有乘法，我们把存储方式改为正序存储即可，并且要注意在定义长度的时候要用long long，要不然可能会造成数据错误导致WA（亲身实践）；

试商过程：
1、将除数移动和被除数对齐，位数不够时，补 0。

2、利用被除数减去除数，一直减到被除数小于除数，减的次数，就是“试商”的结果，每移动一次。

3、重复上述步骤，一直到被除数和除数的位数相等为止。

举例说明：
举一个例子，比如 524134 除以 123，结果是 4261 ，余数为 31。

1、第一位 4 的来源是我们把 524 和 123 对齐，然后进行循环减法，循环了 4 次，余 32；

2、将 32134 的前三位 321 继续和 123 对齐，循环减法 2 次，余 75；

3、把 7534 的前三位 753 和 123 对齐，循环减法 6 次，余 15；

4、将 154 和 123 对齐，只能减 1 次，余 31。

所以 524134 除以 123，结果是 4261，余数为 31。

上面思路借鉴自一位大佬，真的犇，不得不服。

总结

1、定义存储数组。

2、读入数据处理，正序存储

3、试商过程。

4、删除前导 0 ，正序删除，从sum【0】开始一旦发现是0就停止并且长度要小于len1；

5、输出结果。

代码及注意事项如下：

#include<bits/stdc++.h>
using namespace std;
char a[5010];//用来存储数据
int c[5010];//转化 
long long b,x; //注意用long long  
int sum[5010];
int main()
{
    scanf("%s %lld",a,&b);
    long long len1=strlen(a);
    for(int i=0;i<len1;i++)
    {
        c[i]=a[i]-'0';//正序储存即可，从高位往低位逐步试商就可以了 
    }
    for(int i=0;i<len1;i++)
    {
        sum[i]=(x*10+c[i])/b;//每次和除数相除得到商 ，不断试商保存在sum[i]里， 
        x=(x*10+c[i])%b;//余数 
    }
    long long len2=0 ;//用longlong定义并且正序开始遍历 
    while(sum[len2]==0&&len2<len1)//用来删除前导0，比如我们得出的结果是0123，不需要0，删去就好了，同下面注释的代码 
    len2++;
    /*for (int i=len-1; i>=0; i--) {//即使根据题意做出调整，不写了 
        if (0==sum[i] && len>1) {
            len--;
        } else {
            break;
        }
    }*/
    for(int i=len2;i<len1;i++)//正序输出 
    printf("%d",sum[i]);
    return 0;
}

（2）.高精度除以高精度

这么嘛，掌握的不是很熟，完全掌握之后在总结吧。