洛谷P1094 [NOIP2007 普及组] 纪念品分组

1|0题目描述

元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品， 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。

你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。

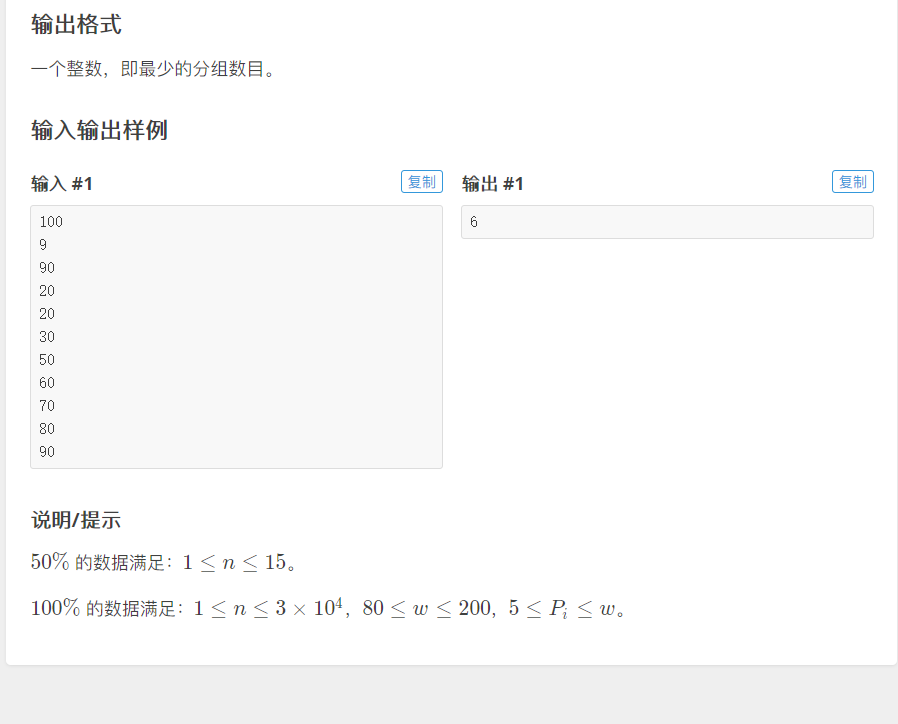
2|0输入格式

共 n+2 行：

第一行包括一个整数 w，为每组纪念品价格之和的上上限。

第二行为一个整数 n，表示购来的纪念品的总件数 G。

第 3∼n+2 行每行包含一个正整数 pi 表示所对应纪念品的价格。

 

 很典型的贪心问题，要想让分组最少就要尽量让大的和小的凑在一起满足临界值，实在盛不下的只能单独装一组；

代码如下：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int w,n;
    scanf("%d",&w);
    int a[30010];
    memset(a,0,sizeof(a));
    cin>>n;
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
        }
        sort(a,a+n);
        int j=0;
        int k=n-1;
        int sum=0;
        while(j<=k)
        {
            if(a[j]+a[k]<=w)
            {
                sum++;
                j++;
                k--;
            }else
            {
                sum++;
                k--;
            }
        }
        printf("%d",sum);
    return 0;
}

但是还有应该反思的地方，就是如何证明贪心问题，借用大佬的话就是：贪心算法不难，但证明难；

这里借鉴大佬的博客，对大佬真的是膜拜：https://www.luogu.com.cn/blog/heidoudou/solution-p1094

__EOF__

本文作者：江上舟摇
本文链接：https://www.cnblogs.com/LQS-blog/p/15866250.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！