洛谷P1090 [NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 n-1n−1 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 11 ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 33 种果子，数目依次为 11 ， 22 ， 99 。可以先将 11 、 22 堆合并，新堆数目为 33 ，耗费体力为 33 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 1212 ，耗费体力为 1212 。所以多多总共耗费体力 =3+12=15=3+12=15 。可以证明 1515 为最小的体力耗费值。

输入格式

共两行。
第一行是一个整数 n(1≤n≤10000) ，表示果子的种类数。

第二行包含 nn 个整数，用空格分隔，第 i 个整数 ai​(1≤ai​≤20000) 是第 i 种果子的数目。

输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 2^31

 

 这个题我觉得很经典，我先写一下流程：

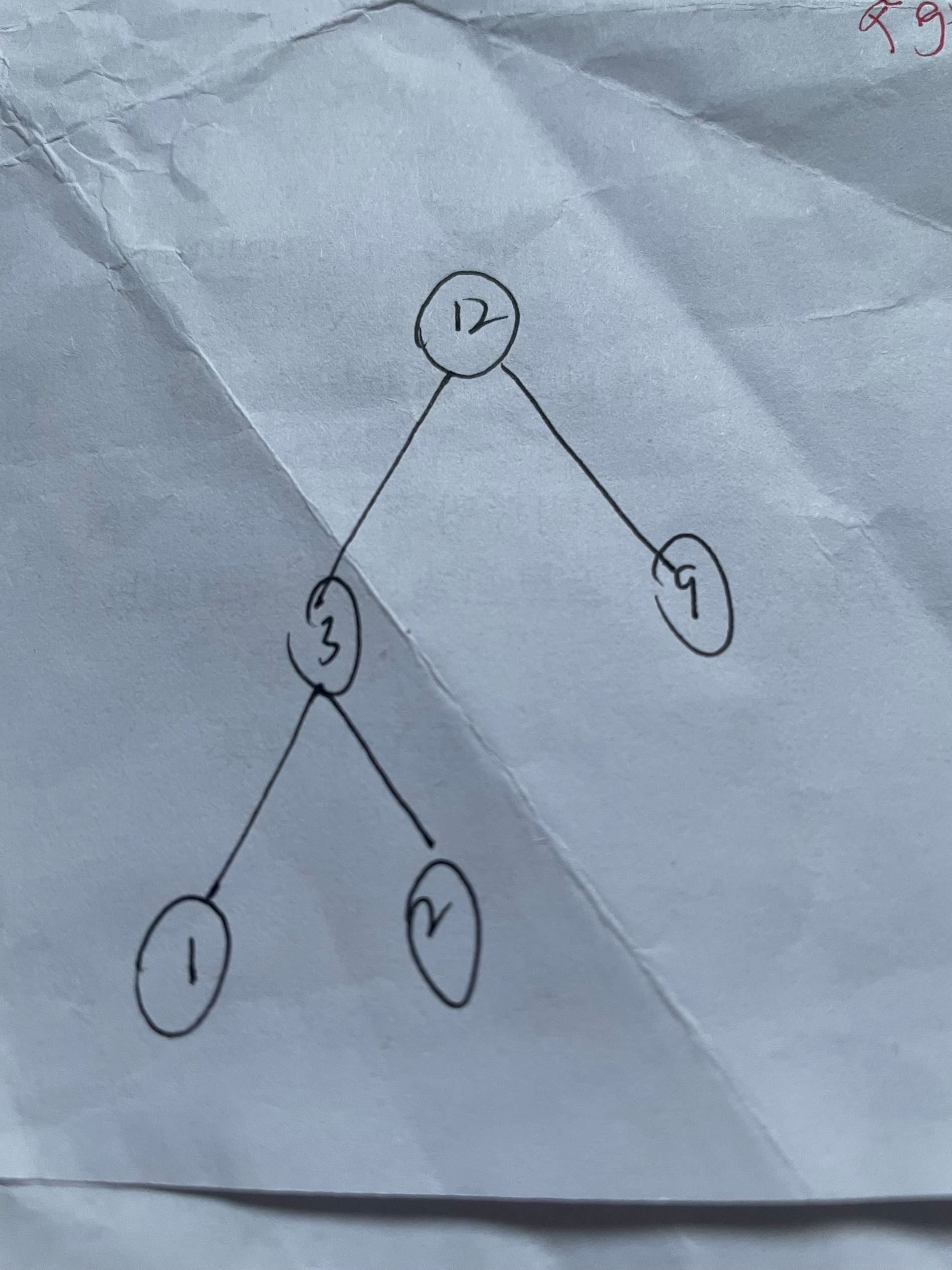
明白了吧，很经典的哈夫曼，直接用哈夫曼的套路解决就可以了，

ac代码如下，注释我也不多写了：

#include<bits/stdc++.h>
using namespace std;
int a[10010];
int main()
{
    int sum=0,n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
        
    }
    int j=0;
    sort(a,a+n);
    while(j<n-1)
    {
        sum+=(a[j]+a[j+1]);
        a[j+1]=a[j]+a[j+1];
        j++;
        sort(a+j,a+n);
    }
    printf("%d",sum);
    return 0;
}