洛谷P2240 【深基12.例1】部分背包问题（经典模板）

 

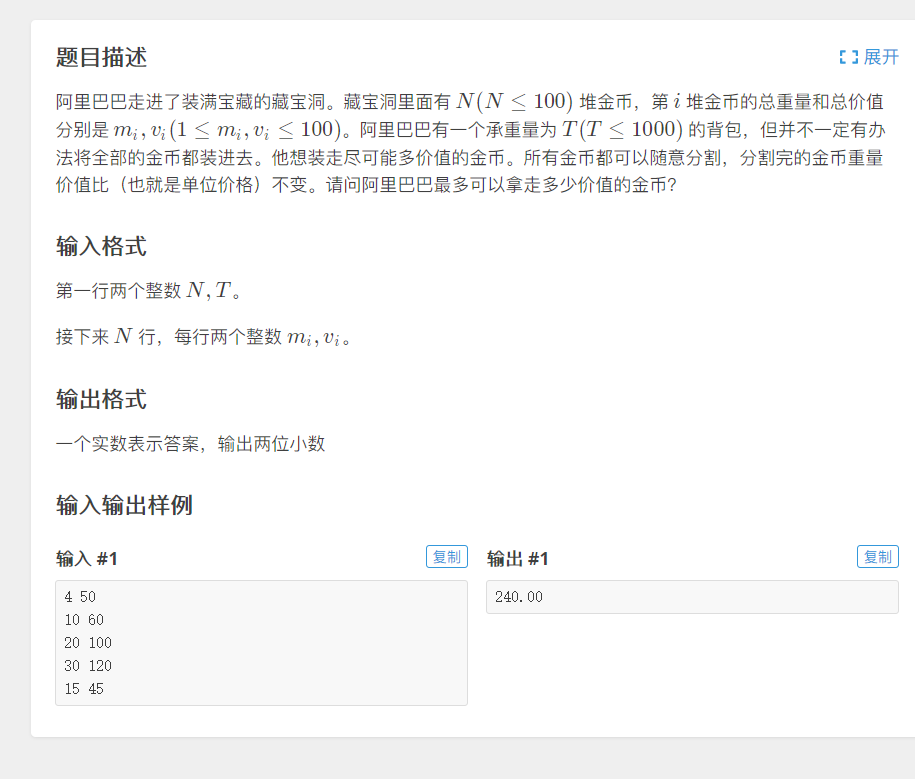
 首先应该注意几个关键信息：装走尽多的金币、所有金币可以随意分割并且分割后金币的价值比不变;

我们可以抽象成一个买东西的场景，给你一定数目的钱，让你在这些钱内尽量在超市买更多的小零食，这就牵扯到了一个性价比的问题。

那如此，这个题目就好解决了，就用这个背包尽量装更多的金币，如果可以装的下，那就装好了，毕竟谁不喜欢钱呢；

那如果装不下呢（对于第i堆金币）？

这个就可以把金币分割了，在剩下的背包容量中装可以装满的金币，用它的装载量去乘金币的价值比，就是所获得的金币的量；

代码如下：

#include<bits/stdc++.h>
using namespace std;
struct node
{
    int  value;
    int weight;
    double cp;//cost performence性价比 
}coin[110];
bool cmp(node x,node y)
{
    return (x.cp>y.cp);
}
int main()
{
    int n,t;
    cin>>n>>t;
    for(int i=0;i<n;i++)
    {
        scanf("%d %d",&coin[i].weight,&coin[i].value);
        coin[i].cp=(double)coin[i].value/coin[i].weight;//类型转换 
    }
    sort(coin,coin+n,cmp);//性价比降序排序 
    double sum=0;
    for(int i=0;i<n;i++)
    {
        if(t>=coin[i].weight)
        {
            sum+=coin[i].value;
            t-=coin[i].weight;
        }
        else
        {
            sum+=t*coin[i].cp;
            break;//不要忘记break 
        }
    }
    printf("%.2f",sum);
    return 0;
    
 }