datawhale-动手学图深度学习task04
动手学图深度学习
图表示学习
研究在嵌入空间(Embedding Space,指在高维数据被映射到低维空间的数学结构)表示图的方法,在图上表示学习核嵌入指的是同一件事,“嵌入”是指将网络中的每个节点映射到低维空间(需要深入了解节点的相似性和网络结构),旨在捕捉图结构中的拓扑信息、节点内容信息以及边的类型和权重。
节点表示学习
-
节点嵌入的目标是对节点进行编码,使得嵌入空间中的相似性近似于原始网络中的相似性。
-
节点嵌入算法通常有三个基本阶段组成:
- 定义一个编码器(即从节点到嵌入的映射)。
- 定义节点相似度函数(用于评估图中两个节点相似性或相关性的函数),保持原始网络节点间关系在向量空间中关系不变。
- 优化编码器的参数,使得节点间的关系在嵌入空间中得到最优保持。
-
两种节点嵌入方法:
- 深度游走;
- Node2Vec
-
一般的随机游走:深度游走
-
随机游走:
给定一个图和一个起点,随机选择一个邻居,并移动到这个邻居,然后随机选择该点的邻居,并移动它,以此类推; -
图上的随机游走是以这种方式选择的点的序列;
-
深度游走算法特指运行固定长度、无偏的随机游走:
从节点\(u\)开始采用随机游走策略\(R\)进行游走,得到附近的节点\(N_R(u)\),我们希望嵌入空间中使得附近的节点嵌入相似度高,所以需要优化嵌入以最大化随机游走共现(在随机游走生成的路径中频繁共现的节点在嵌入空间中也彼此接近)的可能性,其损失函数为:\[\mathcal{L}=\sum_{u \in V} \sum_{v \in N_{R}(u)}-\log \left(\frac{\exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{v}}\right)}{\sum_{\mathrm{n} \in \mathrm{V}} \exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{n}}\right)}\right) \]因为优化这个函数的代价太大,于是我们需要计算分母中每两个节点的相似度,可以用负采样(选择少量的负例计算随机估计其他节点)简化计算:
\[\mathcal{L}=\sum_{u \in V} \sum_{v \in N_{R}(u)}-\log \left(\frac{\exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{v}}\right)}{\sum_{\mathrm{n} \in \mathrm{V}} \exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{n}}\right)}\right)\log \left(\frac{\exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{v}}\right)}{\sum_{\mathrm{n} \in \mathrm{V}} \exp \left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{n}}\right)}\right) \approx \log \left(\sigma\left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{v}}\right)\right)-\sum_{\mathrm{i}=1}^{\mathrm{k}} \log \left(\sigma\left(\mathbf{z}_{\mathbf{u}}{ }^{\mathrm{T}} \mathbf{z}_{\mathbf{n}_{\mathbf{i}}}\right)\right), \mathrm{n}_{\mathrm{i}} \sim \mathrm{P}_{\mathrm{v}} \]
这里的损失函数是噪声对比估计(NCE)的一种新是,可使用逻辑回归(sigmoid函数)近似最大化softmax的对数概率,较高的\(k\)能给出更鲁棒的估计,通常选择的值在5~20之间。
-
-
有偏的随机游走:Node2Vec
-
深度游走太死板,会限制表征的学习,而Node2Vec通过图上的BFS和DFS在网络的局部视图和全局视图间权衡;
-
BFS可以给出邻域的局部微观视图,DFS提供邻域的全局宏观视图;
-
返回参数\(p\)来代表游走着返回前一个节点的转移概率,当\(p\)的值比较大的时候,Node2Vec像BFS,当\(p\)的值比较小的时候,Node2Vec像DFS(即q控制游走);
-
输入输出参数\(q\)定义BFS和DFS的“比率”,q较小,游走者更倾向于探索与当前节点远的节点(DFS)。如果q较大,游走者更倾向于探索与当前节点近的节点(BFS)。
-
游走者从当前节点\(v\)出发,选择下一个节点\(x\)的概率\(w(v,x)\):
\[w(v,x) = \left\{ \begin{array}{ll} \frac{1}{p} & d_{uv} = 0 \\[5pt] 1 & d_{uv} = 1 \\[5pt] \frac{1}{q} & d_{uv} = 2 \\[5pt] \end{array} \right. \]\(d_{uv}\)表示节点\(u\)和节点\(v\)之间的最短路径长度;
\(d_{uv}=0\)代表访问过的节点;
\(d_{uv}=1\)代表访问节点与当前节点直接相连的节点;
\(d_{uv}=2\)代表与当前节点距离为2的节点;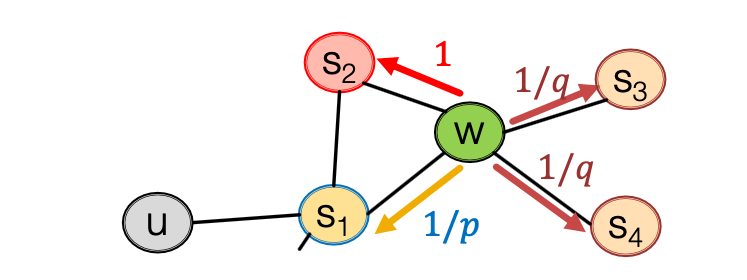
- Node2Vec算法:
- 计算随机游走概率;
- 模拟\(r\)个节点从节点\(u\)开始长度为\(l\)的随机游走;
- 使用随机梯度下降优化Node2Vec游走。
-
图表示学习
-
用数据集的标签来直接监督(指导)两两节点的嵌入,例如边分类问题通过最大化正边的两个节点的点积可以学习到一个很好的嵌入。
-
示例:通过边分类为正负(有无),来完成一个节点嵌入学习:
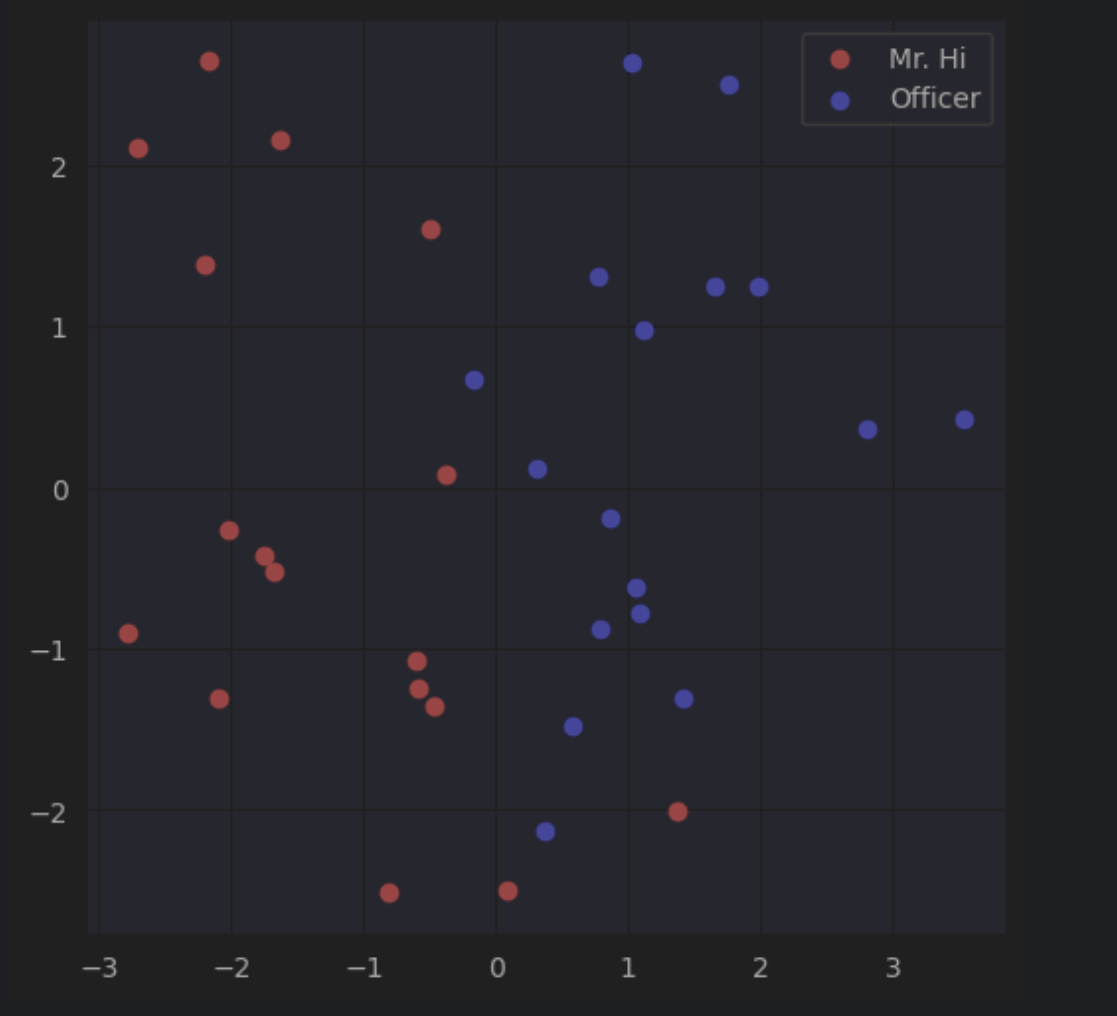
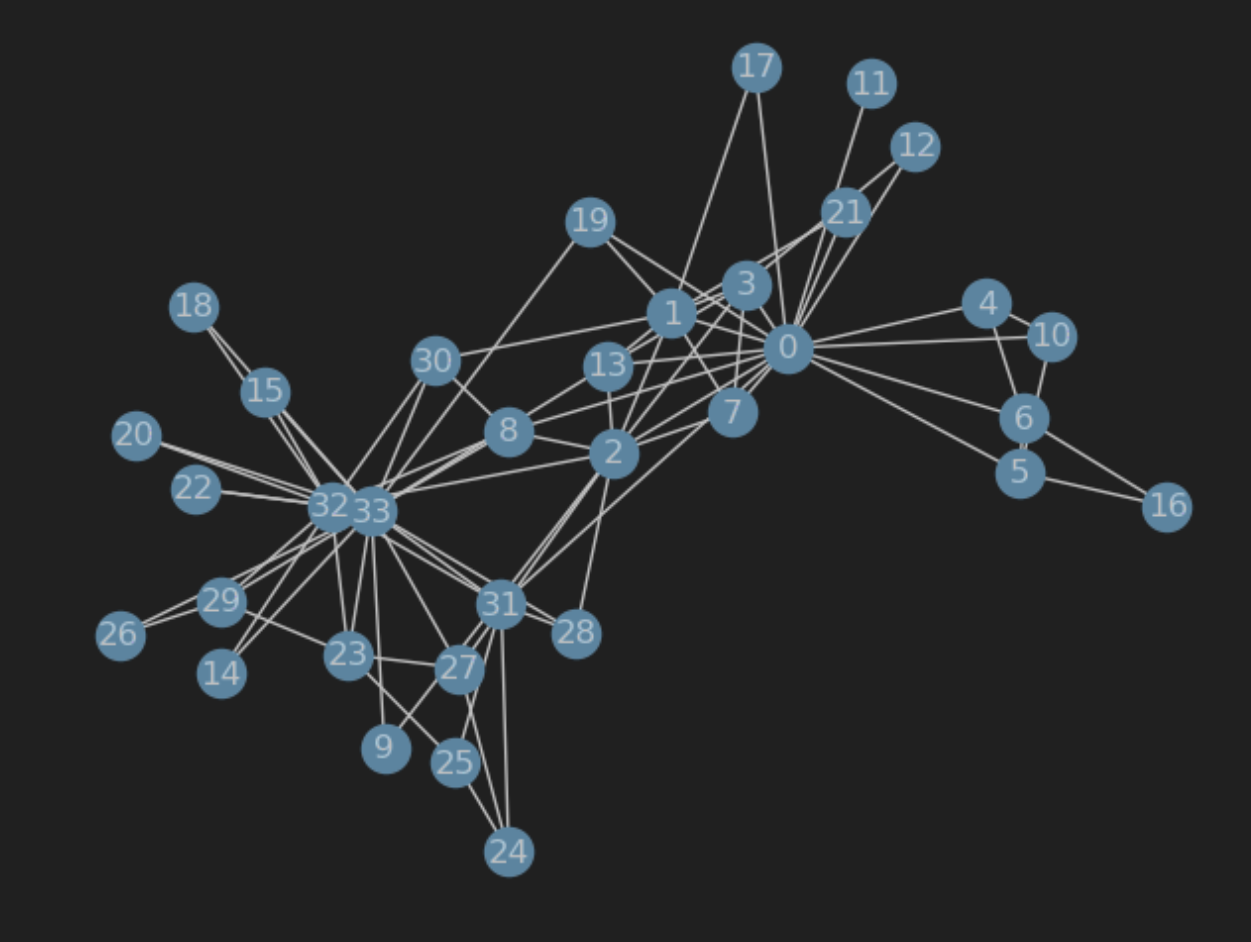
import networkx as nx import torch import torch.nn as nn from torch.optim import SGD import matplotlib.pyplot as plt from sklearn.decomposition import PCA import random # 载入空手道俱乐部网络 G = nx.karate_club_graph() # 可视化图 nx.draw(G, with_labels = True) torch.manual_seed(1) '''可视化随机初始化嵌入: 每个节点都有16维向量,初始化均匀分布矩阵''' # 初始化嵌入函数 def create_node_emb(num_node=34, embedding_dim=16): emb=nn.Embedding(num_node,embedding_dim) # 创建 Embedding(这是一种将离散对象映射到连续空间向量的技术,保持对象之间的相似性和关系,使得在连续空间中,相似的对象靠得近,而不相似的对象则相隔远) emb.weight.data=torch.rand(num_node,embedding_dim) # 均匀初始化 return emb # 初始化嵌入 emb = create_node_emb() # 可视化 def visualize_emb(emb): X = emb.weight.data.numpy() pca = PCA(n_components=2) components = pca.fit_transform(X) plt.figure(figsize=(6, 6)) club1_x = [] club1_y = [] club2_x = [] club2_y = [] for node in G.nodes(data=True): if node[1]['club'] == 'Mr. Hi': #node的形式:第一个元素是索引,第二个元素是attributes字典 club1_x.append(components[node[0]][0]) club1_y.append(components[node[0]][1]) #这里添加的元素就是节点对应的embedding经PCA后的两个维度 else: club2_x.append(components[node[0]][0]) club2_y.append(components[node[0]][1]) plt.scatter(club1_x, club1_y, color="red", label="Mr. Hi") plt.scatter(club2_x, club2_y, color="blue", label="Officer") plt.legend() plt.show() # 可视化初始嵌入 visualize_emb(emb) '''分类存放正边和负边''' # 处理正边 def graph_to_edge_list(G): # 将 tensor 变成 edge_list edge_list = [] for edge in G.edges(): edge_list.append(edge) return edge_list def edge_list_to_tensor(edge_list): # 将 edge_list 变成 tesnor edge_index = torch.tensor([]) edge_index=torch.LongTensor(edge_list).t() return edge_index pos_edge_list = graph_to_edge_list(G) pos_edge_index = edge_list_to_tensor(pos_edge_list) # 处理负边(负边采样) def sample_negative_edges(G, num_neg_samples): neg_edge_list = [] # 得到图中所有不存在的边(这个函数只会返回一侧,不会出现逆边) non_edges_one_side = list(enumerate(nx.non_edges(G))) neg_edge_list_indices = random.sample(range(0,len(non_edges_one_side)), num_neg_samples) # 取样num_neg_samples长度的索引 for i in neg_edge_list_indices: neg_edge_list.append(non_edges_one_side[i][1]) return neg_edge_list # 78个负边样本 neg_edge_list = sample_negative_edges(G, len(pos_edge_list)) # 负边转换为tensor neg_edge_index = edge_list_to_tensor(neg_edge_list) '''2''' def accuracy(pred, label): #输入参数: # pred (the resulting tensor after sigmoid) # label (torch.LongTensor) #预测值大于0.5被分类为1,否则就为0 #准确率返回值保留4位小数 #accuracy=预测与实际一致的结果数/所有结果数 #pred和label都是[78*2=156]大小的Tensor accu=round(((pred>0.5)==label).sum().item()/(pred.shape[0]),4) return accu def train(emb, loss_fn, sigmoid, train_label, train_edge): #题目要求: #用train_edge中的节点获取节点嵌入 #点乘每一点对的嵌入,将结果输入sigmoid #将sigmoid输出输入loss_fn #打印每一轮的loss和accuracy epochs = 500 learning_rate = 0.1 optimizer = SGD(emb.parameters(), lr=learning_rate, momentum=0.9) for i in range(epochs): optimizer.zero_grad() train_node_emb = emb(train_edge) # [2,156,16] # 156是总的用于训练的边数,指78个正边+78个负边 dot_product_result = train_node_emb[0].mul(train_node_emb[1]) # 点对之间对应位置嵌入相乘,[156,16] dot_product_result = torch.sum(dot_product_result,1) # 加起来,构成点对之间向量的点积,[156] sigmoid_result = sigmoid(dot_product_result) # 将这个点积结果经过激活函数映射到0,1之间 loss_result = loss_fn(sigmoid_result,train_label) loss_result.backward() optimizer.step() if i%10==0: print(f'loss_result {loss_result}') print(f'Accuracy {accuracy(sigmoid_result,train_label)}') loss_fn = nn.BCELoss() sigmoid = nn.Sigmoid() # 生成正负样本标签 pos_label = torch.ones(pos_edge_index.shape[1], ) neg_label = torch.zeros(neg_edge_index.shape[1], ) # 拼接正负样本标签 train_label = torch.cat([pos_label, neg_label], dim=0) # 拼接正负样本 # 因为数据集太小,我们就全部作为训练集 train_edge = torch.cat([pos_edge_index, neg_edge_index], dim=1) train(emb, loss_fn, sigmoid, train_label, train_edge) # 训练后可视化 visualize_emb(emb)最初的关系图
最初未优化的嵌入图
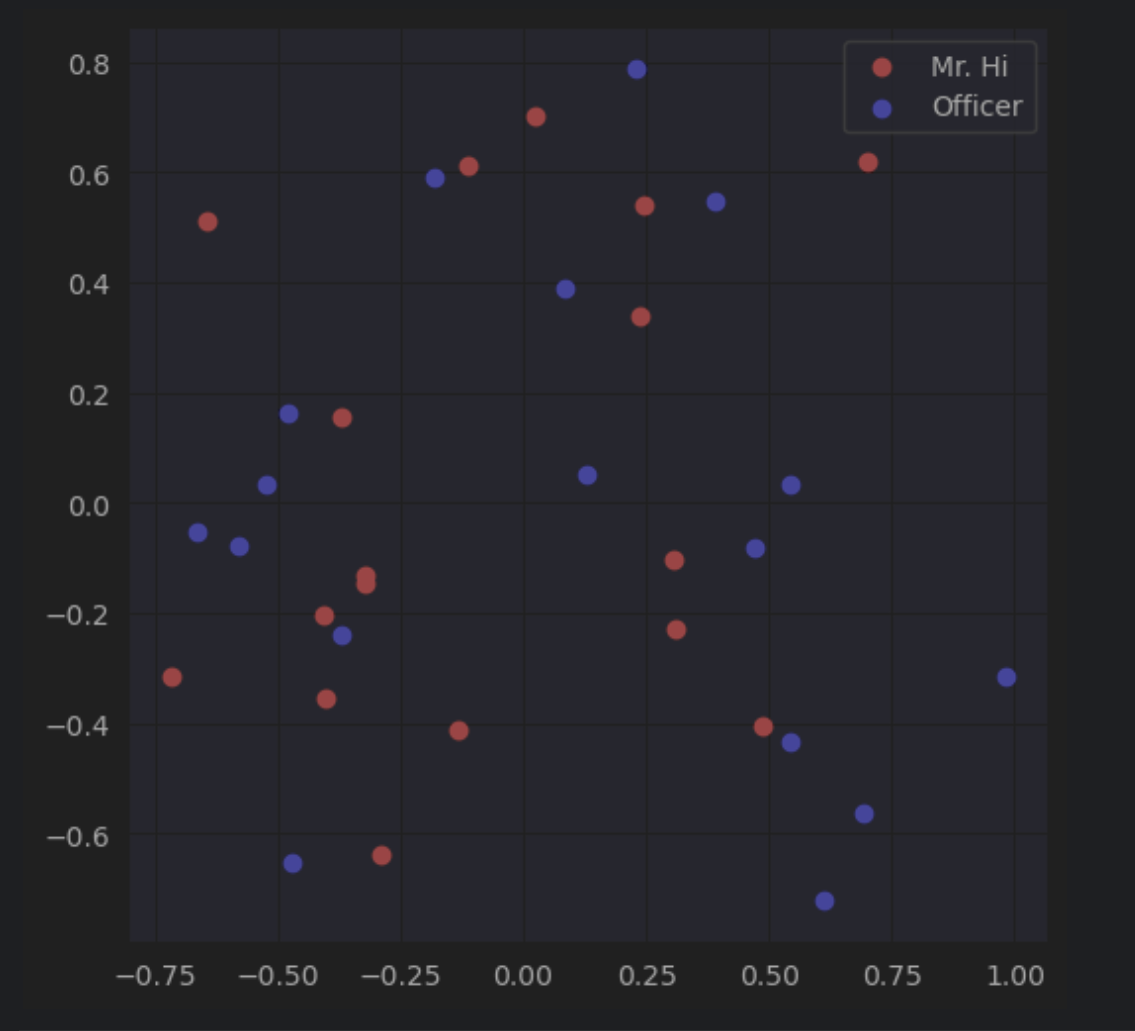
优化后的嵌入图