datawhale-动手学图深度学习task03

动手学图深度学习

声明：本文是在笔者的Pytorch tutorial及深度学习入门(鱼书)笔记的基础上继续学习记录，故有些内容略过。

第三章：深度学习基础

神经网络及其基本组成的补充

1. 欠拟合：

   训练误差和验证误差都很严重，而且他们间仅有一点差距，如果模型不能降低训练误差，这可能是因为模型过于简单（即表达能力不足），无法捕获试图学习的模式。

2. 权值衰减补充：

   • L2正则化线性模型构成经典的岭回归(ridge regression)算法；
   • L1正则化线性回归是统计学中类似的基本模型，通常被称为套索回归(lasso regression)。
   • L1正则化是在原始损失函数上增加一个惩罚项L1范数来实现的，即权重的绝对值之和。
   • L1正则化的特点：
     • 倾向于产生稀疏的权重矩阵，即倾向于将一些特征的权重减少到0（这里是常数倍惩罚，而L2是权重平方所以不太可能减小到0）。
     • 基于权重的大小进行惩罚，对异常值的影响较小。
     • 计算简单。

卷积神经网络的补充

1. CNN具有的特性：

   • 平移不变性(translation invariance)：
     不管检测对象出现在图像中的哪个位置，神经网络的前基层应该对相同的图像区域具有相似的反映。图像的平移不变性使我们以相同的方式处理局部图像，而不在乎它的位置；
   • 局部性(locality)：
     神经网络的前几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，最终，可以聚合这些局部特征，以整个图像级别进行预测。局部性意味着计算相应的隐藏只需一小部分局部图像像素。

2. 特征映射与感受野：

   • 输出的卷积层有时称为特征映射(feature map)，因为它可以被视为一个输入映射到下一层的空间维度的转换器。
   • 感受野是指在前向传播期间可能影响计算的所有元素，更具体的是神经网络中神经元“看到的”输入区域，即feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。

循环神经网络RNN

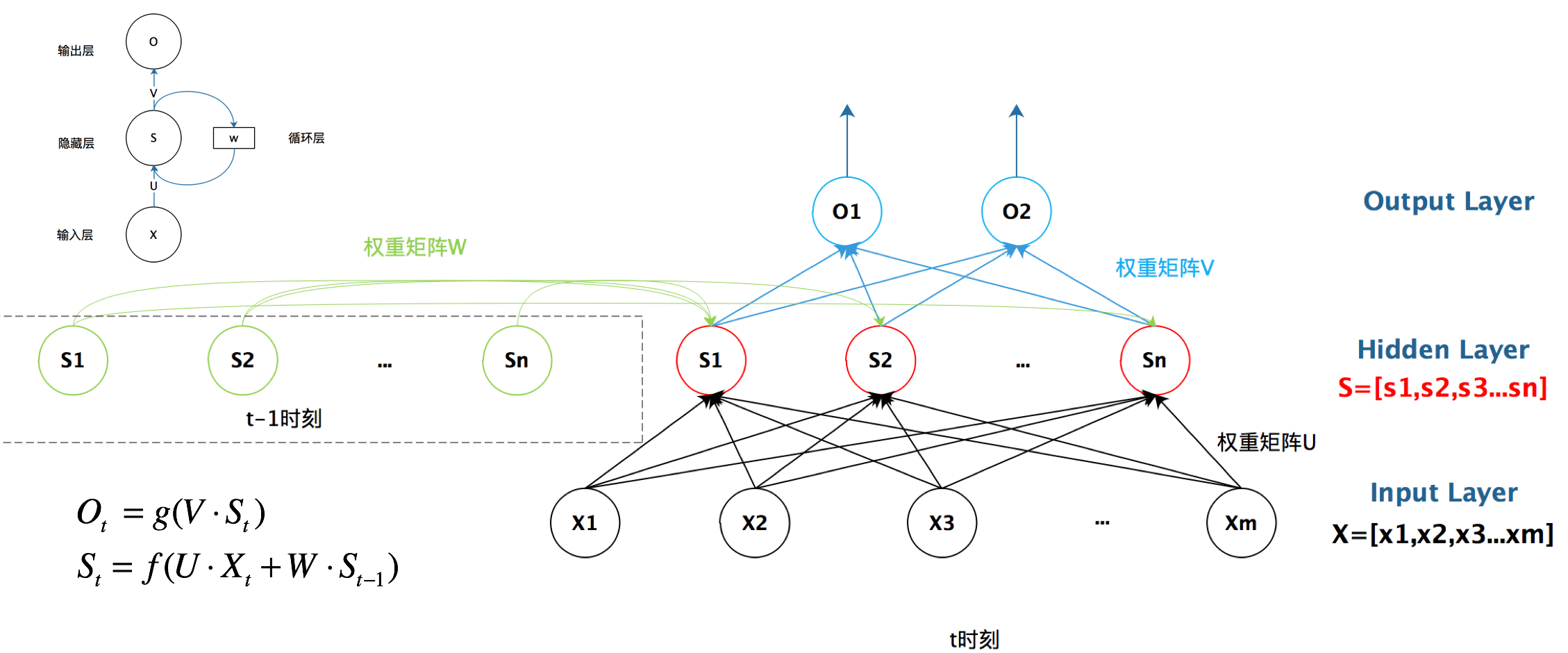
循环神经网络是一种在序列数据上进行建模的神经网络模型，该模型相较传统网络具有循环连接，可以将前面的信息传递到后面的步骤中，从而捕捉到序列数据中的时序关系。

1. 相较于普通神经网络结构，RNN多了一个隐藏权重矩阵W。在RNN中，隐藏层的值不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值，而权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。

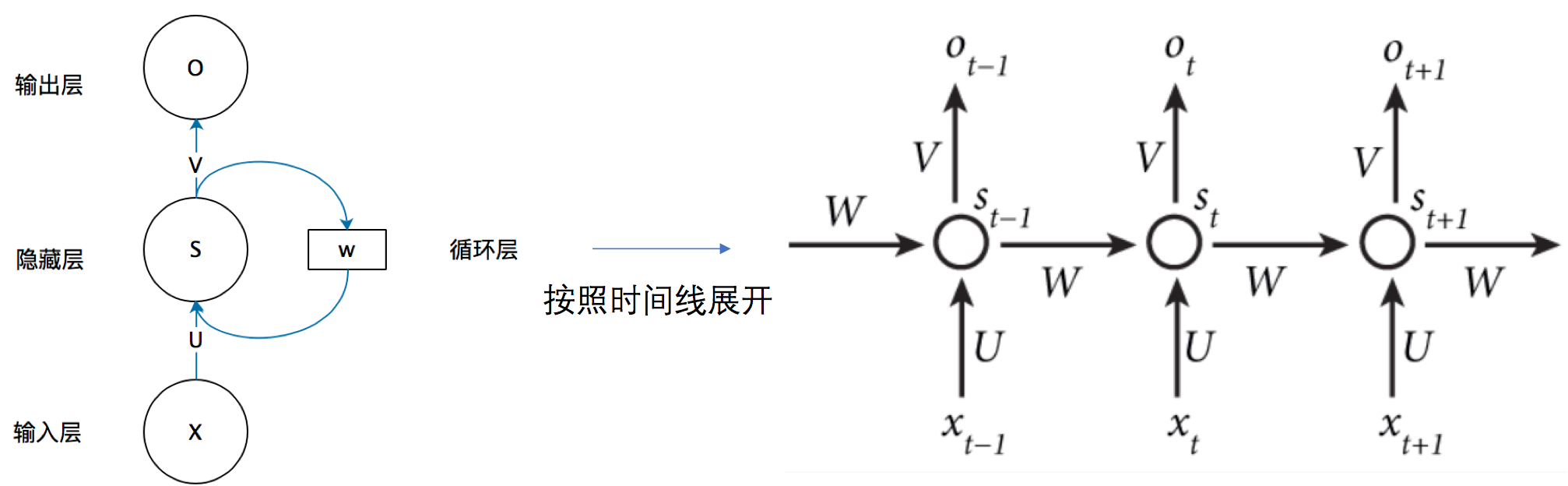
2. 这是通俗理解的结构图：
   

3. RNN中相关概念：

   • 隐藏变量(隐藏状态、hidden state)：指网络中用于存储序列历史信息的内部变量，一般会在每个时间步长更新，并把它的值当作下一个时间步长的输入之一。

   • 隐藏变量的更新公式：

     \[h_t = \phi(W_h \cdot h_{t-1} + W_x \cdot x_t + b_h) \]
     • \(h_t\) 是时间步长 \(t\) 的隐藏状态。
     • \(h_{t-1}\) 是前一个时间步长 \(t-1\) 的隐藏状态。
     • \(x_t\) 是当前时间步长 \(t\) 的输入。
     • \(W_h\) 和 \(W_x\) 是权重矩阵，分别表示隐藏状态和输入的权重。
     • \(b_h\) 是偏置向量。
     • \(\phi\) 是激活函数，如tanh或ReLU。

   • 隐藏状态使用的定义与前一个时间步中使用的定义相同，因此这种计算是循环的，所以基于循环计算的隐藏状态神经网络被命名维循环神经网络(recurrent neural network)，在RNN中执行计算的层称为循环层(recurrent layer)。

4. RNN的经典变体包括长短期记忆网络(Long Short-Trem Memory, LSTM)和门控循环单元(Gated Recurrent Unit, GRU).

5. RNN代码实现：

   # Define the RNN model
   class RNN(nn.Module):
       def __init__(self, input_size, hidden_size, num_layers, num_classes):
           super(RNN, self).__init__()
           self.hidden_size = hidden_size
           self.num_layers = num_layers
           self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
           self.fc = nn.Linear(hidden_size, num_classes)
   
       def forward(self, x):
           h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
           out, _ = self.rnn(x, h0)
           out = self.fc(out[:, -1, :])
           return out
   
   # Initialize the model
   model = RNN(input_size, hidden_size, num_layers, num_classes)
   

结尾

本文参考文档及图片来自一文搞懂RNN（循环神经网络）基础篇及Grape Book第三章。