datawhale-动手学数据分析task5笔记
datawhale-动手学数据分析task5笔记
模型搭建和评估--建模
模型搭建前的准备
-
引入所需的库与数据。
-
对数据进行特征工程:从原始数据中提取有用的特征,以便机器学习算法能够更有效地进行学习和预测。
-
数据集导致模型在拟合数据时发生变化的常见差异:
-
特征差异
-
样本数量与分布差异
-
噪声与异常值
-
目标变量差异
-
数据划分差异
-
时间序列数据的时序差异
-
数据预处理与清洗
-
模型搭建
sklearn的算法选择路径图:
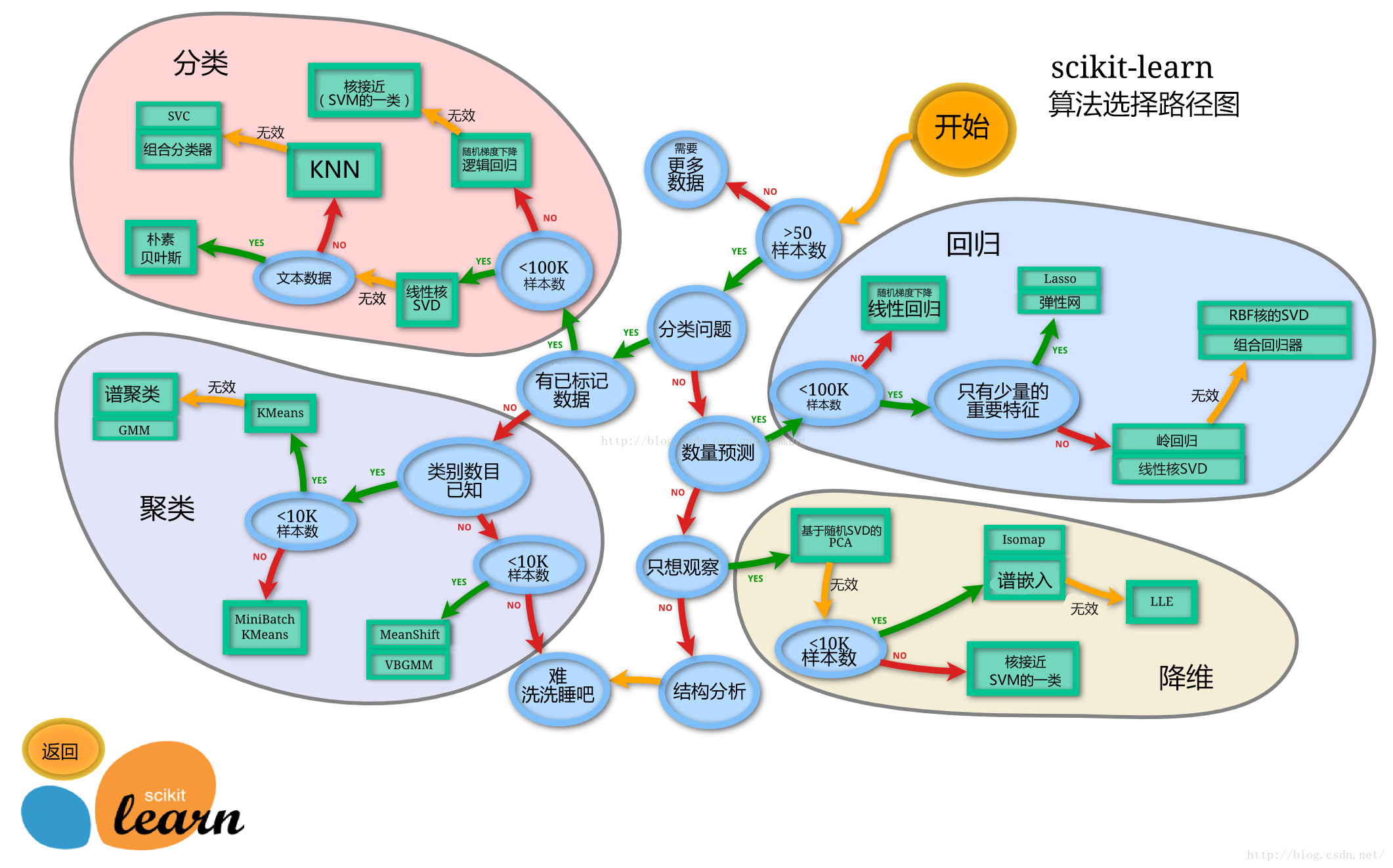
切割训练集和测试集
-
划分数据集的方法:
-
简单随机抽样(Simple Random Sampling):
从总体中随机选择样本,每个样本被选中的概率是相等的。
适用于没有先验知识或特定结构的数据集。 -
分层抽样(Stratified Sampling):
根据某个或多个特征将数据分成不同的层或子集,然后从每层中随机抽取样本。
常用于确保每个类别的样本在训练集、验证集和测试集中都有合适的比例。 -
时间序列划分:
对于时间序列数据,通常按照时间顺序划分数据集,如使用前80%的数据作为训练集,接下来的10%作为验证集,最后的10%作为测试集。
这种划分方式有助于保持数据的时间依赖性,并防止未来数据泄露到训练集中。 -
K折交叉验证(K-fold Cross-validation):
将数据集分成K个不相交的子集,每次使用K-1个子集作为训练集,剩下的一个子集作为验证集。
这个过程重复K次,每次使用不同的子集作为验证集。
最后,对K次验证的结果取平均值,得到模型的性能估计。 -
留出法(Hold-out):
将数据集随机划分为两个互斥的子集,一个作为训练集,另一个作为测试集。
训练集用于训练模型,测试集用于评估模型的性能。
这种方法简单且易于实现,但可能由于随机性导致性能评估的不稳定。 -
自助法(Bootstrapping):
采用有放回的随机抽样方式从原始数据集中抽取样本形成训练集,剩余的样本作为测试集。
由于是有放回的抽样,自助法允许同一个样本在训练集中出现多次,或在训练集和测试集中同时出现。
自助法产生的数据集改变了原始数据集的分布,因此在估计模型误差时可能引入偏差。
-
-
分层抽样法的优点:
-
可以保持比例的代表性。
-
使得样本分布更加均匀,提高估计的精度。
-
确保每个类别在样本中都有足够的代表,可以减少抽样的误差。
-
-
随机抽样或分层抽样切割数据集的方法:
train_test_split()。''' 参数说明: - train_data是所要划分的样本特征集 - train_target是所要划分的样本结果 - test_size=[0,1]/int,样本占比,如果是整数的话就是样本的数量,None时默认0.25 - train_size,同上,test_size可替代,None时默认0.75 - random_state=int/None,随机数种子,不同随机数种子划分的结果不同,None时每次种子随机 - shuffle=Bool,如果True则会先将数据打乱顺序然后再进行划分 - stratify=list/None,保持split前类的分布,也就是分层抽样的分层依据,如果想要依据train_target分类,可直接使stratify=train_target,None时随机抽样 ''' # 以下有具体值的为默认值 from sklearn.model_selection import train_test_split x_train,x_test, y_train,y_test = train_test_split(train_data, train_target, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None) -
不用进行随机选取情况:
-
时间序列数据:随机打乱数据会破坏数据的时间依赖性和顺序性。
-
特定顺序的数据:有些数据项之间可能存在特定的逻辑或物理顺序,例如图像中的连续帧。
-
类别分布不平衡的数据:不同类别的样本数量差距可能很大,直接随机选取会导致某些类别样本在数据集中过少或过多。
-
有特定结构的数据:数据可能具有特定的结构或模型,例如社交网络中的图或网络。
-
模型创建
Logistic Regression
-
逻辑回归(Logistic Regression)模型是线性模型的分类模型,不是回归模型,与LinearRegression混淆。
-
Logistic Regression通过建立概率模型,将线性回归的输出结果通过逻辑函数(通常是sigmoid函数)转换为概率形式,从而进行分类预测(解决二分类问题)。
-
创建基于线性模型的分类模型(逻辑回归)的流程:
# 引入LogisticRegression类 from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # 划分数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) # 创建LogisticRegression类的示例(以下为默认参数) logreg = LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, l1_ratio=None, max_iter=100, multi_class='auto', n_jobs=None, penalty='l2', random_state=None, solver='lbfgs', tol=0.0001, verbose=0, warm_start=False) # 拟合模型 logreg.fit(x_train, y_train) # 预测与评估准确度 y_pred = logreg.predict(y_test) accuracy = accuracy_score(y_test, y_pred) logreg.score(x_test, y_test) # 评测数据与标签,y是y_test的教师标签 -
LogisticRegression类的参数说明:
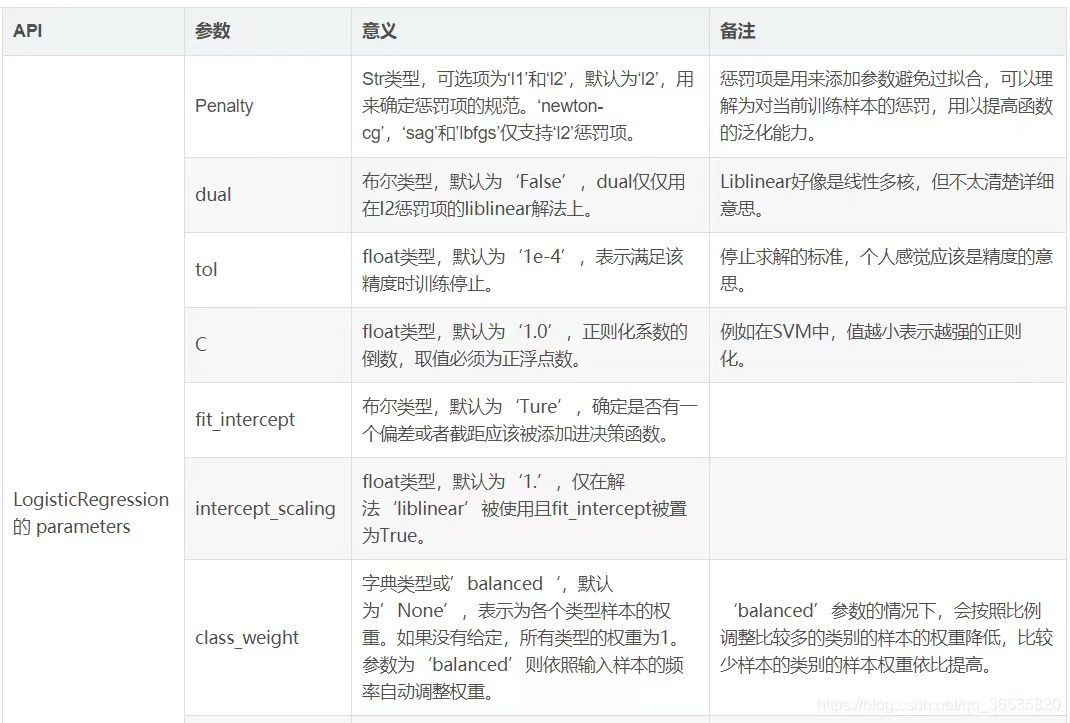
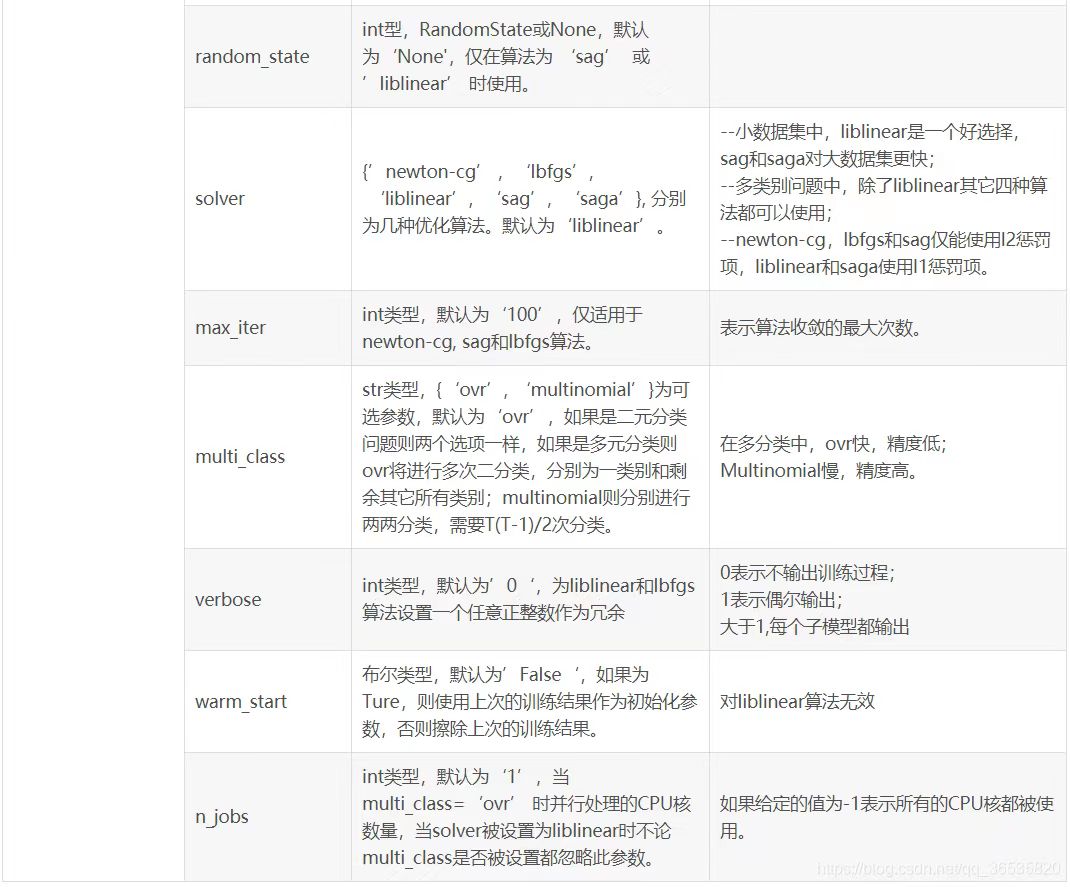
Decision Tree Classifier
-
分类决策树(DecisionTreeClassifier)是一种预测模型,主要用于解决分类问题,是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一个类别,基于这样的结构,根据样本的属性值进行逐步测试,最终将样本划分到某个叶节点,即某个类别中。
-
创建分类决策树的流程:
# 引入DecisionTreeClassifier类 from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score # 划分数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) # 创建DecisionTreeClassifier类的示例(以下为默认参数) clf = DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0, monotonic_cst=None) # 拟合模型 clf.fit(x_train, y_train) # 预测与评估准确度 y_pred = clf.predict(y_test) accuracy = accuracy_score(y_test, y_pred) clf.score(x_test, y_test) # 评测数据与标签,y是y_test的教师标签 -
DecisionTreeClassifier类的参数说明:
参数 类型 描述 criterion可选值为'gini'或'entropy', default='gini' 特征选择标准,默认'gini'即CART算法。 splitter可选值为'best'或'random', default='best' 用于在每个节点选择划分特征的算法。'best'表示在全局选择最优划分,'random'表示随机局部选择最优划分。 max_depthint, default=None 树的最大深度。如果为None,则树会生长到所有叶子都是纯的,或者直到所有叶子包含少于 min_samples_split的样本。min_samples_splitint or float, default=2 拆分内部节点所需的最小样本数。如果是float,则表示的是占训练集样本总数的比例。 min_samples_leafint or float, default=1 一个叶子节点必须具有的最小样本数。如果是float,则它表示的是占训练集样本总数的比例。 min_weight_fraction_leaffloat, default=0.0 最小样本权重和,如果小于则会和兄弟节点一起被剪枝,这个参数用于处理带权重的样本。 max_featuresint, float, string or None, default=None 考虑用于查找最佳划分的特征数量。如果是int,则随机考虑 max_features个特征;如果是float,则max_features是特征总数的比例;如果是'sqrt',则max_features=sqrt(n_features);如果是'log2',则max_features=log2(n_features);如果是None,则max_features=n_features。random_stateint, RandomState instance or None, default=None 控制随机性的参数。对于 splitter='random'时尤为重要。max_leaf_nodesint or None, default=None 最大叶子节点数。如果为None,则不限制叶子节点的数量。 min_impurity_decreasefloat, default=0.0 如果一个分割点导致的不纯度减少小于这个值,则该分割点不会被考虑。 class_weightdict, list of dict or "balanced", default=None 类别权重。如果为None,则所有类别的权重相等。如果为'balanced',则类别权重与类频率成反比。也可以提供一个字典,指定每个类别的权重。 ccp_alphafloat, default=0.0 复杂度参数用于最小成本-复杂度剪枝。增加此参数的值会导致树更早停止生长。 monotonic_cstlist of bools or None, default=None 如果给出,布尔值的列表,其长度等于类的数量,表示是否应该强制决策树为单调的。请注意,单调性仅适用于单变量分割的决策树。
Random Forest Classifier
-
分类随机森林(RandomForestClassifier)是一种集成学习方法,基于构建并结合多个决策树来提高模型的预测性能。随机森林通过随机有放回地抽取数据样本集来训练多个决策树,并且每个决策树在构建过程中也随机抽取特征进行划分。
-
创建分类随机森林的流程:
# 引入RandomForestClassifier类 from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score # 划分数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) # 创建RandomForestClassifier类的示例(以下为默认参数) clf = RandomForestClassifier(n_estimators=100, criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features='sqrt', max_leaf_nodes=None, min_impurity_decrease=0.0, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None, monotonic_cst=None) # 拟合模型 clf.fit(x_train, y_train) # 预测与评估准确度 y_pred = clf.predict(y_test) accuracy = accuracy_score(y_test, y_pred) clf.score(x_test, y_test) # 评测数据与标签,y是y_test的教师标签 -
RandomForestClassifier类的参数说明:
参数名称 参数类型 描述 n_estimatorsint, optional default=100 随机森林里的树木数量。 criterion可选值为"gini" 或 "entropy", str, optional default='gini' 用于测量分裂质量的函数。 max_depthint or None, optional default=None 树的最大深度。如果为 None,则节点将展开直到所有叶子都是纯净的或者直到所有叶子包含少于 min_samples_split的样本。min_samples_splitint or float, optional default=2 分裂内部节点所需的最小样本数。 min_samples_leafint or float, optional default=1 一个叶节点应该具有的最小样本数。 min_weight_fraction_leaffloat, optional default=0.0 在叶子节点所有输入样本权重总和中的最小权重分数。 max_featuresstr, int or None, optional default='sqrt' 寻找最佳分裂时要考虑的特征数量。 max_leaf_nodesint or None, optional default=None 最大叶节点数量。 min_impurity_decreasefloat, optional default=0.0 如果这种分裂导致不纯度的减少大于或等于此值,则节点将被分裂。 bootstrapbool, optional default=True 是否在构建树时使用自助法样本。 oob_scorebool, optional default=False 是否使用袋外样本来估计泛化误差。 n_jobsint or None, optional default=None 用于运行的并行运行的线程数。如果为 -1,则使用所有可用的处理器。 random_stateint, RandomState instance or None, optional default=None 控制随机性的参数。 verboseint, optional default=0 控制建树过程的日志输出的详细程度。 warm_startbool, optional default=False 当设置为 True 时,重用解决方案的上一次调用的解作为初始化,否则,只需擦除之前的解决方案。 class_weightdict, list of dict or "balanced", optional default=None 指定类别的权重。 ccp_alphanon-negative float, optional default=0.0 复杂度参数用来最小化损失函数的正则化项。 max_samplesint or float, optional default=None 如果 bootstrap为 True,则这是从 X 中抽取样本以构建每个基础学习器的样本数。monotonic_cstlist of lists or array-like or None, optional default=None 约束树中的每个特征的单调性。
输出模型预测结果
-
.predict()方法可以输出预测标签。 -
.predict_proba()可以输出标签概率。
predict_proba(X) 方法会返回一个数组,其形状为 (n_samples, n_classes),其中 n_samples 是输入样本的数量,n_classes 是目标变量的类别数。数组的每一个元素 [i, j] 表示第 i 个样本属于第 j 个类别的概率。 -
预测标签的概率可以用来调整阈值、估计不确定性、校准概率、指定调整决策等。
模型评估
模型评估的三种方法
-
模型评估是为了知道模型的泛化能力。
-
机器学习和数据科学中用于评估分类模型性能的三种工具方法:交叉验证、混淆矩阵和ROC曲线。
交叉验证
-
交叉验证(cross-validation)是一种评估泛化性能的统计学方法,它比单次划分训练集和测试集的方法更加稳定、全面,主要用于防止模型过拟合。
-
交叉验证法的常见形式:
-
简单交叉验证(Hold-out Cross-validation):
将数据集分为训练集和测试集两部分。
使用训练集训练模型,并在测试集上评估其性能。
这种方法的优点是简单,但缺点是可能由于数据划分的随机性导致评估结果的不稳定。 -
K折交叉验证(K-fold Cross-validation):
将数据集分成K个大小相等的子集(或尽可能相等)。
每次选择K-1个子集作为训练集,剩下的一个子集作为验证集。
进行K次迭代,每次使用不同的子集作为验证集。
计算K次迭代的平均性能作为模型的最终评估结果。
这种方法的优点是评估结果较为稳定,能够充分利用数据集进行训练和验证。
-
留一交叉验证(Leave-one-out Cross-validation):
当数据集非常小时,可以使用留一交叉验证。
每次选择一个样本作为验证集,其余样本作为训练集。
对于数据集中的每个样本都进行这样的操作,最终计算所有迭代的平均性能。
这种方法的优点是评估结果非常稳定,但由于每次迭代只使用一个样本作为验证集,所以计算成本较高。 -
分层交叉验证(Stratified Cross-validation):
当数据集中各类别的样本数量不平衡时,可以使用分层交叉验证。
在划分数据集时,确保每个子集中各类别的样本比例与原始数据集中的比例相同。
这有助于避免由于类别不平衡导致的评估偏差。 -
时间序列交叉验证(Time-series Cross-validation):
适用于时间序列数据,其中数据的顺序非常重要。
将数据按照时间顺序划分成多个子集,并确保训练集总是在验证集之前。
这种方法有助于评估模型在时间序列预测任务中的性能。
-
-
k-交叉验证的示例:
# 引入cross_val_score函数 from sklearn.model_seleciton import cross_val_score from sklearn.linear_model import LogisticRegression # 划分数据集并处理模型 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) logreg = LogisticRegression() # 10折交叉验证(以下为默认参数) score = cross_val_score(logreg, x_train, y_train, cv=None, groups=None, scoring=None, n_jobs=None, verbose=0, fit_params=None, params=None, pre_dispatch='2*n_jobs', error_score=nan) # k折交叉验证分数 print(f"score:{score}") # 平均交叉验证分数 print("Average cross-validation score: {:.2f}".format(scores.mean())) -
cross_val_score()参数说明:参数 类型 描述 estimatorobject 要进行交叉验证的估计器(模型)对象,必须实现了 fit和predict方法(对于分类问题)或predict_proba方法(对于概率估计)。Xarray-like 输入数据的特征矩阵,形状为 (n_samples, n_features)。yarray-like, optional 目标变量的数组,形状为 (n_samples,)或(n_samples, n_outputs)。groupsarray-like, optional 数组,形状为 (n_samples,),用于将数据集分割成训练集和测试集。如果提供了这个参数,则cv必须是能够处理组信息的交叉验证迭代器,例如GroupKFold或LeaveOneGroupOut。scoringstr, callable, list/tuple, dict or None, optional default=None 用于评估模型性能的评分方法。可以是一个字符串(如 'accuracy'、'f1'、'roc_auc'等,对应于sklearn.metrics中的评分函数),也可以是一个评分函数。如果为None,则默认使用估计器的(以下为默认参数)edKFold`等);还可以是一个可迭代对象,产生训练/测试索引。cvint, cross-validation generator or an iterable, optional default=None 确定交叉验证策略的参数。可以是整数,表示折叠数(如cv=5表示5折交叉验证);也可以是一个交叉验证迭代器(如KFold, StratifiedKFold等);还可以是一个可迭代对象,产生训练/测试索引。 n_jobsint or None, optional default=None 用于并行运行的作业数。如果为 -1,则使用所有可用的处理器。如果为None,则不并行运行。verboseint, optional default=0 控制日志输出的详细程度。 fit_paramsdict, optional default=None 传递给估计器 fit方法的额外参数。paramsdict or None, optional default=None 传递给估计器的参数。如果为 None,则使用估计器的默认参数。pre_dispatchint, str or 'all', optional default='2*n_jobs' 控制并行计算中的作业调度策略。整数表示要预分派的作业数;字符串 'all'表示使用所有可用的处理器。error_score'raise' or numeric, optional default=np.nan 如果在拟合估计器时发生错误,则返回的值。如果设置为 'raise',则会引发错误。如果设置为一个数值,则会用该数值作为分数。 -
不需要显示拟合模型
.fit(),因为在交叉验证中会自动拟合模型。 -
K值越多,意味着每次用于训练和验证的数据子集越小,同时验证的次数也越多,当k折越多时的影响:
-
模型评估的稳定性增加
-
计算量增加
-
过拟合风险减小
-
超参数选择更精确
-
混淆矩阵
-
混淆矩阵(Confusion Matrix)也被称为误差矩阵,是一种特定的表格,用来呈现算法性能的可视化效果,通常用于监督学习(非监督学习,通常叫做聚类)。混淆矩阵的每一列代表了预测类别,每一行代表了数据的真实归属类别。主要用于模型的精度评估,不仅可以判断分类器的好坏,还可以做一些性能评估,比如敏感度、特异度、准确率和召回率等。
-
混淆矩阵的四个基本元素:
- 真正例(True Positive, TP):实际为正例,且被分类器划分为正例的样本数。
- 假正例(False Positive, FP):实际为负例,但被分类器划分为正例的样本数。
- 假负例(False Negative, FN):实际为正例,但被分类器划分为负例的样本数。
- 真负例(True Negative, TN):实际为负例,且被分类器划分为负例的样本数。
-
准确率(Accuracy)、精确率(Precision)、召回率(Recall)和F-分数(F-score)是分类任务中常用的评估指标,它们可以帮助我们全面评估分类模型的性能。
-
准确率:
准确率是指模型正确分类的样本数与总样本数之比。\(Accuracy = \dfrac{TP + TN}{TP + FP + FN + TN}\)
准确率越高,说明模型预测正确的比例越大。
-
精确率:
精确率是指模型预测为正例的样本中真正为正例的比例。\(Precision = \dfrac{TP}{TP + FP}\)
精确率越高,说明模型预测为正样本的实例中,错误预测的比例越低。
-
召回率
召回率是指实际为正例的样本中被模型正确识别为正例的比例。\(Recall = \dfrac{TP}{TP + FN}\)
召回率越高,说明模型能够找到更多的正样本,减少漏报的情况。
-
f-分数
F-分数是准确率和召回率的调和平均值,用于综合评估模型的性能。$F-score = \dfrac{2 * precision * recall}{precision + recall} $
F-分数越高,说明模型在精确率和召回率之间达到了较好的平衡。
-
-
二分类问题的混淆矩阵(Confusion Matrix for Binary Classification)是一个2x2的表格,用于展示二分类问题中分类器对正样本(Positive)和负样本(Negative)的预测结果与实际标签之间的对比。
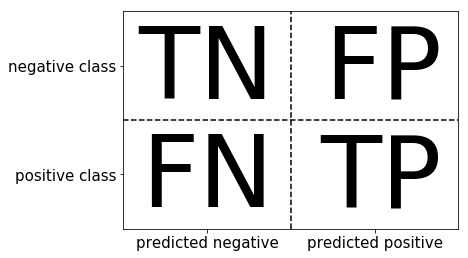
-
二分类混淆矩阵的使用示例:
# 引入confusion_matrix类 from sklearn.metrics import confusion_matrix from sklearn.linear_model import LogisticRegression # 划分数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) # 创建LogisticRegression类的示例 logreg = LogisticRegression() # 拟合模型并预测 logreg.fit(x_train, y_train) y_pred = logreg.predict(x_test) # 混淆矩阵计算与结果输出 cm = confusion_matrix(y_pred, y_test, labels=None, sample_weight=None, normalize=None) print(f"confusion-matrix:{cm}") TP = cm[0][0] # 真正例 FP = cm[0][1] # 假正例 FN = cm[1][0] # 假负例 TN = cm[1][1] # 真负例 accuracy = (TP + TN) / (TP + FP + FN + TN) precision = TP / (TP + FP) recall = TP / (TP + FN) f1_score = 2 * (precision * recall) / (precision + recall) print(f"准确率: {accuracy:.2f}") print(f"精确率: {precision:.2f}") print(f"召回率: {recall:.2f}") print(f"F1分数: {f1_score:.2f}") -
confusion_matrix()参数说明:参数名称 类型 说明 y_truearray-like of shape (n_samples,) 真实的目标值。 y_predarray-like of shape (n_samples,) 预测的目标值。 labelsarray-like of shape (n_classes) default=None 用于索引混淆矩阵的标签列表。这可以用来指定标签的顺序,或者包括在 y_true或y_pred中未出现的标签。sample_weightarray-like of shape (n_samples,) default=None 样本权重。 normalize{'true', 'pred', 'all'} default=None 归一化方式。如果true,则返回的混淆矩阵的行将被归一化,以显示每个标签的真正例率。如果pred,则返回的混淆矩阵的列将被归一化,以显示每个标签的预测正例率。如果all,则返回的混淆矩阵的行和列都将被归一化。如果None,则返回的混淆矩阵将不会进行归一化。
ROC曲线
-
ROC曲线,全称接收者操作特征曲线(Receiver Operating Characteristic),是一种用于评估分类模型性能的工具。它以假阳性率(False Positive Rate,FPR)为横轴,真阳性率(True Positive Rate,TPR)为纵轴。在ROC曲线图像中,对角线代表随机猜测模型的预测表现。ROC曲线越靠近左上角,分类模型的性能越好。通过比较ROC曲线下方的面积,即AUC值(Area Under Curve),可以确定模型的准确性。
-
ROC曲线的意义:
-
模型性能的全局评估:ROC曲线提供了一个全局的视角来评估模型的性能,而不仅仅是依赖于单个阈值下的评估指标。通过查看曲线在不同阈值下的表现,可以全面了解模型在不同分类边界下的性能。
-
模型性能的可视化:ROC曲线将模型的性能以图形化的方式展示出来,使得评估结果更加直观易懂。通过比较不同模型的ROC曲线,可以清晰地看出哪个模型在整体上具有更好的性能。
-
模型间的比较:在多个模型之间进行比较时,ROC曲线可以作为一个统一的度量标准。通过计算曲线下面积(AUC值),可以对不同模型的性能进行定量比较,从而选择出最优的模型。
-
处理不平衡数据集:在处理不平衡数据集时,ROC曲线和AUC值通常比准确率等其他指标更加稳健。这是因为ROC曲线关注的是模型在正负样本上的分类性能,而不是整体的正确率,因此对于正负样本比例差异较大的情况,ROC曲线能够提供更准确的性能评估。
-
-
ROC曲线的使用示例:
# 引入roc_curve类 from sklearn.metrics import roc_curve, auc from sklearn.linear_model import LogisticRegression # 划分数据集 x_train, x_test, y_train, y_test = train_test_split(x, y, stratify=y) # 创建LogisticRegression类的示例 logreg = LogisticRegression() # 拟合模型并预测获取概率 logreg.fit(x_train, y_train) y_score = logreg.decision_function(x_test) # 计算ROC曲线 fpr, tpr, thresholds = roc_curve(y_test, y_score, pos_label=None, sample_weight=None, drop_intermediate=True) # 计算AUC值 roc_auc = metrics.auc(fpr, tpr) # 绘制ROC曲线 plt.plot(fpr, tpr, label="ROC Curve") plt.xlabel("FPR") plt.ylabel("TPR (recall)") plt.legend(loc=4) -
roc_curve()函数参数说明:参数名称 类型 说明 y_truearray-like, shape = (n_samples,) 真实的标签,通常是二分类的0和1。 y_scorearray-like, shape = (n_samples,) 模型为每个样本预测的正类概率或决策函数值。 pos_labelstr or int, default=None 正类的标签。如果 None,则正类将被假定为1(尽管在二分类中y_true通常只包含0和1)。sample_weightarray-like of shape (n_samples,), optional 样本权重。 drop_intermediatebool, optional default=True 是否删除一些不会导致阈值更改的中间阈值,这将导致ROC曲线更少折点,从而更平滑。默认为 True。 -
在进行多类别的ROC曲线计算中两两一组并选择其中一个为正类 对每个类别进行ROC计算。



