[BZOJ4987] Tree

[BZOJ4987] Tree

题目大意:从前有棵树,找出\(K\)个结点\(A_1, A_2, A_3,\cdots A_k\),使\(\sum\limits_{1 \leq i \leq K-1}{} dis(A_i,A_{i+1})\)

Solution

先画一个样例图

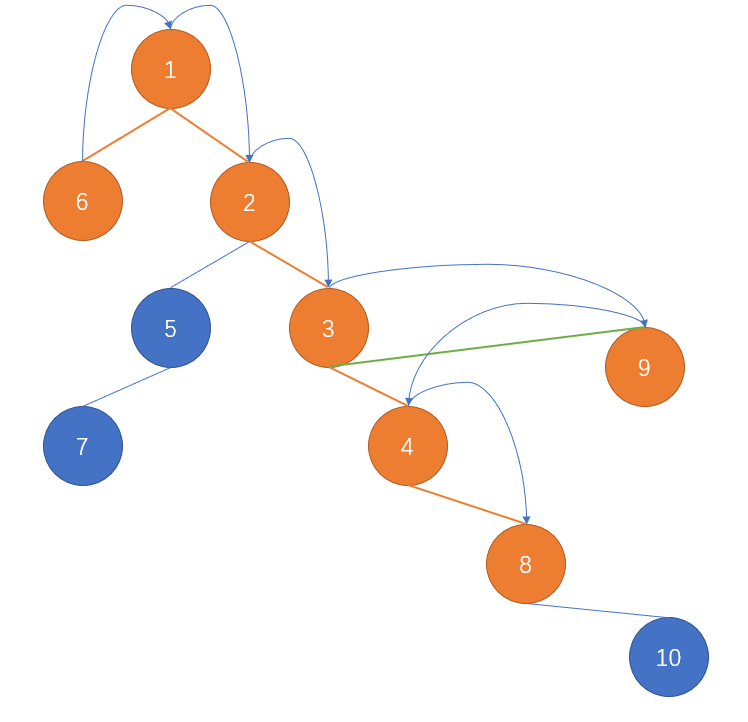
延伸出两个结论

1. 选出的点集一定是一个联通树; 因为如果不连通,即点集在树上有不相邻的,那么完全可以选两个不相邻的点中间的点进入点集,一定更优

2. 和最小的情况下,有一条链只经过一遍,剩余的边要经历两次; 这个配合样例图,画一画就可以

• 状态:\(f[i][j][k]\)表示以\(i\)为根节点且\(i\)必须选,在他的子树里面取\(j\)条边,有\(k\)个子节点是链的端点的最小花费

复杂度:相当于在\(i​\)为根的子树中枚举点对\((u,v)​\),且两者不在一个子树中,所以只有当找到\(lca(v,u)​\)才能找到点对\((u,v)​\),所以时间复杂度为\(O(n^2)​\)

Code

#include <bits/stdc++.h>

using namespace std;

const int N = 3000 + 10;

int n, k, ecnt, ans = 2147483647;
int head[N], siz[N];
int f[N][N][4];

struct Edge {
	int to, next, val;
}e[N << 1];

inline void adde(int x, int y, int z) {
	e[++ecnt].to = y;
	e[ecnt].next = head[x];
	e[ecnt].val = z;
	head[x] = ecnt;
}

void dfs(int x, int fa) {
	siz[x] = 1;
	f[x][0][0] = f[x][0][1] = 0;//没选边,没有端点或此结点作为一条链的端点,那么花费为0
	for(int i = head[x]; i; i = e[i].next) {
		if(e[i].to == fa) continue;
		dfs(e[i].to, x);
		for(int j = siz[x] - 1; j >= 0; --j)//选的边最多都是size - 1,下文j+k+1也是说明选的边最多都是size - 1
			for(int k = siz[e[i].to] - 1; k >= 0; --k)
				for(int l = 2; l >= 0; --l)//枚举此结点的端点数
					for(int m = l; m >= 0; --m)//2 - (m & 1) 是如果两或零个端点都在这个子节点的话, 那么当前结点到此子节点的这段路是不包含在主链里的,要乘二 
						f[x][j + k + 1][l] = min(f[x][j + k + 1][l], f[e[i].to][k][m] + f[x][j][l - m] + e[i].val * (2 - (m & 1))); 
		siz[x] += siz[e[i].to];//在最后加上子节点的size是因为,多叉树,两个两个合并 
	}
}

int main() {
	scanf("%d %d", &n, &k);
	for(int i = 1, la, lb, lc; i <= n - 1; ++i) {
		scanf("%d %d %d", &la, &lb, &lc);
		adde(la, lb, lc);
		adde(lb, la, lc);
	}
	memset(f, 0x3f, sizeof(f));//初始化
	dfs(1, 0);
	for(int i = 1; i <= n; ++i)
		for(int j = 0; j <= 2; ++j)
			ans = min(ans, f[i][k - 1][j]);
	printf("%d", ans);
	return 0;
}