[BZOJ4237] 稻草人

[BZOJ4237] 稻草人

题目大意:给出一个平面坐标系,\(n\)个点\((x_i,y_i)\),求以任一个点为左下角,另一个点为右上角,最多能组成多少个矩形中没有其他点的矩形.(\(x_i\)互不相同,\(y_i\)互不相同)

Solution

将区间二分后分别处理,并将两个区间共同组成的答案统计.

1. 按照\(x\)从小到大对整个区间排序

2. 将区间分为\([l,mid]\)和\([mid+1, r]\),先求解\([l,mid]\)

3. 两段区间分别按照\(y\)从大到小排序

   得到\((2,2), (0,0)\)和\((3,4),(4,3)\)

4. 建立两个单调栈,\(lsta\)的\(x\)单调递减,\(rsta\)的\(x\)单调递增,先加入左边的元素,来统计有多少的右边元素可以构成矩形

   

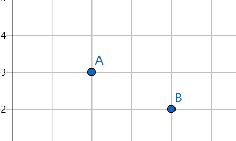
5. 在左栈里面,\(A\)先加入的,如果\(B\)加入后\(x\)还变大了,说明\(A\)根本不会影响到\(B\)

   

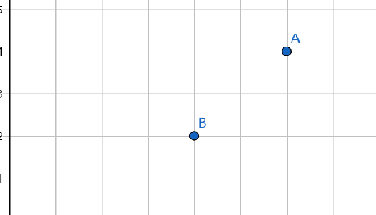
6. 在右栈里,\(A\)先加入,如果\(B\)加入后\(x\)还变小了,说明\(A\)根本就没有用了,统计不到答案了

7. 统计完答案后,用\(x\)排序,消除影响,处理\([mid+1,r]\)

Code

#include <iostream>
#include <cstdio>
#include <algorithm>
    
using std::sort;
    
const int N = 2e5 + 10;
    
struct  Node{
    int x, y;
}a[N], l_sta[N], r_sta[N];
    
int n;
long long ans;
    
inline int read(){
    int x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}
    
inline bool cmp1(Node a, Node b){
    return a.x < b.x;
}
    
inline bool cmp2(Node a, Node b){
    return a.y > b.y;
}
    
inline int find(int x, int qwq){
    int l = 1, r = qwq, mid;
    while(l <= r){
        mid = l + ((r - l) >> 1);
        if(r_sta[mid].y <= x){
            r = mid - 1;
        }
        else {
            l = mid + 1;
        }
    }
    return r;
}
    
void solve(int l, int r){
    if(l >= r) return;
    int mid = l + ((r - l) >> 1);
    solve(l, mid);
    sort(a + l, a + mid + 1, cmp2);
    sort(a + mid + 1, a + r + 1, cmp2);
    int r_top = 0, l_top = 0, p = mid + 1, ll, rr;
    l_sta[0].y = r_sta[0].y = 2100000000;
    for(int i = l; i <= mid; ++i){//l写成1也是醉了
        while(p <= r && a[p].y > a[i].y){
            while(r_top && a[p].x < r_sta[r_top].x){
                r_top--;
            }
            r_sta[++r_top] = a[p];
            p++;
        }
        while(l_top && a[i].x > l_sta[l_top].x){
            l_top--;
        }
        l_sta[++l_top] = a[i];
        ll = find(l_sta[l_top - 1].y, r_top) + 1;
        rr = find(l_sta[l_top].y, r_top);
        if(rr >= ll)
            ans += (long long)(rr - ll + 1);
         
    }
    sort(a + l, a + mid + 1, cmp1);
    sort(a + mid + 1, a + r + 1, cmp1);
    solve(mid + 1, r);
}
    
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n ;++i){
        scanf("%d %d", &a[i].x, &a[i].y);
    }
    sort(a + 1, a + n + 1, cmp1);
    solve(1, n);
    printf("%lld\n", ans);
    return 0;
}