HihoCoder 后缀数组入门1-4 题解
#1403 : 后缀数组一·重复旋律
后缀数组做法:
后缀数组中Height[i]代表着后缀i跟后缀i-1的LCP(最长公共前缀),也就是出现次数至少为2次的最长子串。
而要求出现次数最少为K次的最长子串,即求Height[i]数组中所有长度为K-1的区间中的最小值的最大值。
用后缀数组处理出Height数组之后,那就有好几种方法处理了,这里使用单调队列。

#include<bits/stdc++.h> using namespace std; const int N=2e4+11; int a[N]; int sa[N],ra[N],height[N]; int cntr[N],tsa[N]; //cntr"桶",tsa[i]临时数组,不同情况意义不同 deque<int> q; //根据第一关键字ra[i]和以及按第二关键字[i+l]排好序的tsa进行基数排序 void sasort(int n,int m){ for(int i=0;i<=m;i++) cntr[i]=0; for(int i=1;i<=n;i++) cntr[ra[i]]++; for(int i=1;i<=m;i++) cntr[i]+=cntr[i-1]; for(int i=n;i>=1;i--) sa[cntr[ra[tsa[i]]]--]=tsa[i]; } void getsa(int n){ int m=100;//初始的数据大小,比如ascii码的话,一般为127 for(int i=1;i<=n;i++) ra[i]=a[i],tsa[i]=i; sasort(n,m); for(int l=1;l<=n;l<<=1){ int num=0; //[n-l+1,n]的数第二关键字为0,按第二关键字排序肯定是在前面 for(int i=n-l+1;i<=n;i++) tsa[++num]=i; // 如果sa[i]>l,那么它可以作为sa[i]-l的第二关键字 for(int i=1;i<=n;i++) if(sa[i]>l) tsa[++num]=sa[i]-l; sasort(n,m); //重复空间利用,用tsa暂时存下上一轮的ra用于比较求出新的ra memcpy(tsa,ra,(n+1)*sizeof(int)); ra[sa[1]]=1; for(int i=2;i<=n;i++){ ra[sa[i]]=ra[sa[i-1]]; if(tsa[sa[i]]!=tsa[sa[i-1]]||tsa[sa[i]+l]!=tsa[sa[i-1]+l]) ra[sa[i]]++; } m=ra[sa[n]]; if(m>=n) break; } for(int i=1,j=0;i<=n;i++){ if(j) j--; while(a[i+j]==a[sa[ra[i]-1]+j]) j++; height[ra[i]]=j; } return ; } int solve(int n,int k){ while(!q.empty()) q.pop_back(); for(int i=1;i<k;i++){ while(!q.empty()&&height[i]<=height[q.back()]) q.pop_back(); q.push_back(i); } int ans=0; for(int i=k;i<=n;i++){ while(!q.empty()&&i-q.front()>=k-1) q.pop_front(); while(!q.empty()&&height[i]<=height[q.back()]) q.pop_back(); q.push_back(i); ans=max(ans,height[q.front()]); } return ans; } int main(){ int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); a[n+1]=-1; getsa(n); printf("%d\n",solve(n,k)); return 0; }
因为我是先学的后缀自动机,在学的后缀数组,所有对前三题我也尝试了后缀自动机的做法。
后缀自动机中,endpos[i]为i状态中子串出现的次数,而len[i]为i状态的最长子串长度。具体求法在后缀自动机中再介绍。
处理出endpos和len之后,我们就统计下每个出现次数的最长子串长度,然后k~n找最大值即可。

#include<bits/stdc++.h> using namespace std; const int N=4e4+11; struct Sam{ int size,last,len[N],link[N],trans[N][111]; int endpos[N]; Sam(){ size=last=1; memset(trans,0,sizeof(trans)); } void extend(int x){ int cur=++size,u; endpos[cur]=1; len[cur]=len[last]+1; for(u=last;u&&!trans[u][x];u=link[u]) trans[u][x]=cur; if(!u) link[cur]=1; else{ int v=trans[u][x]; if(len[v]==len[u]+1) link[cur]=v; else{ int clone=++size; len[clone]=len[u]+1; link[clone]=link[v]; memcpy(trans[clone],trans[v],sizeof(trans[v])); for(;u&&trans[u][x]==v;u=link[u]) trans[u][x]=clone; link[cur]=link[v]=clone; } } last=cur; } }A; int a[N],ans[N]; vector<int> vv[N]; void dfs(int u){ int lenv=vv[u].size(); for(int i=0;i<lenv;i++){ int v=vv[u][i]; dfs(v); A.endpos[u]+=A.endpos[v]; } } void solve(){ for(int i=1;i<=A.size;i++) vv[A.link[i]].push_back(i); dfs(1); for(int i=1;i<=A.size;i++) ans[A.endpos[i]]=max(ans[A.endpos[i]],A.len[i]); } int main(){ int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) A.extend(a[i]); solve(); int res=0; for(int i=k;i<=n;i++) res=max(res,ans[i]); printf("%d\n",res); return 0; }
#1407 : 后缀数组二·重复旋律2
后缀数组做法:
跟上题类似,但这次要找的是不重叠的子串。而如果存在某个长度的子串符合条件,那么比它的子串肯定也符合条件。
所以这个长度存在一个单调性,那么我们可以二分子串的长度,然后去判断这个长度合不合理。
假设当前二分的答案为x,对于存不存在至少出现两次长度为x的子串,直接便是看存不存在height[i]>=x。怎么判断存在不重复的呢。
我们把连续的height[i]>=x,对应的后缀分在同一组,这样就保证了该组中所有后缀两两之间的最长公共前缀都是不小于k的。注意,是连续的。
然后我们找出这一组中最大的sa,和最小的sa,即后缀在原串中相应的位置。而如果max{sa}-min{sa}大于等于x的话,就说明存在长度至少为x且不重叠的子串。
也就是至少min{sa}到min{sa}+x这一段,和max{sa}到max{sa}+x的这一段是相同的,而max{sa}-min{sa}>=x,这两段并不存在重叠部分。

#include<bits/stdc++.h> using namespace std; const int N=2e5+11; int a[N]; int sa[N],ra[N],height[N]; int cntr[N],tsa[N]; void sasort(int n,int m){ for(int i=0;i<=m;i++) cntr[i]=0; for(int i=1;i<=n;i++) cntr[ra[i]]++; for(int i=1;i<=m;i++) cntr[i]+=cntr[i-1]; for(int i=n;i>=1;i--) sa[cntr[ra[tsa[i]]]--]=tsa[i]; } void getsa(int n){ int m=1000; for(int i=1;i<=n;i++) ra[i]=a[i],tsa[i]=i; sasort(n,m); for(int l=1;l<=n;l<<=1){ int num=0; for(int i=n-l+1;i<=n;i++) tsa[++num]=i; for(int i=1;i<=n;i++) if(sa[i]>l) tsa[++num]=sa[i]-l; sasort(n,m); swap(ra,tsa); ra[sa[1]]=1; for(int i=2;i<=n;i++){ ra[sa[i]]=ra[sa[i-1]]; if(tsa[sa[i]]!=tsa[sa[i-1]]||tsa[sa[i]+l]!=tsa[sa[i-1]+l]) ra[sa[i]]++; } m=ra[sa[n]]; if(m>=n) break; } for(int i=1,j=0;i<=n;i++){ if(j) j--; while(a[i+j]==a[sa[ra[i]-1]+j]) j++; height[ra[i]]=j; } return ; } bool check(int n,int k){ int maxsa,minsa; for(int i=1;i<=n;i++){ if(height[i]<k){ maxsa=sa[i]; minsa=sa[i]; }else{ maxsa=max(maxsa,sa[i]); minsa=min(minsa,sa[i]); if(maxsa-minsa>=k) return true; } }//将连续的height大于k归为一组判断,如果遇到中断的则重置 return false; } int solve(int n){ int l=1,r=n,mid,ans=0; while(l<=r){ mid=(l+r)>>1; if(check(n,mid)) ans=mid,l=mid+1; else r=mid-1; } return ans; } int main(){ int n,k; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); getsa(n); printf("%d\n",solve(n)); return 0; }
后缀自动机做法:
在类似求endpos[i],我们同时可以求出maxpos[i],minpos[i],即每个状态的endpos集合中的最大值和最小值。
endpos[i]自然就是这个状态下子串的出现次数了,那么判断最长不重叠部分,在len[i]以及maxpos[i]-minpos[i]+1中取个最小值即可。

如上图,存在两种情况,绿色部分就是不重叠部分的最长长度。
但这题不能用后缀自动机做,会超内存,可能是我不会优化吧,啊,so vegetable,所以代码就随便看看就好了。
扩展一下,如果是至少出现不重复的子串的个数的话,后缀自动机就得用遍历所有长度,此时是n方的复杂度。
而后缀自动机的话,直接用不重叠部分的最长长度,减去该状态中最短子串长度即可。

#include<bits/stdc++.h> using namespace std; const int N=1e5+11,inf=0x3f3f3f3f; struct Sam{ int size,last,len[N],link[N],trans[N][1011]; int endpos[N],minpos[N],maxpos[N]; Sam(){ size=last=1; memset(trans,0,sizeof(trans)); } void extend(int pos,int x){ int cur=++size,u; endpos[cur]=1; len[cur]=len[last]+1; minpos[cur]=maxpos[cur]=pos; for(u=last;u&&!trans[u][x];u=link[u]) trans[u][x]=cur; if(!u) link[cur]=1; else{ int v=trans[u][x]; if(len[v]==len[u]+1) link[cur]=v; else{ int clone=++size; len[clone]=len[u]+1; minpos[cur]=inf;maxpos[cur]=-1; link[clone]=link[v]; memcpy(trans[clone],trans[v],sizeof(trans[v])); for(;u&&trans[u][x]==v;u=link[u]) trans[u][x]=clone; link[cur]=link[v]=clone; } } last=cur; } }A; int a[N],ans[N]; vector<int> vv[N]; void dfs(int u){ int lenv=vv[u].size(); for(int i=0;i<lenv;i++){ int v=vv[u][i]; dfs(v); A.endpos[u]+=A.endpos[v]; A.minpos[u]=min(A.minpos[u],A.minpos[v]); A.maxpos[u]=max(A.maxpos[u],A.maxpos[v]); } } int solve(){ for(int i=1;i<=A.size;i++) vv[A.link[i]].push_back(i); dfs(1); int ans=0; for(int i=1;i<=A.size;i++) ans=max(ans,min(A.len[i],A.maxpos[i]-A.minpos[i]+1)); // 出现两次以上,不重叠的子串个数 // int dis=A.maxpos[i]-A.minpos[i]; // int mi=min(dis,A.len[i]); // int milen=A.len[i]-A.len[A.link[i]]+1; // ans+=max(0,mi-milen+1); return ans; } int main(){ int n; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) A.extend(i,a[i]); printf("%d\n",solve()); return 0; }
#1415 : 后缀数组三·重复旋律3
后缀数组做法:
我们将第二个字符串接在第一个字符串后面,并且两者中间用一个数据中不会出现的字符(比如说#)分隔开。
此时求出排名相邻的不在同一个字符串的height中的最大值即可。
因为如果两个后缀在不同串中,计算它们最长前缀时必定要跨越过那些相邻height值。

#include<bits/stdc++.h> using namespace std; const int N=2e5+11; char s1[N],s2[N]; int a[N]; int sa[N],ra[N],height[N]; int cntr[N],tsa[N]; void sasort(int n,int m){ for(int i=0;i<=m;i++) cntr[i]=0; for(int i=1;i<=n;i++) cntr[ra[i]]++; for(int i=1;i<=m;i++) cntr[i]+=cntr[i-1]; for(int i=n;i>=1;i--) sa[cntr[ra[tsa[i]]]--]=tsa[i]; } void getsa(int n){ int m=132; for(int i=1;i<=n;i++) ra[i]=a[i],tsa[i]=i; sasort(n,m); for(int l=1;l<=n;l<<=1){ int num=0; for(int i=n-l+1;i<=n;i++) tsa[++num]=i; for(int i=1;i<=n;i++) if(sa[i]>l) tsa[++num]=sa[i]-l; sasort(n,m); swap(ra,tsa); ra[sa[1]]=1; for(int i=2;i<=n;i++){ ra[sa[i]]=ra[sa[i-1]]; if(tsa[sa[i]]!=tsa[sa[i-1]]||tsa[sa[i]+l]!=tsa[sa[i-1]+l]) ra[sa[i]]++; } m=ra[sa[n]]; if(m>=n) break; } for(int i=1,j=0;i<=n;i++){ if(j) j--; while(a[i+j]==a[sa[ra[i]-1]+j]) j++; height[ra[i]]=j; } return ; } int main(){ scanf("%s%s",s1+1,s2+1); int lens1=strlen(s1+1),lens2=strlen(s2+1); for(int i=1;i<=lens1;i++) a[i]=s1[i]; a[lens1+1]+='#'; for(int i=1;i<=lens2;i++) a[lens1+1+i]=s2[i]; getsa(lens1+lens2+1); int ans=0; for(int i=1;i<=lens1+lens2+1;i++){ if((sa[i]<=lens1&&sa[i-1]>lens1)||(sa[i]>lens1&&sa[i-1]<=lens1)) ans=max(ans,height[i]); } printf("%d\n",ans); return 0; }
后缀自动机做法:
在后缀自动机部分里会涉及到,这里就不重复了。

#include<bits/stdc++.h> using namespace std; const int N=5e5+11; struct Sam{ int size,last,len[N],link[N],trans[N][31]; Sam(){ size=last=1; } void extend(int x){ int cur=++size,u; len[cur]=len[last]+1; for(u=last;u&&!trans[u][x];u=link[u]) trans[u][x]=cur; if(!u) link[cur]=1; else{ int v=trans[u][x]; if(len[v]==len[u]+1) link[cur]=v; else{ int clone=++size; len[clone]=len[u]+1; link[clone]=link[v]; memcpy(trans[clone],trans[v],sizeof(trans[v])); for(;u&&trans[u][x]==v;u=link[u]) trans[u][x]=clone; link[cur]=link[v]=clone; } } last=cur; } }A; char s[N]; int main(){ scanf("%s",s); int lens=strlen(s); for(int i=0;i<lens;i++) A.extend(s[i]-'a'); scanf("%s",s); lens=strlen(s); int u=1,lcs=0,ans=0,x; for(int i=0;i<lens;i++){ x=s[i]-'a'; while(u!=1&&!A.trans[u][x]) u=A.link[u],lcs=A.len[u]; if(A.trans[u][x]) lcs++,u=A.trans[u][x]; else u=1,lcs=0; // printf("%d %d\n",i,lcs); ans=max(ans,lcs); } printf("%d\n",ans); return 0; }
#1419 : 后缀数组四·重复旋律4
这题只能后缀数组来做,(对于我来说)。
我们可以通过枚举循环串长度,然后再枚举起始位置来得到k,假设当前枚举的长度为l,位置为i,那么k=lcp(i,i+l)/l+1
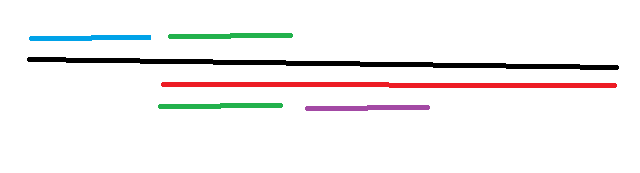
如长图,蓝色部分即为l,i后缀(上面的),跟i+l后缀(下面的)比较的话,一开始当然是蓝色的跟绿色的这段比较
如果他们相等,接下来就是绿色的跟紫色的比较,(注意,他们应该是连续的,只是为了好看,没画连续,虽然也不好看。)
求出他们最长相等的长度,而这一段都是一开始蓝色那部分在循环,所以再除去循环串的长度+1就是答案了。
但很明显,这样的复杂度是n方,我们需要优化一下,也就是不用枚举每个起始位置,只枚举是l倍数的位置。
HihoCoder讲得很好 ,直接搬过来了,侵删。。。。。。。。。。
小Ho:道理是这么个道理。不过如果最优串的开始位置不在l的倍数上呢?
小Hi:即使不是,问题也会太糟糕,假如说最优串位置在x,可以想象我们会枚举到x之后的一个最近位置p,p是l的倍数。并且我们计算出了Suffix(p)和Suffix(p+l)的LCP,lcp(l, p)那么此时的k(l, p)=lcp(l, p)/l+1。
小Hi:对于被我们略过的k(l, p-1), k(l, p-2) ... k(l, p-l+1),它们的上限是k(l, p)+1。
小Ho:没错。因为它们的起始位置距离p不超过l,所以最多比Suffix(p)增加一个循环节。
小Hi:其次,如果k(l, p-1), k(l, p-2) ... k(l, p-l+1)中有一个的值是k(l, p)+1的话,那么k(l, p - l + lcp(l, p) mod l)一定等于k(l, p)+1。(mod是取余运算)
小HO:为什么呢?
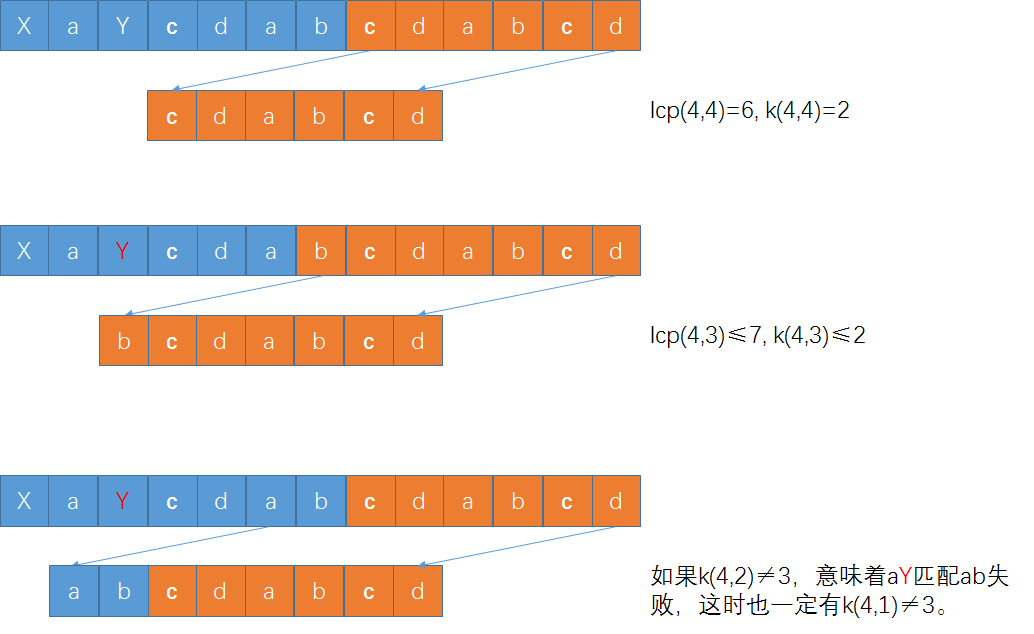
小Hi:举个例子,比如串XaYcdabcdabcd(XY各代表一个不确定的字符,具体代表的字符会影响最后答案,我们后面会分析到),当我们考虑l=4的时候,第一次枚举p=4的起始位置,会求出cdabcdabcd和cdabcd的lcp(4, 4)=6,k(4, 4)=2。根据上面的论断,只有当k(l, p - l + lcp(l, p) mod l)=k(4, 4 - 4 + 6 mod 4)=k(4, 2)=3时,k(4, 1), k(4, 2)和k(4, 3)中才会有3。首先我们可以判断k(4, 3)一定不可能等于3,因为无论Y是哪个字符,Ycdabcdabcd和bcdabcd的LCP即lcp(4, 3)最大是7,不到8。 其次如果k(4, 2) ≠ 3,那么k(4, 1)也没戏。因为如果k(4, 2) ≠ 3,说明aY和ab匹配不上,这时无论X是哪个字符,XaY和dab匹配不上,lcp(4, 1) < l,k(4, 1) = 1。
小Ho:哦,我有点明白了。k(l, p - l + lcp(l, p) mod l)是一个分界线,右边的值因为LCP不够大,一定不能增加一个循环节。并且如果k(l, p - l + lcp(l, p) mod l)没有增加循环节的话,说明[p - l + lcp(l, p) mod l, p]这段中间匹配出错,左边的lcp也跟着雪崩,更不可能增加循环节了。
所以现在的复杂度就是n/1+n/2+n/3+...1,经典求极限,也就是nlogn,(准确的好像是nlnn)
哦,最后一点,查询lcp(i,i+l)也就是RMQ问题嘛,懒得建线段树,这里用ST算法实现。

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=3e5+11; 4 char a[N]; 5 int lg2[N],st[N][21]; 6 int sa[N],ra[N],height[N]; 7 int cntr[N],tsa[N]; 8 void sasort(int n,int m){ 9 for(int i=0;i<=m;i++) cntr[i]=0; 10 for(int i=1;i<=n;i++) cntr[ra[i]]++; 11 for(int i=1;i<=m;i++) cntr[i]+=cntr[i-1]; 12 for(int i=n;i>=1;i--) sa[cntr[ra[tsa[i]]]--]=tsa[i]; 13 } 14 void getsa(int n){ 15 int m=127; 16 for(int i=1;i<=n;i++) ra[i]=a[i],tsa[i]=i; 17 sasort(n,m); 18 for(int l=1;l<=n;l<<=1){ 19 int num=0; 20 for(int i=n-l+1;i<=n;i++) tsa[++num]=i; 21 for(int i=1;i<=n;i++) if(sa[i]>l) tsa[++num]=sa[i]-l; 22 sasort(n,m); 23 swap(ra,tsa); 24 ra[sa[1]]=1; 25 for(int i=2;i<=n;i++){ 26 ra[sa[i]]=ra[sa[i-1]]; 27 if(tsa[sa[i]]!=tsa[sa[i-1]]||tsa[sa[i]+l]!=tsa[sa[i-1]+l]) ra[sa[i]]++; 28 } 29 m=ra[sa[n]]; 30 if(m>=n) break; 31 } 32 for(int i=1,j=0;i<=n;i++){ 33 if(j) j--; 34 while(a[i+j]==a[sa[ra[i]-1]+j]) j++; 35 height[ra[i]]=j; 36 } 37 return ; 38 } 39 void getst(int n){ 40 lg2[1]=0; 41 for(int i=2;i<=n;i++) lg2[i]=lg2[i/2]+1; 42 for(int i=1;i<=n;i++) st[i][0]=height[i]; 43 for(int j=1;j<=lg2[n];j++){ 44 for(int i=1;i+(1<<j)-1<=n;i++) 45 st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]); 46 } 47 } 48 int getlcp(int l,int r){ 49 l=ra[l];r=ra[r]; 50 if(l>r) swap(l,r); 51 l++; 52 int k=lg2[r-l+1]; 53 return min(st[l][k],st[r-(1<<k)+1][k]); 54 } 55 int solve(int n){ 56 getst(n); 57 int ans=0; 58 for(int l=1;l<=n;l++){ 59 for(int i=1;i+l<=n;i+=l){ 60 int r=getlcp(i,i+l); 61 ans=max(ans,r/l+1); 62 if(i>l-r%l){ 63 ans=max(ans,getlcp(i-l+r%l,i+r%l)/l+1); 64 } 65 } 66 } 67 return ans; 68 } 69 int main(){ 70 while(~scanf("%s",a+1)){ 71 int lena=strlen(a+1); 72 getsa(lena); 73 printf("%d\n",solve(lena)); 74 } 75 return 0; 76 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号