HDU3551 &2020牛客暑期多校训练营（第一场）1 or 2

题目链接HDU3551

啊，没想到有一天会再次遇到带花树的题。之前写过带花树的博客，但不看板子真敲不出来。

具体的带花树板子就不重复了，这里只研究建图思路。思路来源hdu 3551（一般图的匹配）

题目大意是：给你一个图，问能不能删去一些边，使得所有i点的度数都等于d[i]。

如果d[i]都等于1的话，这次就赤裸裸的一般图最大匹配了嘛。而现在d[i]不为1，所以我们要进行拆点。

将每个点的度数都重新拆成一个点，而每条边对于的端点也进行拆点重新编号，并与它们每个度数的点相先。

如样例

4 4

1 2

3 4

2 3

1 4

1

2

1

0

则拆出下图

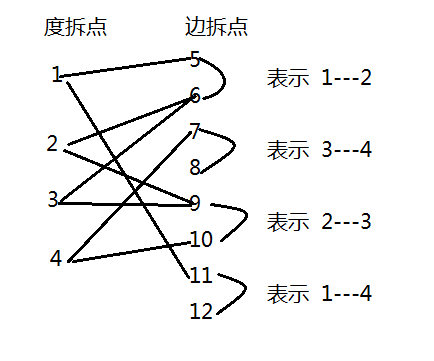
当我们求出这个图的最大匹配时，对于完美的匹配自然是一边是度拆点，而一边是边拆点。而两个端点都是边拆点的则是要删去的边。

如1-5 2-6实际上便是1的一个度数点与2的一个度数点相连，也对应着原边中1--2这条边。而11-12的话，代表着这条边可以删去，对应这原图中的1--4这条边。

#include<bits/stdc++.h>
using namespace std;
const int N=2011,M=20011;
struct Side{
    int v,ne;
}S[M<<1];
queue<int> q;
int uu[N],vv[N],d[N],id[N][N];
int sn,fn,head[N],pp[N],col[N],pre[N],fa[N],vis[N];
void init(){
    sn=fn=0;
    memset(pp,0,sizeof(pp));
    memset(vis,0,sizeof(vis));
    memset(head,-1,sizeof(head));
}
void add(int u,int v){
    S[sn].v=v;
    S[sn].ne=head[u];
    head[u]=sn++;
}
void add2(int u,int v){
    add(u,v);add(v,u);
} 
int find(int x){
    return fa[x]==x ? x : fa[x]=find(fa[x]);
}
int flca(int x,int y){
    ++fn;
    x=find(x),y=find(y);
    while(vis[x]!=fn){
        vis[x]=fn;
        x=find(pre[pp[x]]);
        if(y){
            int temp=x;x=y;y=temp;
        }
    }
    return x;
}
void blossom(int x,int y,int fl){
    while(find(x)!=fl){
        pre[x]=y;
        y=pp[x];
        if(col[y]==2){
            col[y]=1;
            q.push(y);
        }
        if(find(x)==x) fa[x]=fl;
        if(find(y)==y) fa[y]=fl;
        x=pre[y];
    }
}
int aug(int u,int n){
    for(int i=0;i<=n;i++){
        fa[i]=i;
        pre[i]=0;
        col[i]=0;
    }
    while(!q.empty()) q.pop();
    q.push(u);
    col[u]=1;
    while(!q.empty()){
        u=q.front();
        q.pop();
        for(int i=head[u],v;~i;i=S[i].ne){
            v=S[i].v;
            if(find(u)==find(v)||col[v]==2) continue;
            if(!col[v]){
                pre[v]=u;col[v]=2;
                if(!pp[v]){
                    for(int x=v,y;x;x=y){    
                        y=pp[pre[x]];
                        pp[x]=pre[x];
                        pp[pre[x]]=x;
                    }
                    return 1; 
                }
                col[pp[v]]=1;q.push(pp[v]);
            }else{
                int fl=flca(u,v);
                blossom(u,v,fl);
                blossom(v,u,fl);
            }
        }
    }
    return 0;
}
bool solve(int n,int m){
    init();
    int idn=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=d[i];j++) id[i][j]=++idn;
    for(int i=0;i<m;i++){
        for(int j=1;j<=d[uu[i]];j++) add2(id[uu[i]][j],idn+1);
        for(int j=1;j<=d[vv[i]];j++) add2(id[vv[i]][j],idn+2);
        add2(idn+1,idn+2);
        idn+=2;
    }
    for(int i=1;i<=idn;i++) if(!pp[i]) aug(i,idn);
    for(int i=1;i<=idn;i++) if(!pp[i]) return false;
    return true;
}
int main(){
    int n,m,u,v,t=1,T;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        for(int i=0;i<m;i++) scanf("%d%d",&uu[i],&vv[i]);
        for(int i=1;i<=n;i++) scanf("%d",&d[i]);
        printf("Case %d: %s\n",t++,solve(n,m) ? "YES" : "NO");
    }
    return 0;
}

至于牛客多校的那题，自然则是这题的简化版，d[i]只有1,2,改一下数据的读入顺序即可。