区间异或和的和
Sum of xor sum
这两题是一样的,但后面那个数据为空的,你输出“下次一定”都能过。
我们要求的就是给你任意区间[L,R],能得出这么一个东西

,直接从数的本身下手,是没有想法的。异或这个位操作有关的,我们可以从二进制位来考虑,如果我们知道了每一位对答案的贡献,那么最后直接把所有位的答案再加起来即可。
这里我们对j位进行讨论,用sum[i-1][j]来表示,前i-1个数在二进制位置j的答案前缀和,当在加多一个数a[i],怎么得到sum[i][j]呢?
首先,当加多a[i]之后,多的区间自然是[1,i],[2,i]...[3,i]以i为右边界的区间,这时我们再看哪些区间对答案有贡献。
用xr[i][j]表示前i个数在j位置的异或和,那对答案有贡献的区间情况无非两种,设区间为[k,i],便是xr[k][j]=0,xr[i][j]=1跟xr[k][j]=1,xr[i][j]=1。
因为xr[k][j]跟xr[i][j]相同的话,不就表示着j位在(k,i]区间内有偶数个1,这偶数个1异或为0,那(k,i]也就是[k+1,i]区间对答案自然没有贡献。
由此我们可知,当xr[i][j]=1时,对答案有贡献的区间左端点k便是xr[k][j]=0,而xr[i][j]=0时则相反。
所以这时候我们要用cnt0[i][j],来记录前i个数在j位置的异或和为0的数有多少个,cnt1[i][j]同理。明显初始值,cnt0[0][j]=1,cnt1[0][j]=0。
那么sum[i][j]=sum[i-1][j]+2j*(xr[i][j] ? cnt0[i-1][j] : cnt1[i-1][j]); (2j为j为的权重),也就是在[0,i-1]中找一个左端点k,使得(k,i]中有奇数个1。
要求区间[L,R]内的答案,自然是对每一位求ans+=sum[R]-sum[L-1],j位区间右端点在[L,R]范围中的答案
但此时还多算了点答案,也就是左端点在[0,L-1],而右端点在[L,R]中的答案,所以还得把这部分减去
ans-=2j*cnt0[L-2][j]*(cnt1[R][j]-cnt1[L-1][j]),ans-=2j*cnt1[L-2][j]*(cnt0[R][j]-cnt0[L-1][j])
为什么是L-2呢,看在[0,i-1]中找一个左端点k,使得(k,i]中有奇数个1那里,我们的区间是左开右闭的。
如果是L-1的话,就变成了(L-1,L~R]=[L,L~R]多减去了左端点为L的情况。

#include<bits/stdc++.h> using namespace std; const int N=1e5+11,M=21,md=1000000007; int cf2[N],sum[N][M],xr[N][M],cnt[3][N][M]; int main(){ int t,n,q,x; cf2[0]=1; for(int i=0;i<M;i++){ if(i) cf2[i]=cf2[i-1]<<1; cnt[0][0][i]=1; cnt[1][0][i]=0; } scanf("%d",&t); while(t--){ scanf("%d%d",&n,&q); for(int i=1;i<=n;i++){ scanf("%d",&x); for(int j=0;j<M;j++){ int pw=(x>>j)&1; pw=xr[i][j]=xr[i-1][j]^pw; cnt[0][i][j]=cnt[0][i-1][j]+(pw^1); cnt[1][i][j]=cnt[1][i-1][j]+pw; sum[i][j]=sum[i-1][j]+1ll*cf2[j]*cnt[pw^1][i-1][j]%md; if(sum[i][j]>=md) sum[i][j]-=md; } } int l,r; while(q--){ scanf("%d%d",&l,&r); long long ans=0; for(int i=0;i<M;i++){ ans+=sum[r][i]-sum[l-1][i]; ans=(ans%md+md)%md; if(l>=2){ ans-=1ll*cf2[i]*cnt[0][l-2][i]%md*(cnt[1][r][i]-cnt[1][l-1][i])%md; ans=(ans%md+md)%md; ans-=1ll*cf2[i]*cnt[1][l-2][i]%md*(cnt[0][r][i]-cnt[0][l-1][i])%md; ans=(ans%md+md)%md; } } printf("%lld\n",ans); } } return 0; }
那很明显,上面的做法并不支持修改,所以要是还有单点修改的话,我们就得用线段树来处理。(见的世面太小,区间修改的题还没见过)
我们要维护哪些东西呢,len为这个区间的长度,sum[j]为这个区间内j位的答案,lj[j]是以这个区间的左部来作为区间的左端点使得区间内有奇数个1的右端点个数
而rj[j]自然是以这个区间的右部来作为区间的右端点使得区间内有奇数个1的左端点个数,cnt[j]就是记录这个区间内有几个1。
其他地方就跟正常线段树差不多,主要就是补充说明一下向上更新时,两个区间的合并。
Tree merge(Tree &ll,Tree &rr){ Tree ans; ans.l=ll.l;ans.r=rr.r; for(int i=0;i<M;i++){ ans.sum[i]=ll.sum[i]+rr.sum[i]; ans.sum[i]+=ll.rj[i]*(rr.len-rr.lj[i]); ans.sum[i]+=rr.lj[i]*(ll.len-ll.rj[i]);
if(ll.cnt[i]&1) ans.lj[i]=ll.lj[i]+(rr.len-rr.lj[i]); else ans.lj[i]=ll.lj[i]+rr.lj[i]; if(rr.cnt[i]&1) ans.rj[i]=rr.rj[i]+(ll.len-ll.rj[i]); else ans.rj[i]=rr.rj[i]+ll.rj[i]; ans.cnt[i]=ll.cnt[i]+rr.cnt[i]; ans.len=ll.len+rr.len; } return ans; }
直接用代码进行说明(这里当然也可以不传引用直接传值,但传引用会快一点),假设要合并的是ll,rr区间,其中ll区间合并时是在左边的,而rr是右边的,而合并后的区间是ans
除了之前两区间的答案之和,合并之后就得多考虑左端点在ll中,右端点在rr中的区间对答案的贡献,也就是考虑左边奇数个1,右边偶数个1还有反过来的情况。
代码也就是ans.sum[i]+=ll.rj[i]*(rr.len-rr.lj[i]) ans.sum[i]+=rr.lj[i]*(ll.len-ll.rj[i]);
因为rr是接在ll的右边,所以ans的lj[i],就得看ll的1的数目来决定。而ans的rj[j]同理即可,这里就对lj[i]进行说明。
如果ll总共有奇数个1,那么跟rr中应该以左部为左端点的区间就应该要求有偶数个1,也就是拿区间的长度减去奇数个1的情况来得到。
代码就是if(ll.cnt[i]&1) ans.lj[i]=ll.lj[i]+(rr.len-rr.lj[i]); //左边奇数个1,右边以左部为左端点的区间就应该有偶数个1
else ans.lj[i]=ll.lj[i]+rr.lj[i];//相反右边以左部为左端点的区间就应该有奇数个1

#include<bits/stdc++.h> #define L(x) (x<<1) #define R(x) (x<<1|1) #define M(x) ((T[x].l+T[x].r)>>1) using namespace std; const int N=1e5+11,M=20,md=1000000007; typedef long long ll; struct Tree{ int l,r,len; int sum[M],lj[M],rj[M],cnt[M]; Tree(){ for(int i=0;i<M;i++) sum[i]=lj[i]=rj[i]=cnt[i]=0; } }T[N<<2]; int a[N]; Tree merge(Tree &ll,Tree &rr){ Tree ans; ans.l=ll.l;ans.r=rr.r; for(int i=0;i<M;i++){ ans.sum[i]=ll.sum[i]+rr.sum[i]; ans.sum[i]+=1ll*ll.rj[i]*(rr.len-rr.lj[i])%md; if(ans.sum[i]>=md) ans.sum[i]-=md; ans.sum[i]+=1ll*rr.lj[i]*(ll.len-ll.rj[i])%md; if(ans.sum[i]>=md) ans.sum[i]-=md; if(ll.cnt[i]&1) ans.lj[i]=ll.lj[i]+(rr.len-rr.lj[i]); else ans.lj[i]=ll.lj[i]+rr.lj[i]; if(rr.cnt[i]&1) ans.rj[i]=rr.rj[i]+(ll.len-ll.rj[i]); else ans.rj[i]=rr.rj[i]+ll.rj[i]; ans.cnt[i]=ll.cnt[i]+rr.cnt[i]; ans.len=ll.len+rr.len; } return ans; } void build(int x,int l,int r){ T[x].l=l;T[x].r=r; if(l==r){ T[x].len=1; for(int i=0;i<M;i++){ T[x].sum[i]=T[x].lj[i]=T[x].rj[i]=T[x].cnt[i]=((a[l]>>i)&1); } return ; } build(L(x),l,M(x)); build(R(x),M(x)+1,r); T[x]=merge(T[L(x)],T[R(x)]); return ; } Tree query(int x,int l,int r){ if(l<=T[x].l&&r>=T[x].r) return T[x]; if(r<=M(x)) return query(L(x),l,r); else if(l>M(x)) return query(R(x),l,r); else{ Tree ll=query(L(x),l,r),rr=query(R(x),l,r); return merge(ll,rr); } } int main(){ int t,n,q; scanf("%d",&t); while(t--){ scanf("%d%d",&n,&q); for(int i=1;i<=n;i++) scanf("%d",&a[i]); build(1,1,n); int l,r,res; while(q--){ scanf("%d%d",&l,&r); Tree ans=query(1,l,r); res=0; for(int i=M-1;i>=0;i--) res=(2ll*res%md+ans.sum[i])%md; printf("%lld\n",res); } } return 0; }
牛客异或Tree
lt是一个三维生物,他掌管着二维世界的运行规律,某一天他发现一颗有nnn个节点的无根树,该树只有点权,没有边权,现在他要进行mmm次操作,每次进行以下两种操作之一:
1.选择一个节点,将其点权进行修改。
2.给出参数u,v,询问u->v的简单路径上的所有点按顺序组成一个数组,计算这个数组的牛逼值。
牛逼值就是区间异或和的和。
这题涉及到树链剖分,不会的,可以右上角点击关闭了。
虽然设有树链剖分的专栏,但一直没更,而且之前图论的博客也很粗糙,有空得进行更新,下次一定。
(大胆妖孽,我一眼就看出你是一只鸽子精。)
这题的话,无非就是的先用树链剖分处理一下,然后线段树中要增加个单点修改。也就是两部分的模板套起来即可。
但需要注意的就是在树链剖分的树链的查询,答案的合并问题。
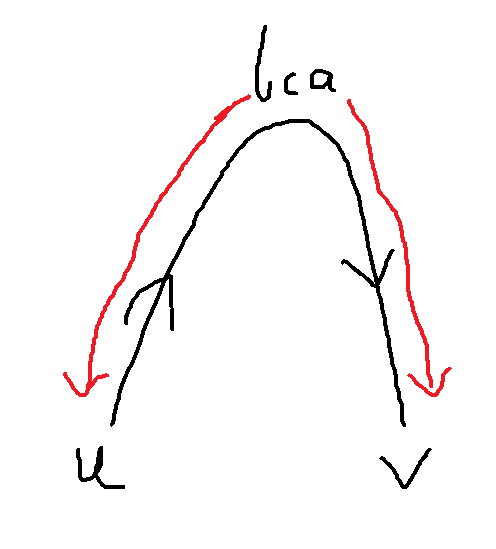
我们要求u到v中的答案,可以看成u->lca,和lca->v这两条链(两个区间)合并的答案。
而在树链上,我们每次查一段区间内的答案,所得到的答案的方向是红线方向。
所以对于u->lca这条链上的答案就得把方向反过来之后再合并,而反过来其实就是lj[i]跟rj[i]进行互换即可。
这需要分别保存两题链上的答案,最后再把它们合并。
那么对于每次在u->lca链上,每新增加一部分答案,就得把那个答案方向反过来,再作为右边的区间与原先的合并。
而对于lca->v链上的就是,新答案作为左区间跟原先的合并。

#include<bits/stdc++.h> #define L(x) (x<<1) #define R(x) (x<<1|1) #define M(x) ((T[x].l+T[x].r)>>1) using namespace std; typedef long long ll; const int N=5e4+11,M=31; typedef long long ll; struct Tree{ int l,r,len; int sum[M],lj[M],rj[M],cnt[M]; Tree(){ l=r=len=0; for(int i=0;i<M;i++) sum[i]=lj[i]=rj[i]=cnt[i]=0; } }T[N<<2]; int a[N],b[N]; Tree merge(Tree &ll,Tree &rr){ Tree ans; ans.l=ll.l;ans.r=rr.r; for(int i=0;i<M;i++){ ans.sum[i]=ll.sum[i]+rr.sum[i]; ans.sum[i]+=ll.rj[i]*(rr.len-rr.lj[i]); ans.sum[i]+=rr.lj[i]*(ll.len-ll.rj[i]); if(ll.cnt[i]&1) ans.lj[i]=ll.lj[i]+(rr.len-rr.lj[i]); else ans.lj[i]=ll.lj[i]+rr.lj[i]; if(rr.cnt[i]&1) ans.rj[i]=rr.rj[i]+(ll.len-ll.rj[i]); else ans.rj[i]=rr.rj[i]+ll.rj[i]; ans.cnt[i]=ll.cnt[i]+rr.cnt[i]; } ans.len=ll.len+rr.len; return ans; } void build(int x,int l,int r){ T[x].l=l;T[x].r=r; if(l==r){ T[x].len=1; for(int i=0;i<M;i++){ T[x].sum[i]=T[x].lj[i]=T[x].rj[i]=T[x].cnt[i]=((b[l]>>i)&1); } return ; } build(L(x),l,M(x)); build(R(x),M(x)+1,r); T[x]=merge(T[L(x)],T[R(x)]); return ; } void updata(int x,int pos,int val){ if(T[x].l==pos&&T[x].r==pos){ for(int i=0;i<M;i++){ T[x].sum[i]=T[x].lj[i]=T[x].rj[i]=T[x].cnt[i]=((val>>i)&1); } return ; } if(pos<=M(x)) updata(L(x),pos,val); else updata(R(x),pos,val); T[x]=merge(T[L(x)],T[R(x)]); return ; } Tree query(int x,int l,int r){ if(l<=T[x].l&&r>=T[x].r) return T[x]; if(r<=M(x)) return query(L(x),l,r); else if(l>M(x)) return query(R(x),l,r); else{ Tree ll=query(L(x),l,r),rr=query(R(x),l,r); return merge(ll,rr); } } //上面为线段树维护区间异或和的和 struct Side{ int v,ne; }S[N<<1]; char op[18]; int sn,head[N],tn,tid[N],size[N],dep[N]; int top[N],fa[N],son[N]; void initS(int n){ sn=tn=0; for(int i=0;i<=n;i++){ fa[i]=son[i]=0; size[i]=1; dep[i]=1; head[i]=-1; } } void addS(int u,int v){ S[sn].v=v; S[sn].ne=head[u]; head[u]=sn++; } void dfs1(int u){ for(int i=head[u];~i;i=S[i].ne){ int v=S[i].v; if(v==fa[u]) continue; fa[v]=u; dep[v]=dep[u]+1; dfs1(v); size[u]+=size[v]; if(size[v]>=size[son[u]]) son[u]=v; } } void dfs2(int u,int tf){ tid[u]=++tn; b[tn]=a[u]; top[u]=tf; if(!son[u]) return ; dfs2(son[u],tf); for(int i=head[u];i!=-1;i=S[i].ne){ int v=S[i].v; if(v!=fa[u]&&v!=son[u]) dfs2(v,v); } } Tree querypath(int x,int y){ int flag=1; Tree ans1,ans2,temp; while(top[x]!=top[y]){ if(dep[top[x]]<dep[top[y]]){ flag^=1; swap(x,y); } temp=query(1,tid[top[x]],tid[x]); if(flag){ for(int i=0;i<M;i++) swap(temp.lj[i],temp.rj[i]); ans1=merge(ans1,temp); }else ans2=merge(temp,ans2); x=fa[top[x]]; } flag^=1; if(dep[x]>dep[y]){ swap(x,y); flag^=1; } temp=query(1,tid[x],tid[y]); if(flag){ for(int i=0;i<M;i++) swap(temp.lj[i],temp.rj[i]); ans1=merge(ans1,temp); }else ans2=merge(temp,ans2); ans1=merge(ans1,ans2); return ans1; } int main(){ int t,n,m,op,u,v; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); initS(n); for(int i=1;i<n;i++){ scanf("%d%d",&u,&v); addS(u,v); addS(v,u); } dfs1(1); dfs2(1,1); build(1,1,n); while(m--){ scanf("%d%d%d",&op,&u,&v); if(op==1) updata(1,tid[u],v); else{ Tree ans=querypath(u,v); ll res=0; for(int i=M-1;i>=0;i--) res=((res<<1ll)+ans.sum[i]); printf("%lld\n",res); } } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号