图论之一般图相关内容
什么是一般图?很一般的图就是一般图,没有什么特殊的定义。
二分图的话,可以求一个最大匹配,一般图同样也可以,引入一下最大匹配的概念。
在一个无向图中,定义一条边覆盖的点为这条边的两个端点。找到一个边集S包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。
简单的来说就是,找出图中最多数量的边,这些边互不相交。
一般图的最大匹配这个概念是在一次中石油OJ的一次签到时听说的,当时以为那题可以用网络流做,但怎么建图都建不出来,然后又觉得可以用二分图的最大匹配来解决,但怎么搞也搞不出来,我真是太vegetable了。
回到正题,一般图的最大匹配,是由带花树算法来解决,所谓“花”就是有带奇数边的环,树就是交错树,交错树就是,从未匹配点r寻找匹配点,则以r作为树根,由增广路径延伸出来形成交错树(因为是匹配边-非匹配边互相交错)。
这里就来简单说一说带花树算法的具体实现,但有些细节,我自己也不是很明白,所以无法讲清楚,大概就过一遍算法流程。
先放上大佬博客镇一镇。
BAJim_H的【学习小记】一般图最大匹配——带花树算法
风一样的Liz的利用带花树算法解决一般图的最大匹配
litble的如何用带花树算法做一般图匹配
首先的话,先来知道为什么一般图的最大匹配,不能用二分图的最大匹配来做。这是个废话,因为二分图没有奇环,而一般图有奇环。
奇环的导致后果就是奇偶性不确定,也可以说染色不确定,也就当我们以一个点去寻找增广路时,所走的方向不同导致节点的染色也不同。也就匹配乱套了。
像A-B-C-A 就是个奇环,A进行增广的话,A先往B走,A0,B1,C0,A先往C走,A0,C1,B0 不同的方向,BC的奇偶性就不同了。
那二分匹配的话,假设A先匹配B,然后C匹配时,发现A已经匹配了,然后看B能不能换一个匹配,发现可以换成C,然后B匹配C,C匹配A,这就乱套了。
但我们可以把这个奇环缩成一个点,因为奇环里的某个点与外部相连的话,那大可让它与外部的点匹配,然后剩下的偶数个点就可以相互匹配了。
所以带花树算法的核心思想就是把奇环缩点,但因为奇环不只一个,还有可能当前缩的某些点是之前缩过的一些环,那我们找增广路和反回去修改时,是要走过这些环的,这是把点展开就是相当于开花。。。
感觉写得乱乱的,模板题直接来走流程把。
第一步:遍历所有还未匹配的点,把它染成黑色,由黑点去找增广路。
第二步: 当目前找增广路的节点u找到一个节点v了,那就分5种情况处理,
(1)如果v在当前交错树的染色是白色,说明是一个偶环,不用处理。
(2)如果v的染色是黑色了,那么看u和v是否已经在一个奇环里了,在的话,不用处理。
(3)v的染色是黑色,u和v目前不在一个奇环里,很好,开始缩点。
(4)v没有染色,把v染成白色,然后看v之前已经有匹配了吗,没有找到一条增广路,进行增广。
(5)v没有染色,但之前有匹配了,那把它匹配的那个点染成黑色,并去找增广路。
第三步:具体细节看代码注释,没了。
总时间复杂度趋于n3与n4之间,来做几道题耍一耍
模板题

#include<cstdio> #include<queue> using namespace std; const int N=511,M=2e5+11; struct Side{ int v,ne; }S[M<<1]; queue<int> q; int n,sn,fn,head[N],pp[N],col[N],pre[N],fa[N],vis[N]; //pp[i] i节点匹配的节点,pp[i]-i就是匹配边 //col[i] i节点在当前交错树的染色,用于判断奇环 //pre[i] 记录交错树中i的前一个节点 i-pre[i]就是非匹配边 //fa[i] i节点当前交错树花的lca,用于缩点,和判断奇环 //vis用来判断在找lca时,某个点是否走过了 void init(){ sn=fn=0; for(int i=0;i<=n;i++){ pp[i]=0; vis[i]=0; head[i]=-1; } } void add(int u,int v){ S[sn].v=v; S[sn].ne=head[u]; head[u]=sn++; } int find(int x){ return fa[x]==x ? x : fa[x]=find(fa[x]); } int flca(int x,int y){ ++fn; x=find(x),y=find(y); //两个节点匹配边-非匹配边交替往前找,遇到已经走到过的点,那就是花的lca了 while(vis[x]!=fn){ vis[x]=fn; x=find(pre[pp[x]]); if(y){ int temp=x;x=y;y=temp; } } return x; } void blossom(int x,int y,int fl){ //因为开花时奇环可以双向走,因此pre边也要变成双向的。 while(find(x)!=fl){ pre[x]=y;//x是原本的黑点,y是原本的白点,原先已经有pre[y]=x y=pp[x]; if(col[y]==2){//原来是白的,变成黑的了,继续增广 col[y]=1; q.push(y); } //因为有些点可能已经缩在某朵花里了,所以只对还映射自己的点缩点 if(find(x)==x) fa[x]=fl; if(find(y)==y) fa[y]=fl; x=pre[y];//和上面的y=pp[x]就实现匹配边-非匹配边交替走 } } int aug(int u){ for(int i=0;i<=n;i++){ fa[i]=i; pre[i]=0; col[i]=0; }//fa pre col都是相对当前的交错树而言,所以每次都要清空 while(!q.empty()) q.pop(); q.push(u); col[u]=1; while(!q.empty()){ u=q.front(); q.pop(); for(int i=head[u],v;~i;i=S[i].ne){ v=S[i].v; if(find(u)==find(v)||col[v]==2) continue; if(!col[v]){ pre[v]=u;col[v]=2; if(!pp[v]){ for(int x=v,y;x;x=y){ y=pp[pre[x]]; pp[x]=pre[x]; pp[pre[x]]=x; }//非匹配边-匹配边,返回去修改 return 1; } col[pp[v]]=1;q.push(pp[v]); }else{//发现奇环,进行开花(缩点) int fl=flca(u,v); blossom(u,v,fl); blossom(v,u,fl); } } } return 0; } int main(){ int m,u,v; while(~scanf("%d%d",&n,&m)){ init(); while(m--){ scanf("%d%d",&u,&v); add(u,v); add(v,u); } int ans=0; for(int i=1;i<=n;i++) if(!pp[i]) ans+=aug(i); printf("%d\n",ans); for(int i=1;i<=n;i++) printf("%d%c",pp[i]," \n"[i==n]); } return 0; }
题意:给n个石子,先手先任意取一个,然后交替取,但后一个取的石子跟前一个取的石子的曼哈顿距离不能超过L,最后不能取石子的为输,两人地中海聪明,问后手能不能赢。
感觉就很像一道博弈题,真没往一般图最大匹配上想,也是由题解才知道的。
首先我们把石子看成点,它们的距离看成边,这时就可以得到一个或多个连通块,然后当先手在某个连通块先取走一个石子时,接下来就只能在这个连通块中进行选择了。
那么如果我们把这个连通块的石子进行匹配,那么如果有石子没法匹配的话,因为是连通的,匹配边-非匹配边交错,那么取到这个石子的人,肯定就是先手的,先手取掉这个石子后,后手便无法再去取任何石子,这是先手败。
相反如果所有石子都匹配完全,那么不管先手怎么取石子,后手都有一个与之匹配的石子能取,此时便是后手必胜。
而在整个图来看的话,就是得所有的连通块都是完全匹配的,因为每个连通块都是相对独立的,所以就是求整个图是不是完全匹配。

#include<cstdio> #include<queue> #include<cstdlib> using namespace std; const int N=511,M=2e5+11; struct Side{ int v,ne; }S[M<<1]; queue<int> q; int n,sn,fn,head[N],pp[N],col[N],pre[N],fa[N],vis[N]; int x[N],y[N]; void init(){ sn=fn=0; for(int i=0;i<=n;i++){ pp[i]=0; vis[i]=0; head[i]=-1; } } void add(int u,int v){ S[sn].v=v; S[sn].ne=head[u]; head[u]=sn++; } int find(int x){ return fa[x]==x ? x : fa[x]=find(fa[x]); } int flca(int x,int y){ ++fn; x=find(x),y=find(y); while(vis[x]!=fn){ vis[x]=fn; x=find(pre[pp[x]]); if(y){ int temp=x;x=y;y=temp; } } return x; } void blossom(int x,int y,int fl){ while(find(x)!=fl){ pre[x]=y; y=pp[x]; if(col[y]==2){ col[y]=1; q.push(y); } if(find(x)==x) fa[x]=fl; if(find(y)==y) fa[y]=fl; x=pre[y]; } } int aug(int u){ for(int i=0;i<=n;i++){ fa[i]=i; pre[i]=0; col[i]=0; } while(!q.empty()) q.pop(); q.push(u); col[u]=1; while(!q.empty()){ u=q.front(); q.pop(); for(int i=head[u],v;~i;i=S[i].ne){ v=S[i].v; if(find(u)==find(v)||col[v]==2) continue; if(!col[v]){ pre[v]=u;col[v]=2; if(!pp[v]){ for(int x=v,y;x;x=y){ y=pp[pre[x]]; pp[x]=pre[x]; pp[pre[x]]=x; } return 1; } col[pp[v]]=1;q.push(pp[v]); }else{ int fl=flca(u,v); blossom(u,v,fl); blossom(v,u,fl); } } } return 0; } int main(){ int m; while(~scanf("%d",&n,&m)){ init(); for(int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]); scanf("%d",&m); for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(abs(x[j]-x[i])+abs(y[j]-y[i])<=m){ add(i,j); add(j,i); } int ans=0; for(int i=1;i<=n;i++) if(!pp[i]) ans+=aug(i); ans*=2; if(ans==n) puts("YES"); else puts("NO"); } return 0; }
这题便是在中石油见到的那题,是2018-2019 ICPC, NEERC, Northern Eurasia Finals的B题。
题意:每个骑士得同时跟两位女士跳舞(哇,金色渣男),给出每个骑士愿意和哪些女士跳舞,问最多有多少组1男2女这样的组合。
网络流搞不了,二分图搞不了,自己是啥思路也没有,直接上题解。
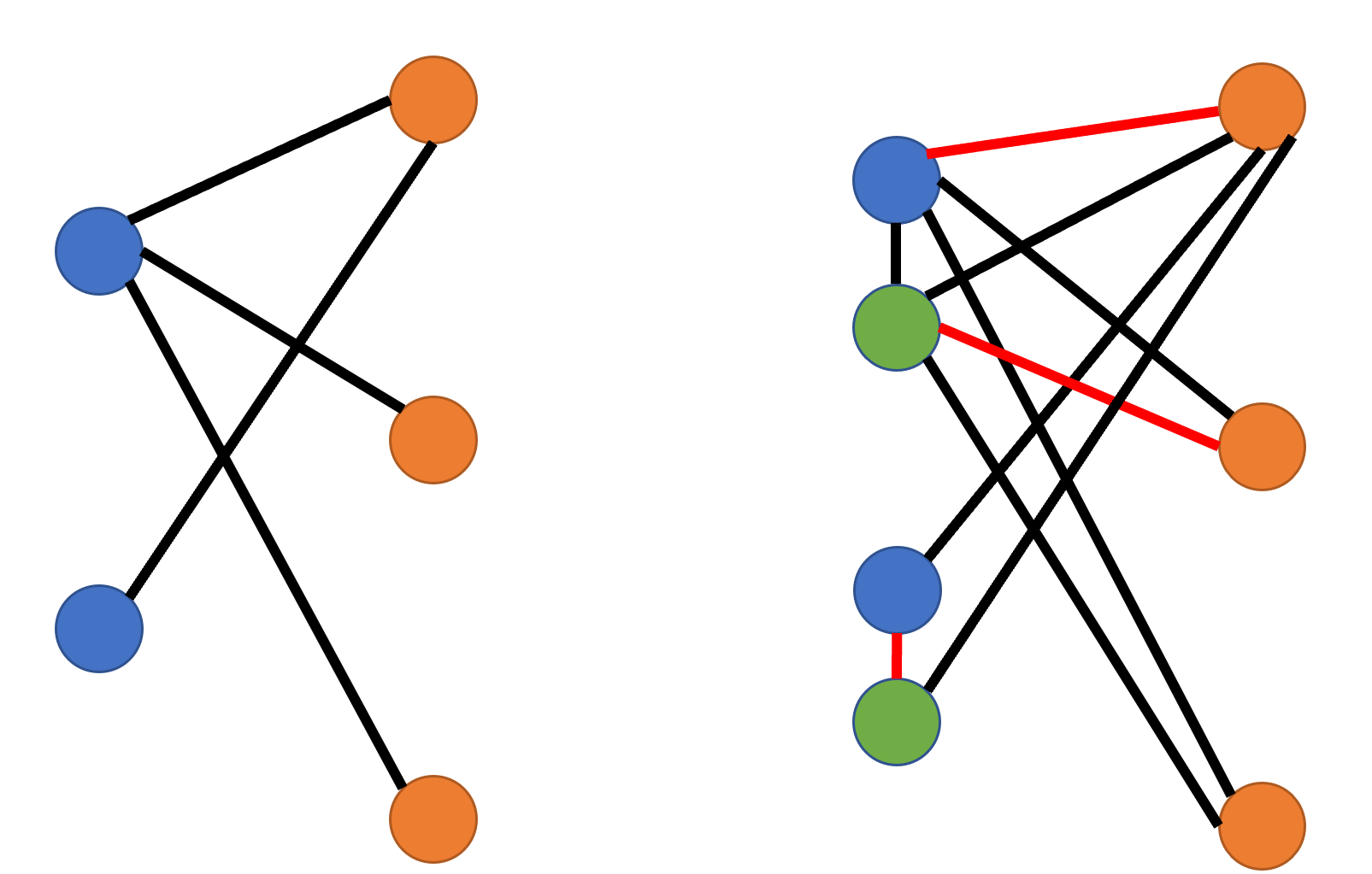
我们把每个男的(蓝点)拆成两个点,一个蓝的一个绿的(不用在意为什么是绿的,绿的健康),然后蓝的原来能跟哪些妹子好,绿的都能把他绿了,也相应地建边。
然后蓝的绿的也连边,表明他们虽然是不同的人格,但在同一条线上,是同一个人嘛。此时整个图的匹配数,最少也是n了,男的自己跟自己匹配,跟五指姑娘幸福快乐地生活下去。
那什么时候匹配数会增加的,对于一个男的来说,无非就是两个人格都匹配到了妹子,此时就不用直接跟自己搞基了。否则只有一个人格匹配了妹子的话,那另外一个人格,没得搞基了,又没有找到妹子,只能孤独终老,此时一加一减,匹配数不变。
所以最终就是看新图中的最大匹配是多少,然后减去n,就是我们想要求的最终答案。

1 #include<cstdio> 2 #include<queue> 3 using namespace std; 4 const int N=511,M=5e4+11; 5 struct Side{ 6 int v,ne; 7 }S[M<<1]; 8 queue<int> q; 9 char mp[N]; 10 int n,n2,nm,m,sn,fn,head[N],fa[N],pp[N],pre[N],col[N],flo[N]; 11 void init(){ 12 sn=fn=0; 13 n2=n*2;nm=n2+m; 14 for(int i=0;i<=nm;i++){ 15 head[i]=-1; 16 pp[i]=flo[i]=0; 17 } 18 } 19 void add(int u,int v){ 20 S[sn].v=v; 21 S[sn].ne=head[u]; 22 head[u]=sn++; 23 } 24 int find(int x){ 25 return fa[x]==x ? x : fa[x]=find(fa[x]); 26 } 27 int flca(int x,int y){ 28 ++fn; 29 x=find(x);y=find(y); 30 while(flo[x]!=fn){ 31 flo[x]=fn; 32 x=find(pre[pp[x]]); 33 if(y){ 34 int temp=x;x=y;y=temp; 35 } 36 } 37 return x; 38 } 39 void blossom(int x,int y,int z){ 40 while(find(x)!=z){ 41 pre[x]=y; 42 y=pp[x]; 43 if(col[y]==2){ 44 col[y]=1; 45 q.push(y); 46 } 47 if(find(x)==x) fa[x]=z; 48 if(find(y)==y) fa[y]=z; 49 x=pre[y]; 50 } 51 } 52 int aug(int u){ 53 for(int i=0;i<=nm;i++){ 54 fa[i]=i; 55 col[i]=pre[i]=0; 56 } 57 while(!q.empty()) q.pop(); 58 q.push(u); 59 col[u]=1; 60 while(!q.empty()){ 61 u=q.front(); 62 q.pop(); 63 for(int i=head[u],v;~i;i=S[i].ne){ 64 v=S[i].v; 65 if(find(u)==find(v)||col[v]==2) continue; 66 if(!col[v]){ 67 pre[v]=u;col[v]=2; 68 if(!pp[v]){ 69 for(int x=v,y;x;x=y){ 70 y=pp[pre[x]]; 71 pp[x]=pre[x]; 72 pp[pre[x]]=x; 73 } 74 return 1; 75 } 76 col[pp[v]]=1;q.push(pp[v]); 77 }else{ 78 int fl=flca(u,v); 79 blossom(u,v,fl); 80 blossom(v,u,fl); 81 } 82 } 83 } 84 return 0; 85 } 86 int main(){ 87 int t,x; 88 scanf("%d",&t); 89 while(t--){ 90 scanf("%d%d",&n,&m); 91 init(); 92 for(int i=1;i<=n;i++){ 93 add(i,i+n); 94 add(i+n,i); 95 scanf("%s",mp+1); 96 for(int j=1;j<=m;j++) if(mp[j]=='1'){ 97 add(i,n2+j); 98 add(n2+j,i); 99 add(i+n,n2+j); 100 add(n2+j,i+n); 101 } 102 } 103 int ans=0; 104 for(int i=1;i<=nm;i++) if(!pp[i]) ans+=aug(i); 105 // for(int i=1;i<=n;i++) printf("%d ",pp[i]); 106 // printf("\n"); 107 // for(int i=1;i<=n;i++) printf("%d ",pp[i+n]); 108 // printf("\n"); 109 printf("%d\n",ans-n); 110 } 111 return 0; 112 } 113 //https://codeforces.com/contest/1089
然后一般图一些其他东西。
以下名词的概念,在二分图中在进行解释,这里就不重复了。
最大权匹配:这个太要人命了,找也找不到相关讲解的博客,找了板子也一脸懵,两百多行的代码量简直是在上树,这就贴个板子以示尊重。
静听风吟。的图论:带花树算法-一般图最大权匹配
最小路径覆盖 :转换成二分图,把原图中的所有节点分成两份(X集合为i,Y集合为i'),如果原来图中有i->j的有向边,则在二分图中建立i->j'的有向边。最终|最小路径覆盖|=|V|-|M|
最小顶点覆盖:这是个NP Hard的问题。
最大独立集跟最大团:最大独立集就是补图的最大团
求最大团的思路就是就是暴力搜索加剪枝,复杂度不好分析,理论上大概就是n*2n实际上当然没那么大,实现上有两种实现方法。
主要思想就都是,从后往前遍历,然后当前点必须要,然后看跟之前的点集能不能组成一个更大团,相应的剪枝就是记录下之前点集的最大团大小。
第二种实现方法的优化就是,记录下当前节点能走到哪些点,然后再看那些点又能走到哪些点。
Maximum CliqueHDU - 1530
裸题

1 #include<cstdio> 2 const int N=55; 3 bool mp[N][N]; 4 int n,ans,mcq[N],vis[N]; 5 bool dfs(int pos,int num){ 6 if(num>ans){ 7 //此时vis记录的点就是最大团内的点 8 ans=num; 9 return true; 10 } 11 for(int i=pos+1,j;i<=n;i++){ 12 if(num+mcq[i]<=ans) return false;//如果当前这些点全可以加入 13 //之前这个最大团还没答案大的话,没必要再往下搜索了 14 for(j=num-1;j>=0;j--) if(!mp[i][vis[j]]) break; 15 if(j==-1){ 16 vis[num]=i; 17 if(dfs(i,num+1)) return true; 18 } 19 } 20 return false; 21 } 22 int maxcq(){ 23 ans=0; 24 for(int i=n;i>=1;i--){ 25 vis[0]=i; 26 dfs(i,1);//当前节点必须要,找[vi,vi+1..vn]这个点集能组成的最大团 27 mcq[i]=ans; 28 } 29 return ans; 30 } 31 int main(){ 32 while(~scanf("%d",&n)&&n){ 33 for(int i=1;i<=n;i++) 34 for(int j=1;j<=n;j++) 35 scanf("%d",&mp[i][j]); 36 printf("%d\n",maxcq()); 37 } 38 return 0; 39 }

1 #include<cstdio> 2 const int N=55; 3 bool mp[N][N]; 4 int n,ans,mcq[N]; 5 bool dfs(int *adj,int tot,int num){ 6 if(tot==0){ 7 if(num>ans){ 8 ans=num; 9 return true; 10 } 11 return false; 12 } 13 int temp[N],cnt; 14 for(int i=0;i<tot;i++){ 15 if(num+tot-i<=ans) return false;//剩下的点全要还没答案大,也不用往下搜索了 16 if(num+mcq[adj[i]]<=ans) return false;//跟未优化的num+mcq[i]<=ans同理 17 cnt=0; 18 for(int j=i+1;j<tot;j++) if(mp[adj[i]][adj[j]]) temp[cnt++]=adj[j]; 19 if(dfs(temp,cnt,num+1)) return true; 20 } 21 return false; 22 } 23 int maxcq(){ 24 int adj[N],cnt; 25 ans=0; 26 for(int i=n;i>=1;i--){ 27 cnt=0; 28 for(int j=i+1;j<=n;j++) if(mp[i][j]) adj[cnt++]=j;//把它相连的点保存下来 29 dfs(adj,cnt,1); 30 mcq[i]=ans; 31 } 32 return ans; 33 } 34 int main(){ 35 while(~scanf("%d",&n)&&n){ 36 for(int i=1;i<=n;i++) 37 for(int j=1;j<=n;j++) 38 scanf("%d",&mp[i][j]); 39 printf("%d\n",maxcq()); 40 } 41 return 0; 42 }
Graph Coloring POJ - 1419
求最大独立集,建补图,然后模板跑一下记录一下相应的答案。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=111; 5 bool mp[N][N]; 6 int n,ans,mcq[N],vis[N],ids[N]; 7 bool dfs(int *adj,int tot,int num){ 8 if(tot==0){ 9 if(num>ans){ 10 ans=num; 11 for(int i=0;i<num;i++) ids[i]=vis[i]; 12 return true; 13 } 14 return false; 15 } 16 int temp[N],cnt; 17 for(int i=0;i<tot;i++){ 18 if(num+tot-i<=ans) return false; 19 if(num+mcq[adj[i]]<=ans) return false; 20 cnt=0; 21 for(int j=i+1;j<tot;j++) if(mp[adj[i]][adj[j]]) temp[cnt++]=adj[j]; 22 vis[num]=adj[i]; 23 if(dfs(temp,cnt,num+1)) return true; 24 } 25 return false; 26 } 27 int maxcq(){ 28 int adj[N],cnt; 29 ans=0; 30 for(int i=n;i>=1;i--){ 31 cnt=0; 32 vis[0]=i; 33 for(int j=i+1;j<=n;j++) if(mp[i][j]) adj[cnt++]=j; 34 dfs(adj,cnt,1); 35 mcq[i]=ans; 36 } 37 return ans; 38 } 39 int main(){ 40 int t,m,u,v; 41 scanf("%d",&t); 42 while(t--){ 43 scanf("%d%d",&n,&m); 44 for(int i=1;i<=n;i++) 45 for(int j=1;j<=n;j++) 46 mp[i][j]=true; 47 while(m--){ 48 scanf("%d%d",&u,&v); 49 mp[u][v]=mp[v][u]=false; 50 } 51 maxcq(); 52 printf("%d\n",ans); 53 sort(ids,ids+ans); 54 for(int i=0;i<ans;i++) printf("%d%c",ids[i]," \n"[i==ans]); 55 } 56 return 0; 57 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号