数论之广义斐波那契循环节

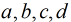
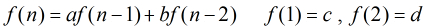
广义斐波那契：，满足，求

acdreamers大佬的推导证明：广义Fibonacci数列找循环节

首先我们肯定知道，这是可以写成矩阵快速幂的形式，问题就在于，n很大的时候呢？

这就是有一个降幂公式，对于要模的数x,循环节就是，∏(pi-1)(pi+1) *x/∏pi

也就是把x的所有质因子pi，把(pi-1)*(pi+1)全乘起来，然后乘上x/pi

至于为什么，这个就不知道了。这个是由txdywjy灵机一闪，猜测出来的积性函数。

直接作为模板用上了。

 所以牛客多校第5场的B可以直接降幂做，https://ac.nowcoder.com/acm/contest/885/B

  1 #include<cstdio>
  2 #include<cstring>
  3 typedef long long ll;
  4 const int N=1000000+10;
  5 struct Node{
  6     int r,c;
  7     ll jz[3][3];
  8     Node(){
  9         memset(jz,0,sizeof(jz));
 10     }
 11 };
 12 ll x0,x1,a,b,n,md,mmd;
 13 char s[N];
 14 int pn,pri[100000+10];
 15 void init(){
 16     ll lim;
 17     for(int i=2;i<=100000;i++){
 18         if(!pri[i]) pri[pn++]=i;
 19         for(int j=0;j<pn;j++){
 20             lim=1ll*i*pri[j];
 21             if(lim>100000) break;
 22             pri[lim]=1;
 23             if(i%pri[j]==0) break; 
 24         }
 25     }
 26 }
 27 ll solve(ll x){
 28     ll ans1=1,ans2=1,xx=x;
 29     for(int i=0;i<pn;i++){
 30         if(1ll*pri[i]*pri[i]>x) break;
 31         if(x%pri[i]==0){
 32             ans1*=(pri[i]-1)*(pri[i]+1);
 33             ans2*=pri[i];
 34             while(x%pri[i]==0) x/=pri[i];
 35         }
 36     }
 37     if(x>1){
 38         ans1*=(x-1)*(x+1);
 39         ans2*=x;
 40     }
 41     return xx/ans2*ans1;
 42 }
 43 ll mul(ll x,ll y,ll z){
 44     x%=z;
 45     y%=z;
 46     ll ans=0;
 47     while(y){
 48         if(y&1){
 49             ans+=x;
 50             if(ans>=z) ans-=z;
 51         }
 52         x<<=1;
 53         if(x>=z) x-=z;
 54         y>>=1;
 55     }
 56     return ans;
 57 }
 58 Node Nmul(Node x,Node y,ll z){
 59     Node ans;
 60     ans.r=x.r;
 61     ans.c=y.c;
 62     for(int i=0;i<x.r;i++)
 63         for(int j=0;j<y.c;j++)
 64             for(int k=0;k<x.c;k++){
 65                 ans.jz[i][j]+=mul(x.jz[i][k],y.jz[k][j],z);
 66                 if(ans.jz[i][j]>=z) ans.jz[i][j]-=z;
 67             }
 68     return ans;
 69 }
 70 Node Npow(Node x,ll y,ll z){
 71     Node ans;
 72     ans.r=x.r;
 73     ans.c=x.c;
 74     for(int i=0;i<ans.c;i++) ans.jz[i][i]=1;
 75     while(y){
 76         if(y&1) ans=Nmul(ans,x,z);
 77         x=Nmul(x,x,z);
 78         y>>=1;
 79     }
 80     return ans;
 81 }
 82 int main(){
 83     init();
 84     while(~scanf("%lld%lld%lld%lld",&x0,&x1,&a,&b)){
 85         scanf("%s%lld",s,&md);
 86         mmd=solve(md);
 87         n=0;
 88         int lens=strlen(s);
 89         for(int i=0;i<lens;i++){
 90             n=mul(n,10,mmd)+s[i]-'0'; 
 91             if(n>=mmd) n-=mmd;
 92         }
 93         Node A,T;
 94         A.r=2;
 95         A.c=1;
 96         A.jz[0][0]=x1;
 97         A.jz[1][0]=x0;
 98         T.r=2;
 99         T.c=2;
100         T.jz[0][0]=a;
101         T.jz[0][1]=b;
102         T.jz[1][0]=1;
103         if(n>1){
104             T=Npow(T,n-1,md);
105             A=Nmul(T,A,md);
106         }
107         printf("%lld\n",A.jz[0][0]);
108     }
109     return 0;
110 }
降幂板子

 但这题，n明确给出了，我们也可以用十进制的快速幂来处理指数来做。

 1 #include<cstdio>
 2 #include<cstring>
 3 typedef long long ll;
 4 const int N=1000000+10;
 5 struct Node{
 6     int r,c;
 7     ll jz[3][3];
 8     Node(){
 9         memset(jz,0,sizeof(jz));
10     }
11 };
12 ll x0,x1,a,b,n,md;
13 char s[N];
14 Node Nmul(Node x,Node y,ll z){
15     Node ans;
16     ans.r=x.r;
17     ans.c=y.c;
18     for(int i=0;i<x.r;i++)
19         for(int j=0;j<y.c;j++)
20             for(int k=0;k<x.c;k++){
21                 ans.jz[i][j]+=x.jz[i][k]*y.jz[k][j]%z;
22                 if(ans.jz[i][j]>=z) ans.jz[i][j]-=z;
23             }
24     return ans;
25 }
26 Node Npow(Node x,ll y,ll z){
27     Node ans;
28     ans.r=x.r;
29     ans.c=x.c;
30     for(int i=0;i<ans.c;i++) ans.jz[i][i]=1;
31     while(y){
32         if(y&1) ans=Nmul(ans,x,z);
33         x=Nmul(x,x,z);
34         y>>=1;
35     }
36     return ans;
37 }
38 int main(){
39     while(~scanf("%lld%lld%lld%lld",&x0,&x1,&a,&b)){
40         scanf("%s%lld",s,&md);
41         Node A,T,B;
42         B.r=2;B.c=2;
43         for(int i=0;i<B.c;i++) B.jz[i][i]=1;
44         A.r=2;A.c=1;
45         A.jz[0][0]=x1;
46         A.jz[1][0]=x0;
47         T.r=2;T.c=2;
48         T.jz[0][0]=a;
49         T.jz[0][1]=b;
50         T.jz[1][0]=1;
51         n=0;
52         int lens=strlen(s);
53         for(int i=lens-1;i>=0;i--){
54             if((s[i]-'0')!=0) B=Nmul(B,Npow(T,s[i]-'0',md),md); 
55             T=Npow(T,10,md);
56         }
57         A=Nmul(B,A,md);
58         printf("%lld\n",A.jz[1][0]);
59     }
60     return 0;
61 }
十进制快速幂

不过运行时间上，降幂是更快的，然后举一题需要降幂的例子。

Best Solver

HDU - 5451 

题意：已知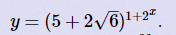，给你整数x,和一个素数M，求[y]%M

 对于这题，首先也是先写出矩阵快速幂的形式，这个很好写，就不多说了，

然后这里的指数是很长的，要求的，不能拆成十进制，所以需要降幂，因为m是质数，循环节就是(m-1)*(m+1)

最后还有个根号六要处理，引用别人的

首先(5+2sqrt(6))^n + (5-2sqrt(6))^n 是一个整数，且(5-2sqrt(6))^n < 1

所以 (5+2sqrt(6))^n + (5-2sqrt(6))^n = x + y sqrt(6) + x - ysqrt(6)

所以算出 (5+2sqrt(6))^n的整数部分x，答案就是2*x-1

 1 #include<cstdio>
 2 #include<cstring>
 3 typedef long long ll;
 4 struct Node{
 5     int r,c;
 6     ll jz[3][3];
 7     Node(){
 8         memset(jz,0,sizeof(jz));
 9     }
10 };
11 Node Nmul(Node x,Node y,ll z){
12     Node ans;
13     ans.r=x.r;
14     ans.c=y.c;
15     for(int i=0;i<x.r;i++)
16         for(int j=0;j<y.c;j++)
17             for(int k=0;k<x.c;k++){
18                 ans.jz[i][j]+=x.jz[i][k]*y.jz[k][j]%z;
19                 if(ans.jz[i][j]>=z) ans.jz[i][j]-=z;
20             }
21     return ans;
22 }
23 Node Npow(Node x,ll y,ll z){
24     Node ans;
25     ans.r=x.r;
26     ans.c=x.c;
27     for(int i=0;i<ans.c;i++) ans.jz[i][i]=1;
28     while(y){
29         if(y&1) ans=Nmul(ans,x,z);
30         x=Nmul(x,x,z);
31         y>>=1;
32     }
33     return ans;
34 }
35 ll poww(ll x,ll y,ll z){
36     ll ans=1;
37     while(y){
38         if(y&1) ans=ans*x%z;
39         x=x*x%z;
40         y>>=1; 
41     }
42     return ans;
43 }
44 int main(){
45     int t=1,C,md;
46     ll n,mmd;
47     scanf("%d",&C);
48     while(t<=C){
49         scanf("%lld%d",&n,&md);
50         mmd=1ll*md*md-1;
51         Node A,T;
52         A.r=2;A.c=1;
53         A.jz[0][0]=5;
54         A.jz[1][0]=2;
55         T.r=2;T.c=2;
56         T.jz[0][0]=5;
57         T.jz[0][1]=12;
58         T.jz[1][0]=2;
59         T.jz[1][1]=5;
60         n=(poww(2,n,mmd)+1)%mmd;
61         if(n>1){
62             T=Npow(T,n-1,md);
63             A=Nmul(T,A,md);
64         }
65         printf("Case #%d: %lld\n",t++,(2ll*A.jz[0][0]-1+md)%md);
66     }
67     return 0;
68 }
板子板子

 

posted @ 2019-08-02 07:54  新之守护者  阅读(763)  评论(0)  编辑  收藏  举报