单调栈求全1(或全0)子矩阵的个数 洛谷P5300与或和 P3400仓鼠窝
爆零好爽,被中学生虐好爽,还好我毕业得早
求全1(或全0)子矩阵的个数,看了题解有好几种思路,我学了三种,但有两种不是很理解,而且也没另外那个跑得快,所以简单讲述一一下我会的那种来自Caro23333大佬的思路,传送门。
首先我们要知道,n*m矩阵的全部子矩阵的个数是C2n+1*C2m+1,因为n*m矩阵横的线就有n+1条,竖的线就有m+1条,而我们横的线任选两根,竖的线也任选两根就能组成一个矩阵了。我们求解的思路就是用总的矩阵数去减去不是全0(或者全1)的子矩阵数。那怎么去求出不是全0(或者全1)的子矩阵数?
n*m的矩阵,以(n,m)格子作为右下角的子矩阵就有n*m个,因为它的左上角可以在n*m个格子里任意取。现在我们要求不是全0(或者全1)的子矩阵数,那么就是看那些格子作为它的左上角,使得矩阵包含0(或者1)。
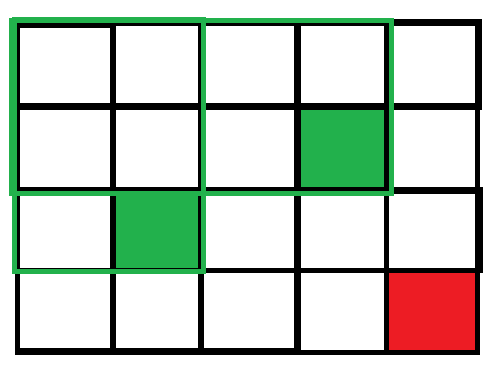
就比如上图,假设涂绿色的格子为0,其他全为1,现在我们求以红色格子为右下角,不是全1的子矩阵数。那么我们发现,以绿色区域内的格子作为左上角的子矩阵就不是全1的,因为他们的右下方存在着一个0。而绿色区域也很好求,假设一个绿色点是(x,y)那相应的绿色区域就是x*y。不过我们可以看出,绿色区域会有重复,这样的话会把一个区域算了多遍,那怎么处理这个重复的区域呢?
单调栈!我们从上到下,从左到右遍历所有格子,维护maxh[i]为i这一列为0的格子的最大行数,那么我们单调栈维护i,j,i<j有maxa[i]<maxa[j]。严格单调递减的栈,这样的话就使得,当前格子是0的话覆盖的区域不会与前面的重复,因为
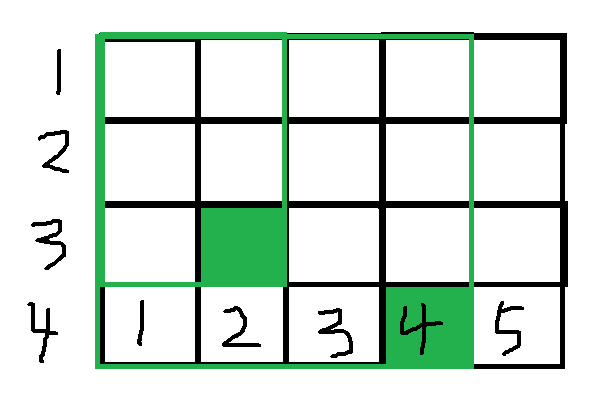
当遍历到,(4,4)这个格子的时候,maxh[4]=4,然后栈顶保持的是2,maxh[2]=3,所以把2弹出栈,这时栈顶元素是0,对(4,4)这个右下角产生贡献的绿色区域就是,res[0]+(4-0)*maxh[4],从图中看就是第二个绿色区域。
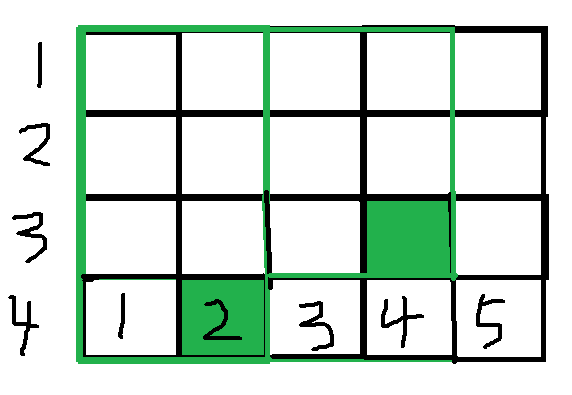
而当这个情况时,还是遍历到(4,4)这个格子的时候,maxh[4]=3,然后栈顶保持的是2,maxh[2]=4,所以2不用弹出栈,这时栈顶元素是2,对(4,4)这个右下角产生贡献的绿色区域就是res[2]+(4-2)*maxh[4]。从图中看就是,第一个绿色区域,以及第二个绿色区域不和第一个绿色区域重复的格子数。
所以可以知道res是什么了,res[i]就是前i列最下面的那个0能够贡献的格子,也是覆盖的区域,那么res[i]=res[栈顶元素]+(j-栈顶元素)*maxh[i]//相当于宽乘高,当遍历第i行第j列时的res[j]就是(i,j)这个格子作为右下角时,不是全1的子矩阵的左上角个数。

1 #include<cstdio> 2 typedef long long ll; 3 const int N=3233; 4 int a[N][N],sta[N],maxh[N]; 5 ll res[N]; 6 int main() 7 { 8 int n,m; 9 scanf("%d%d",&n,&m); 10 for(int i=1;i<=n;i++) 11 for(int j=1;j<=m;j++) 12 scanf("%d",&a[i][j]); 13 int top; 14 ll all=(1ll*n*(n+1)*m*(m+1))>>2,ans=0ll;//all总的方案数 15 for(int i=1;i<=n;i++) 16 { 17 sta[top=0]=0; 18 for(int j=1;j<=m;j++) 19 { 20 if(!a[i][j])//因为我们要求的是全1,所以维护这一列0的最大行数,也就是高度 21 maxh[j]=i; 22 while(top&&maxh[sta[top]]<=maxh[j]) 23 top--; 24 res[j]=res[sta[top]]+1ll*(j-sta[top])*maxh[j]; 25 ans+=res[j]; 26 sta[++top]=j; 27 } 28 } 29 printf("%lld\n",all-ans); 30 return 0; 31 }
这题就是把数拆成31位,每一位有对应的权值。

1 #include<cstdio> 2 typedef long long ll; 3 const int N=1108,mod=1000000007; 4 int n,cf2[32]={1},a[N][N],h[N][N]; 5 int sta[N],maxh[N]; 6 ll res[N]; 7 ll count(int k,int x) 8 { 9 for(int i=1;i<=n;i++) 10 maxh[i]=0; 11 int top=0; 12 ll ans=0; 13 for(int i=1;i<=n;i++) 14 { 15 sta[top=0]=0; 16 for(int j=1;j<=n;j++) 17 { 18 if(a[i][j]&cf2[k]) 19 h[i][j]=x; 20 else 21 h[i][j]=x^1; 22 if(!h[i][j]) 23 maxh[j]=i; 24 while(top&&maxh[sta[top]]<=maxh[j]) 25 top--; 26 res[j]=res[sta[top]]+1ll*(j-sta[top])*maxh[j]; 27 if(res[j]>=mod) 28 res[j]-=mod; 29 ans+=res[j]; 30 if(ans>=mod) 31 ans-=mod; 32 sta[++top]=j; 33 } 34 } 35 return ans; 36 } 37 int main() 38 { 39 for(int i=1;i<=30;i++) 40 cf2[i]=cf2[i-1]<<1; 41 scanf("%d",&n); 42 for(int i=1;i<=n;i++) 43 for(int j=1;j<=n;j++) 44 scanf("%d",&a[i][j]); 45 ll all=((1ll*n*(n+1)*n*(n+1))>>2)%mod; 46 ll ans1=0,ans2=0; 47 for(int k=0;k<=30;k++) 48 { 49 ans1+=((all-count(k,1)+mod)%mod)*1ll*cf2[k]; 50 if(ans1>=mod) 51 ans1%=mod; 52 ans2+=count(k,0)*1ll*cf2[k]; 53 if(ans2>=mod) 54 ans2%=mod; 55 } 56 printf("%lld %lld\n",ans1,ans2); 57 return 0; 58 }


