HDU - 3586 Information Disturbing 树形dp二分答案
HDU - 3586 Information Disturbing
题目大意:从敌人司令部(1号节点)到前线(叶子节点)的通信路径是一个树形结构,切断每条边的联系都需要花费w权值,现在需要你切断前线和司令部的连接,(就是所有叶子节点都到不了根节点),并且总花费不能超过m。问能够实行的方案中,最大花费的最小值,否则输出-1.
树形dp的题还是很好意识到用树形dp的,但最好是画一画图进行理解和推导,就像现在我随手画的图(第一次发现可以传图片)。
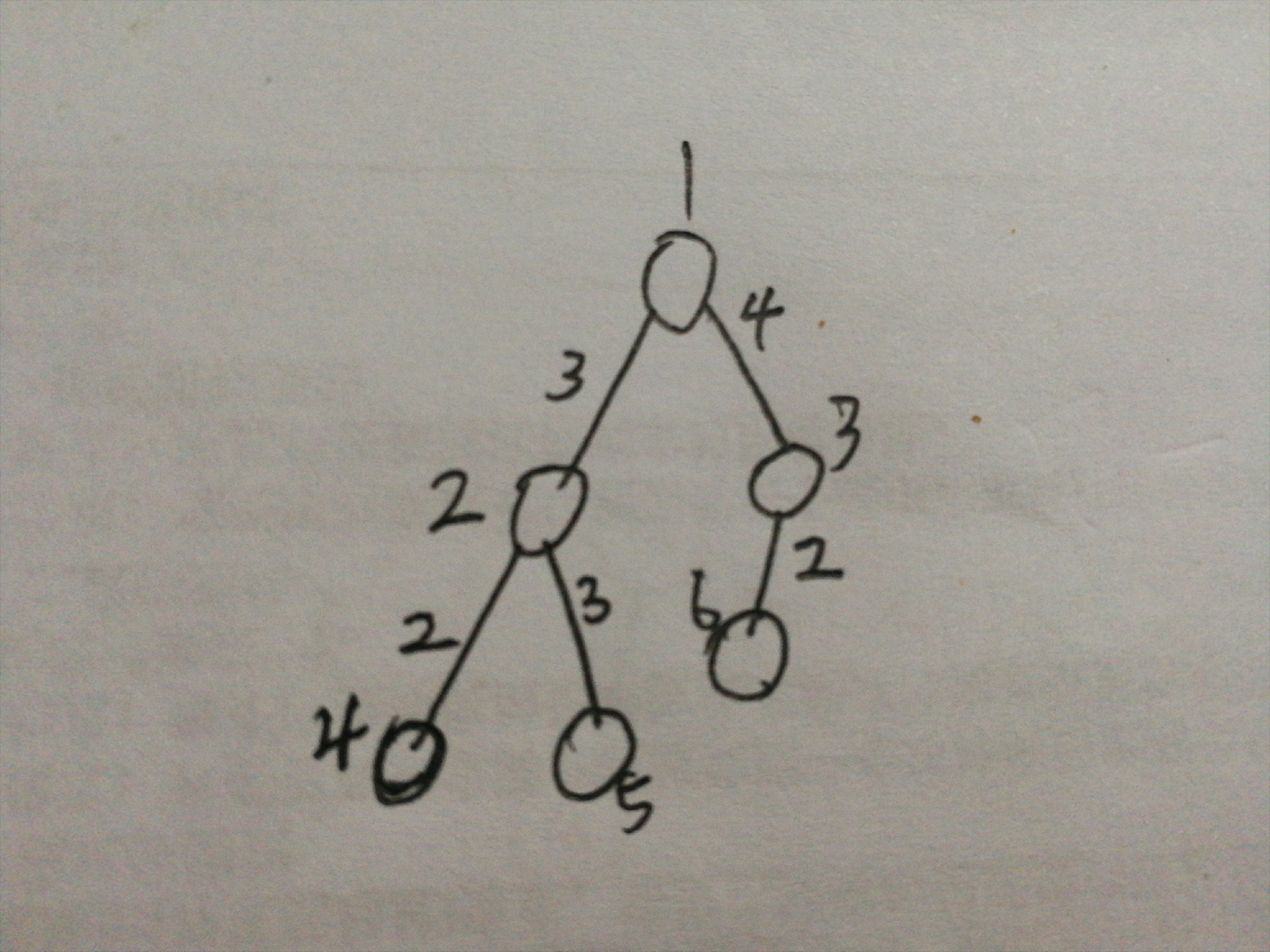 (画得有点小丑,问题不大)
(画得有点小丑,问题不大)
现在回到问题,就是我们需要切断1和4,5,6节点联系,那我们有几种选择呢,首先现在6节点,6节点只和3节点相连,3节点和1节点相连,那我们可以通过切断1和3的联系,或者是切断3和6的联系,来实现切断1和6的连接,很明显我们会选择3和6的联系,因为它们的权值较小。推理到左边,要切断1和4,5的联系就有,一.切断1和2的联系,二。切断2和3以及切断2和5的联系这两种,很明显我们会选择切断1和3的联系。我们可以发现如果我们把每个节点视为根节点的话,要切断它和叶子节点的关系无非有两种联系,切断它和它下一级的节点的联系,或者它下一级的节点切断和它所有节点的联系。我们用dp[i]来表示i节点切断它和它所有叶子节点的总花费最小值就有
 (字也丑。。。)
(字也丑。。。)
但现在问题是要找到的是一个最大花费的最小值,如果我们直接树形dp跑一遍的话就只能找到一个方案,并且其中的最大值不一定就是最小的,所以我们需要二分一个答案,然后用这个答案作为一个限制去跑树形dp看该方案可不可行?那么怎么实现这个限制呢?我想到的是如果一条边的权值已经大于限制值了,那就让它等于m+1,这样的话如果没有其他能代替它的更小的边,最终总花费肯定是大于m的,也就是方案不可行。其他细节详情见代码如下

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=1108; 6 struct Side{ 7 int v,ne,w; 8 }S[2*N]; 9 int sn,n,m,head[N],dp[N]; 10 void add(int u,int v,int c) 11 { 12 S[sn].v=v; 13 S[sn].w=c; 14 S[sn].ne=head[u]; 15 head[u]=sn++; 16 } 17 int dfs(int u,int f,int lim) 18 { 19 dp[u]=0; 20 for(int i=head[u];i!=-1;i=S[i].ne) 21 { 22 int v=S[i].v; 23 if(v!=f) 24 { 25 dfs(v,u,lim); 26 int cost=(S[i].w>lim ? m+1 : S[i].w);//如果权值超过限制,设为m+1 27 dp[u]+=min(dp[v],cost);//子节点的花费以及相连的边权值中取个最小值 28 //当前节点加上所有子节点需要切断和叶子节点的花费 29 } 30 } 31 if(dp[u]==0)//这个是用来判断它是不是叶子节点的 32 dp[u]=0x3f3f3f3f;//叶子节点的dp设个最大值,它的父节点只能切断和它相连的边 33 return dp[u]; 34 } 35 int main() 36 { 37 int a,b,w; 38 while(scanf("%d%d",&n,&m)&&(n||m)) 39 { 40 for(int i=0;i<=n;i++) 41 head[i]=-1; 42 int l=1001,r=0;//l所有边中的最小值,r所有边中的最大值 43 sn=0; 44 for(int i=1;i<n;i++) 45 { 46 scanf("%d%d%d",&a,&b,&w); 47 add(a,b,w); 48 add(b,a,w); 49 l=min(l,w); 50 r=max(r,w); 51 } 52 int ans=-1; 53 while(l<=r) 54 { 55 int mid=(l+r)>>1; 56 if(dfs(1,0,mid)<=m)//判断这个答案是否可行 57 ans=mid,r=mid-1;//可行的话,继续调小 58 else 59 l=mid+1; 60 } 61 printf("%d\n",ans); 62 } 63 return 0; 64 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号