bzoj2521 [Shoi2010]最小生成树
[Shoi2010]最小生成树
Time Limit: 10 Sec Memory Limit: 128 MB
Description
Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个n个点、m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外,他还知道,某一个图可能有多种不同的最小生成树。例如,下面图 3中所示的都是图 2中的无向图的最小生成树:
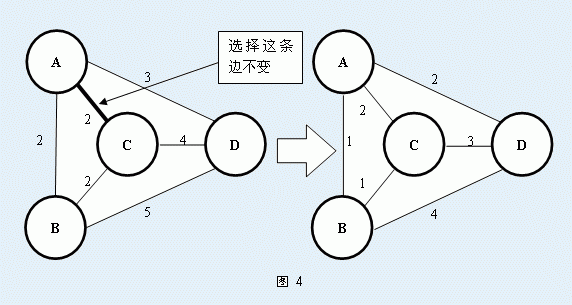
当然啦,这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB,至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中,你可以对这个无向图进行操作,一次单独的操作是指:先选择一条图中的边 P1P2,再把图中除了这条边以外的边,每一条的权值都减少1。如图 4所示就是一次这样的操作:
Input
输入文件的第一行有3个正整数n、m、Lab分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。
接下来m行依次描述标号为1,2,3…m的无向边,每行描述一条边。每个描述包含3个整数x、y、d,表示这条边连接着标号为x、y的点,且这条边的权值为d。
输入文件保证1<=x,y<=N,x不等于y,且输入数据保证这个无向图一定是一个连通图。
Output
输出文件只有一行,这行只有一个整数,即,使得标号为Lab边一定出现最小生成树中的最少操作次数。
Sample Input
4 6 1
1 2 2
1 3 2
1 4 3
2 3 2
2 4 4
3 4 5
Sample Output
1
HINT
第1个样例就是问题描述中的例子。
1<=n<=500,1<=M<=800,1<=D<10^6
首先kruskal瞎贪心过一会你就凉了。。。
例子:
1 2 2
2 1 2
1 3 1
2 3 6
强行6的边
所以你需要网络流。。。
因为你的目标是kruskal在你之前不连通,所以模拟这个过程,每条边权小于 (k+1)的边都建一条 (k+1-val) 的无向边。。。
然后网络流
#include<bits/stdc++.h>
using namespace std;
struct lpl{
int to, dis;
}lin;
const int maxn = 505, maxm = 805, INF = 0x7fffffff;
int cnt = -1, n, m, s, t, f, opt, A[maxm], B[maxm], val[maxm];
int layer[maxn];
vector<int> point[maxn];
vector<lpl> edge;
queue<int> q;
inline void connect(int a, int b, int c)
{
cnt++; lin.to = b; lin.dis = c; point[a].push_back(cnt); edge.push_back(lin);
cnt++; lin.to = a; lin.dis = c; point[b].push_back(cnt); edge.push_back(lin);
}
inline void putit()
{
scanf("%d%d%d", &n, &m, &opt);
for(int i = 1; i <= m; ++i) scanf("%d%d%d", &A[i], &B[i], &val[i]);
s = A[opt], t = B[opt], f = val[opt]; f++;
for(int i = 1; i <= m; ++i){
if(val[i] >= f) continue;
if(i == opt) continue;
connect(A[i], B[i], f - val[i]);
}
}
inline bool bfs()
{
int now, qwe; memset(layer, 0, sizeof(layer));
q.push(s); layer[s] = 1;
while(!q.empty()){
now = q.front(); q.pop();
for(int i = point[now].size() - 1; i >= 0; --i){
qwe = edge[point[now][i]].to;
if(layer[qwe] || edge[point[now][i]].dis <= 0) continue;
layer[qwe] = layer[now] + 1; q.push(qwe);
}
}
return layer[t];
}
int dfs(int a, int w)
{
if(w == 0 || a == t) return w;
int ret = 0;
for(int i = point[a].size() - 1; i >= 0; --i){
int now = point[a][i];
if(edge[now].dis <= 0 || layer[edge[now].to] != layer[a] + 1) continue;
int tmp = dfs(edge[now].to, min(edge[now].dis, w));
ret += tmp; edge[now].dis -= tmp; edge[now ^ 1].dis += tmp; w -= tmp;
if(!w) break;
}
return ret;
}
inline int Dinic()
{
int ret = 0;
while(bfs()) ret += dfs(s, INF);
return ret;
}
int main()
{
putit();
cout << Dinic();
return 0;
}
心如花木,向阳而生。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号