Codeforces Fix a Tree
Fix a Tree
time limit per test2 seconds
A tree is an undirected connected graph without cycles.
Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, ..., pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).

For this rooted tree the array p is [2, 3, 3, 2].
Given a sequence p1, p2, ..., pn, one is able to restore a tree:
There must be exactly one index r that pr = r. A vertex r is a root of the tree.
For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.
A sequence p1, p2, ..., pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences (1,2,2), (2,3,1) and (2,1,3) are not valid.
You are given a sequence a1, a2, ..., an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.
Input
The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n).
Output
In the first line print the minimum number of elements to change, in order to get a valid sequence.
In the second line, print any valid sequence possible to get from (a1, a2, ..., an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.
Examples
input
4
2 3 3 4
output
1
2 3 4 4
input
5
3 2 2 5 3
output
0
3 2 2 5 3
input
8
2 3 5 4 1 6 6 7
output
2
2 3 7 8 1 6 6 7
Note
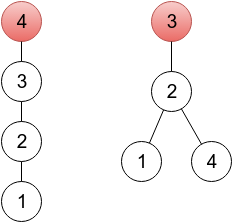
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (because p4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.
In the second sample, the given sequence is already valid.
大概意思是: 给出 n 个结点的父亲,问至少修改多少个结点的父亲,能使整张图变成 一棵树(根的父亲为自己),要求输出任一方案。 其中 1 ≤ n ≤ 200000。
我的想法是你先按最小生成树的方法生成树,然后找一个点为根节点,有现成的就用,没有就选一个。 然后把每棵树都连起来就成了一棵新的树了。。。
写完以后很开心的发现1A了。。然后去看了看题解。。。
别人的方法是: 思考环和链的答案 图的各个弱连通块是环 + 内向树,或者树/环。 先用拓扑排序把内向树消掉 剩下来的是一些环,每个环随便选一个结点当根,然后再把所有的根连 在一起。 答案是环数-(是否存在自环)
其实我也没怎么看懂,我觉得道理应该差不多吧 ```c++
include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int n, root, tot, fa[maxn], ini[maxn];
bool flag[maxn];
set
set
inline int read()
{
int s = 0, w = 1; char ch = getchar();
while(ch <= '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
int find(int t){return t == fa[t] ? t : fa[t] = find(fa[t]);}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) ini[i] = read(), fa[i] = i;
for(int A, B, i = 1; i <= n; ++i){
A = find(i); B = find(ini[i]); if(A == B) continue;
fa[A] = B; flag[i] = true;
}
for(int i = 1; i <= n; ++i){s.insert(find(fa[i])); if(i == ini[i]) root = i;}
for(iter = s.begin(); iter != s.end(); ++iter) tot++;
if(!root){
for(int i = 1; i <= n; ++i){
if(flag[i]) continue;
root = i; tot++; flag[i] = true; ini[i] = i; break;
}
}
printf("%d\n", tot - 1);
for(int i = 1; i <= n; ++i){
if(flag[i]) printf("%d ", ini[i]);
else printf("%d ", root);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号