bzoj4903 [Ctsc2017]吉夫特

搞了半天这个东西要用 Lucas 定理啊。。。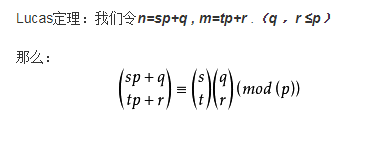 

学好这些姿势你就可以A了。。。
显然：

\[{0 \choose 1}=0\ \ \ {1 \choose 1}=1\ \ \ {1 \choose 0}=1\ \ \ {0 \choose 0}=1 \]

你一直用这个 Lucas 定理，又因为 mod = 2， 实际上就是把两个二进数数挨着挨着一位一位的比较。
所以你只要在过程中没有 \({0 \choose 1}\) 就好了。
在进一步就成了 \(n & m = m\) 就满足了。
你 dp 自己枚举一下岂不是很完美？

#include<bits/stdc++.h>
using namespace std;
const int maxn = 234567, mod = 1e9 + 7;
int n, ans, ini[maxn], lpl[maxn], pw[63];

inline void prepare()
{
	pw[1] = 1;
	for(int i = 2; i <= 20; ++i) pw[i] = pw[i - 1] * 2;
}

int main()
{
	prepare();
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) scanf("%d", &ini[i]);
	for(int now, i = n; i >= 1; --i){
		now = ini[i]; lpl[ini[i]] = 1;
		for(int j = now; j; ){
			j = (j - 1) & now;
			lpl[ini[i]] = (lpl[ini[i]] + lpl[j]) % mod;
		}
	}
	for(int i = 1; i <= n; ++i) ans = (ans + lpl[ini[i]]) % mod;
	cout << ans - n;
	return 0;
}