bzoj 2693 jzptab

jzptab

Time Limit: 10 Sec Memory Limit: 512 MB

Description

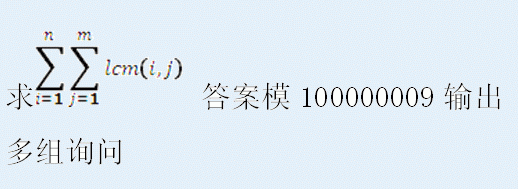
Input

一个正整数T表示数据组数
接下来T行 每行两个正整数 表示N、M

Output

T行 每行一个整数 表示第i组数据的结果

Sample Input

1

4 5

Sample Output

122

HINT

T <= 10000

N, M<=10000000

各种推公式的大爷强啊。。。。Orz 辣鸡题目。。。。mod是1e8+9 第一眼看成了1e9+7 调了半天 然后发现不对，看成1e9+9 还是调不出来，心态爆炸。。。。 然后就是日常卡long long。。。。
```c++

include<bits/stdc++.h>

using namespace std;
const int maxn = 1e7 + 5, maxm = 1e7, mod = 1e8 + 9;
int n, m, cnt, prime[maxn];
long long S[maxn];
bool not_prime[maxn];

inline void prepare()
{
S[1] = 1;
for(int i = 2; i <= maxm; ++i){
if(!not_prime[i]){
prime[++cnt] = i; S[i] = (i - (long long)i * i) % mod;
}
for(int j = 1; prime[j] * i <= maxm; ++j){
not_prime[prime[j] * i] = true;
if(i % prime[j] == 0){
S[prime[j] * i] = S[i] * prime[j] % mod;
break;
}
S[prime[j] * i] = S[prime[j]] * S[i] % mod;
}
}
for(int i = 1; i <= maxm; ++i) S[i] = (S[i] + S[i - 1]) % mod;
}

inline long long sum(long long a, long long b){
long long A = ((a + 1) * a >> 1) % mod, B = ((b + 1) * b >> 1) % mod;
return A * B % mod;
}

inline long long workk()
{
int last; long long ans = 0;
for(int D = 1; D <= n; D = last + 1){
last = min(n / (n / D), m / (m / D));
ans = (ans + sum(n / D, m / D) * (S[last] - S[D - 1]) % mod) % mod;
}
return (ans + mod) % mod;
}

int main()
{
prepare();
int T; scanf("%d", &T);
while(T--){
scanf("%d%d", &n, &m);
if(n > m) swap(n, m);
printf("%lld\n", workk());
}
return 0;
}