bzoj3527 [Zjoi2014]力

[Zjoi2014]力

Time Limit: 30 Sec Memory Limit: 256 MBSec Special Judge

Description

给出n个数qi，给出Fj的定义如下：

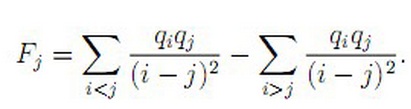
令Ei=Fi/qi，求Ei.

Input

第一行一个整数n。
接下来n行每行输入一个数，第i行表示qi。
n≤100000，0<qi<1000000000

Output

n行，第i行输出Ei。与标准答案误差不超过1e-2即可。

Sample Input

5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880

Sample Output

-16838672.693
3439.793
7509018.566
4595686.886
10903040.872

需要学习FFT乱搞卷积的请进。。。。这俩卷积很典型的啦~
表示我手贱。。。所以调试很刺激。。。。（请看样例。。。）
并且你需要在复数里面调试。。。（我已经死过一会了233）

#include<bits/stdc++.h>
#define pi acos(-1)
using namespace std;
const int maxn = 3e5 + 5;
int n, len, pl = 1;
int rev[maxn];
complex<double> g[maxn], a[maxn], b[maxn], ans1[maxn], ans2[maxn];

inline void putit()
{
	scanf("%d", &n); n--; double x;
	for(int i = 0; i <= n; ++i) {
		scanf("%lf", &x), a[i] = x, b[n - i] = x;
	}
}

inline void prepare()
{
	pl = 2 * n;
	for(int i = 1; i <= n; ++i) g[i] = ((1.0) / i / i);
	for(n = 1; n <= pl; n <<= 1) len++;
	for(int i = 0; i <= n; ++i) rev[i] = ((rev[i >> 1] >> 1) | ((i & 1) << (len - 1)));
}

inline void FFT(complex<double> *t, int mark)
{
	for(int i = 0; i < n; ++i) if(i < rev[i]) swap(t[i], t[rev[i]]);
	for(int i = 1; i < n; i <<= 1){
		complex<double> wn(cos(pi / i), mark * sin(pi / i));
		for(int j = 0; j < n; j = j + 2 * i){
			complex<double> w(1, 0);
			for(int k = j; k < j + i; ++k, w *= wn){
				complex<double> lin1 = t[k], lin2 = t[k + i] * w;
				t[k] = lin1 + lin2; t[k + i] = lin1 - lin2; 
			}
		}
	}
	if(mark == -1) for(int i = 0; i < n; ++i) t[i] /= n;
}

inline void workk()
{
	FFT(g, 1); FFT(a, 1); FFT(b, 1);
	for(int i = 0; i < n; ++i) ans1[i] = a[i] * g[i], ans2[i] = b[i] * g[i];
	FFT(ans1, -1); FFT(ans2, -1);
}

inline void print()
{
	n = pl / 2;
	for(int i = 0; i <= n; ++i) printf("%.3lf\n", ans1[i].real() - ans2[n - i].real());
}

int main()
{
	putit();
	prepare();
	workk();
	print();
	return 0;
}