OI中的快速傅里叶变换（FFT）

快速傅里叶变换（FFT）

                                                                              ———— LLppdd

前言

• 关于这篇文章

    非常高兴能有机会来探讨快速傅里叶变换，也就是大家熟知的 \(FFT\) 在 \(OI\) 中的运用。以前了解过一次 \(FFT\) ，现在过了几个月，数学和 \(OI\) 水平都有了一定的进步之后，再回过来重新思考它，应该有了更深的了解，所以准备写一篇较为详细的文章来和大家交流。
    我将尽我所能，在接下来的讲述中所涉及的内容给出尽量详细的推理和证明。谢谢大家。

• 你将会看到的内容

      关于复平面等一系列基础知识

      什么是快速傅里叶变换

      在 \(OI\) 中的快速傅里叶变换的实现原理

      在 \(OI\) 中的快速傅里叶变换的实现步骤解析

      在 \(OI\) 中的快速傅里叶变换的代码实现

• 阅读方法

    1.引用一段内容的表现方法：

（引用的内容）

    一般来说，直接引用的内容对本文的阅读并没有太大影响。当然，我也会选择尽量简洁明了的内容进行展示。

    2.我认为较为重要的地方：

        （较重要的内容）

    如果是我认为较重要的内容，那么可能对于后面的理解就比较重要了。

    3. 在代码实现部分，我将会引用代码块：

// My code

    4.同样地，比较重要的公式或者结论将会单独列出：

\[e^{i \pi}+1=0 \]

正文

1.关于复平面等一系列基础知识

• 什么是复数？

复数，为实数的延伸，它使任一多项式方程根。复数当中有个“虚数单位”\(i\)，它是\(-1\)的一个平方根，即 \(i^2=-1\)。任一复数都可表达为\(x+yi\)，其中 \(x\) 及 \(y\)皆为实数，分别称为复数之“实部”和“虚部”。
                                      ------- 节选自维基百科

    简单来说，复数由实部和虚部构成，表现形式为 \(x+yi\)。

• 什么是复平面？

数学中，复平面（complex plane）是用水平的实轴与垂直的虚轴建立起来的复数的几何表示。它可视为一个具有特定代数结构笛卡儿平面（实平面），一个复数的实部用沿着 x-轴的位移表示，虚部用沿着 y-轴的位移表示.                                       ------- 节选自维基百科

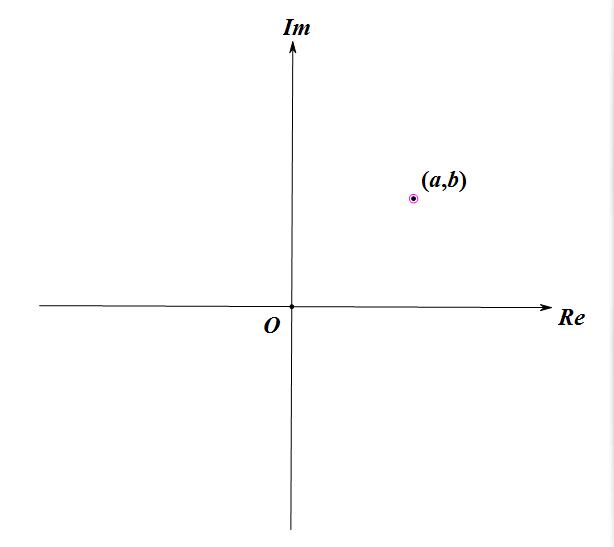
    在我们熟知的由 \(x\) 轴和 \(y\) 轴所构成的笛卡尔坐标系中，我们用 \((x,y)\) 来表示平面上的一个点。 类似的，我们可以描述出一个复平面。复平面上的每个点 \((x,y)\) 对应一个复数 \(x+yi\) 。也就意味着，我们用 \((x,y)\) 来表示一个复数 \(x+yi\)。

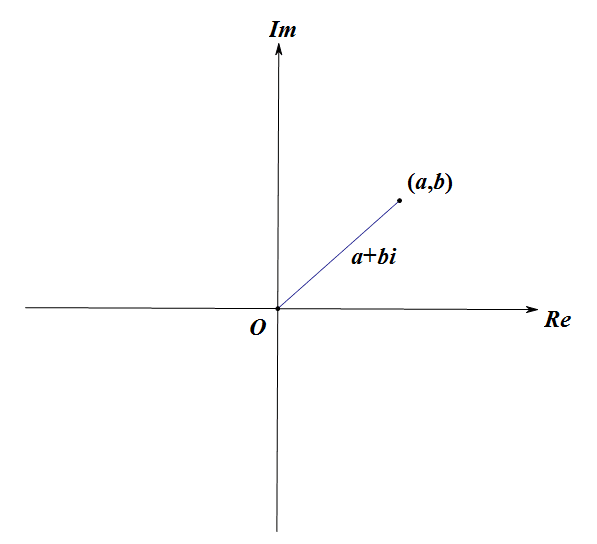
• 复数的基础运算法则
  
  
  \((a+bi)+(c+di)=(a+c)+(b+d)i\)
  \((a+bi)*(c+di)=(ac-bd)+(ad+bc)i\)

通过这个，我们可以引入复数的另一种表示方法：

    由 \((a+bi)+(c+di)=(a+c)+(b+d)i\)，

我们可以发现在复平面中，和向量的运算类似的:

    \((a,b) + (c,d) = (a+c, b + d)\)

但是我们可以发现我们并不能用类似的方法很简单的表示出乘法的运算，所以我们用另一种方法来表示它。

设 \(a=rcos\theta, b=rsin\theta\)     ( \(r\) 表示模长)
所以每个点就可以表示为 \((r,\theta)\)

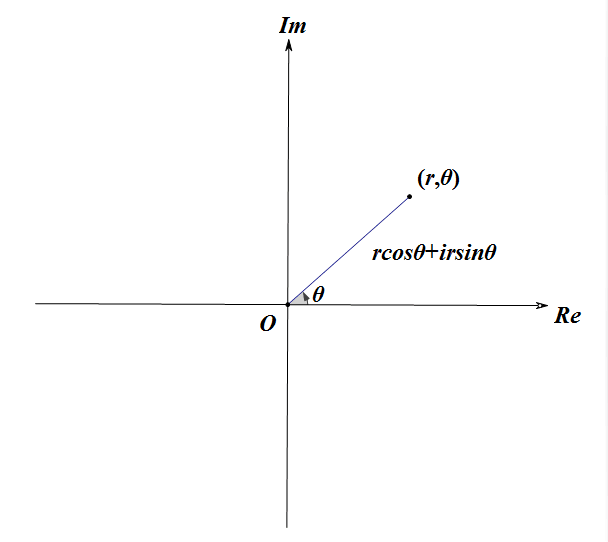
这样有什么好处呢？

对应 \((a+bi)*(c+di)=(ac-bd)+(ad+bc)i\)

\(=(r_1cos\theta_1r_2cos\theta_2-r_1sin\theta_1r_2sin\theta_2)+(r_1cos\theta_1r_2sin\theta_2+r_1sin\theta_1r_2cos\theta_2)i\)

\(=r_1r_2cos(\theta_1+\theta_2)+ir_1r_2sin(\theta_1+\theta_2)\)

显然，如上的和角公式的变化可以让我们轻易的得出：

\((r_1, \theta_1)*(r_2, \theta_2)=(r1r2, \theta_1+\theta_2)\)

对于以上两种不同的表示方法，我的理解是它们分别使复数的运算变的更为方便了，我也会在接下来的一些证明中频繁的使用它们。

• 什么是单位根？

数学上, \(n\) 次单位根是 \(n\) 次幂为1的复数。它们位于复平面的单位圆上，构成正 \(n\) 边形的顶点，其中一个顶点是1。
                                      ------- 节选自维基百科

    简单的说，方程 \(x^n=1\) 的复数根 \(x\) 我们称它为 \(n\) 次单位根。
    好，在这个定义下，我们可以进行一定的思考。
    满足 \(x^n = 1\) 的数有什么特点？ 有几个数满足 \(x^n=1\) ？
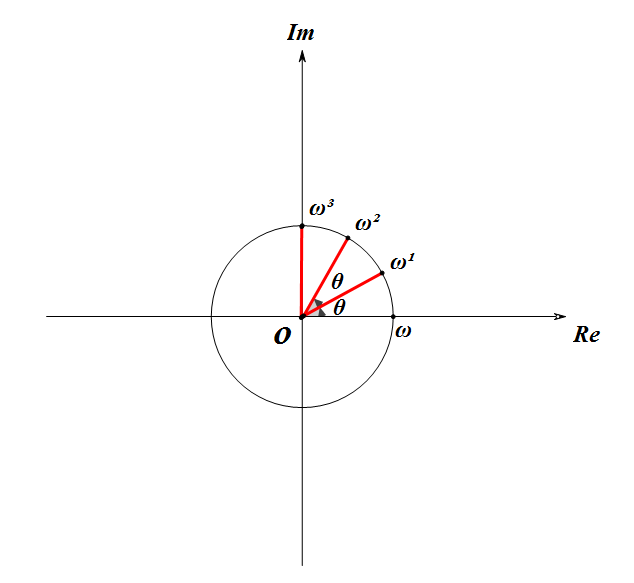
    我们设一个单位根为 \((1, \theta)\), 那么它的 \(n\) 次方为 \((1, n*\theta)\), 由题可得, $$n*\theta=2k\pi\ \ (k∈Z)$$

\[\Rightarrow \theta = \frac{2\pi}{n}k \ \ (k∈Z) \]

到了这里，我们可以形象的理解一下

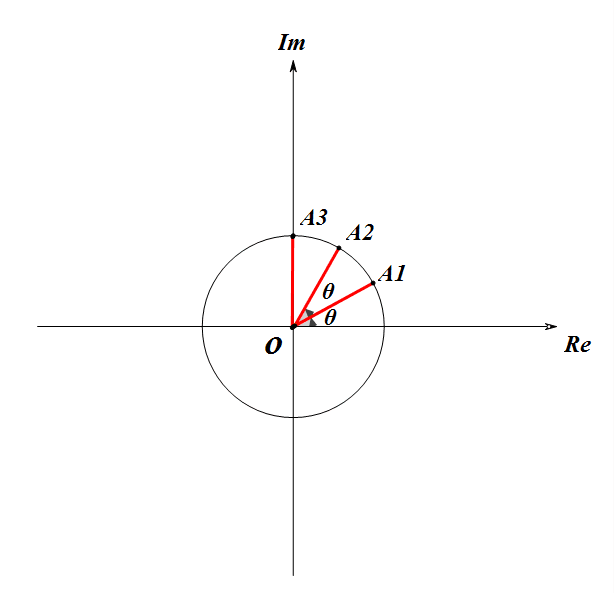
    显然有 \(n\) 个不同的值。
    表示方法：
        如果 \(\omega^k=1\) ，那么我们称 \(\omega\) 为 \(1\) 的 \(k\) 次单位根，记作 \(\omega_k^n\)。
        这个 \(n\) 的意义是单位根的标号 \((0 \thicksim n-1)\)

2.什么是快速傅里叶变换

傅里叶变换（法语：Transformation de Fourier、英语：Fourier transform）是一种线性积分变换，用于信号在时域（或空域）和频域之间的变换，在物理学和工程学中有许多应用。因其基本思想首先由法国学者约瑟夫·傅里叶系统地提出，所以以其名字来命名以示纪念。实际上傅里叶变换就像化学分析，确定物质的基本成分；信号来自自然界，也可对其进行分析，确定其基本成分。
                                      ------- 节选自维基百科

   这里是引用的维基百科上的简介，对于快速傅里叶变换本文不准备进行过多的介绍，个人认为在 \(OI\) 中的运用我们只用运用它的思想就足够了。

3.在 \(OI\) 中的快速傅里叶变换的实现原理

   首先我们要明白快速傅里叶变换在 \(OI\) 中是用来干什么的。首先它是用来解决很多有关多项式的问题的。最常见的就是计算卷积。而这里，我们用最简单的多项式乘法为例。
   多项式乘法的朴素计算方法复杂度应该是 \(O(n^2)\) 的，那么有没有更为优秀的方法呢? 在解决这个问题之前，我们可以先思考几个子问题。

• 如何表示一个多项式？
      最直接的是记录下每项对应的系数，举个例子：
      \(3x^3+2x+4\ \ \Rightarrow\ \ \ \{3, 0, 2, 4\}\)
      那么还有没有其他的方法呢？我们可以把每个多项式看做一个函数，那么对于一个 \(n\) 次函数，我们至少需要 \(n+1\) 才能确定它。（你至少需要两个不同的点才能确定一条一次函数），根据这个道理，我们就有了另一种新的方法来表示这个多项式：
      （假设 \(f(x) = 3x^3+2x+4\)）
      \(\Rightarrow \ \ \ \ \ \{ (x_1, f(x_1)), (x_2, f(x_2)), (x_3, f(x_3)), (x_4, f(x_4)) \}\)

   当我们有了这种新的方法以后，我们可以思考一下这个新的表示方法有什么好处。
    我们假设 \(F(x) = h(x)*g(x)\), 也就是说 \(h(x), g(x)\) 分别对应一个多项式，我们要求的是 \(F(x)\) 。
    假设它是个 \(n\) 次多项式，那么我们需要 \(n+1\) 个不同的点以及他们对应的值， 即 \(\{(x_1, F(x_1)), (x_2, F(x_2)), ..., (x_{n+1}, F(x_{n+1}))\}\)
    显然地，\(F(k) = h(k) * g(k)\), 也就是说，我们只需要
    \(\{(x_1, h(x_1)), (x_2, h(x_2)), ..., (x_{n+1}, h(x_{n+1}))\}\)
    \(\{(x_1, g(x_1)), (x_2, g(x_2)), ..., (x_{n+1}, g(x_{n+1}))\}\)
    然后将它们对应相乘就可以得到 \(F(x)\) 了。

    到了这里，就有了整个算法的主题思路了。
    1. 将两个多项式分别转化成点值的形式。
    2. 求出最终的多项式的点值表达形式。
    3. 将点值表达形式还原为对应的系数。

    上面的两个操作分别有它们对应的名字：
    将两个多项式分别转化成点值的形式。 \(DFT\) (离散傅里叶变换)。
    将点值表达形式还原为对应的系数。 \(IDFT\) (离散傅里叶反变换)。

4.在 \(OI\) 中的快速傅里叶变换的实现步骤解析

    我们依照上面给出的步骤依次分析。

• 将两个多项式分别转化成点值的形式
      首先，朴素算法的复杂度显然是 \(O(n^2)\) 的。所以这里介绍一种比较容易的方法。
  （假设多项式为 \(F(x)=a[0] + a[1] * x + a[2] * x^2 + a[3] * x^3 + ... + a[7] * x^7\)）
  那么我们可以对它进行一个变形：

\[(a[0] + a[2] * x^2 +a[4] * x^4 + a[6] * x^6) + (a[1]*x+a[3]*x^3+a[5] * x^5+a[7]*x^7) \]

\[(a[0] + a[2] * x^2 +a[4] * x^4 + a[6] * x^6) + x*(a[1]+a[3]*x^2+a[5] * x^4+a[7]*x^6) \]

设
    \(g(x)=a[0] + a[2] * x +a[4] * x^2 + a[6] * x^3\)
    \(h(x) = a[1]+a[3]*x^1+a[5] * x^2+a[7]*x^3\)

\[\Rightarrow F(x)=g(x^2)+x*h(x^2) \]

    同样地，我们可以处理 \(g(x)\) 和 \(h(x)\)。显然，用这样分治的思想要优秀许多，那么我们接下来再仔细观察一下这个过程。

\[\{a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]\} \]

\[\Downarrow \]

\[\{a[0],a[2],a[4],a[6]\}, \{a[1],a[3],a[5],a[7]\} \]

\[\Downarrow \]

\[\{a[0],a[4]\},\{a[2],a[6]\},\{a[1],a[5]\},\{a[3],a[7]\} \]

\[\Downarrow \]

\[\{a[0]\},\{a[4]\},\{a[2]\},\{a[6]\},\{a[1]\},\{a[5]\},\{a[3]\},\{a[7]\} \]

    我们提出首尾两项来进行一个对比：

\[\{a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7]\} \]

\[\{a[0], a[4], a[2], a[6], a[1], a[5], a[3], a[7]\} \]

    好像没有什么规律，那么在二进制下呢？

\[\{a[000], a[001], a[010], a[011], a[100], a[101], a[110], a[111]\} \]

\[\{a[000], a[100], a[010], a[110], a[001], a[101], a[011], a[111]\} \]

    仔细观察后可以发现，每个最终的位置上的数是他的标号在二进制下翻转后所对应的数。（这句话不是很容易理解，可以结合例子感性理解一下。）
    那么，为什么呢？
    我们可以思考一下每次操作的意义，第一次操作是把倒数第 \(1\) 位上是 \(0\) 的数放在前面，倒数第 \(1\) 位上是 \(1\) 的数放在后面； 第 \(2\) 次操作是把倒数第 \(2\) 位上是 \(0\) 的数放在前面，倒数第 \(2\) 位上是 \(1\) 的数放在后面 \(...\) 第 \(n\) 次操作是把倒数第 \(n\) 位上是 \(0\) 的数放在前面，倒数第 \(n\) 位上是 \(1\) 的数放在后面。
    这样来看，很容易发现倒数第 \(1\) 位上为 \(0\) 的数一定在倒数第 \(1\) 位上为 \(1\) 的数的前面，如果倒数第 \(1\) 位的数相同的情况下比较倒数第 \(2\) 位，以此类推。
    所以说，最后这个结果数组的排序方式是先比较最后 \(1\) 位，再比较倒数第 \(2\) 位 \(...\) 而原来的比较方式是先比较最开头的第 \(1\) 位，然后再比较顺数第 \(2\) 位 \(...\)。顺序刚好相反，所以就出现了最开始那个优美的性质。
    那么既然这样，我们就可以代替刚才的递归操作，直接从下往上计算。想必这样会更优秀一些。
    当然，要完成这个子任务，还有一个地方需要我们思考，我们怎样才可以快速方便的预处理出这个最终的位置关系。
    采用类似动态规划的思想。

    通过观察我们可以发现，对于每一个数的操作，我们可以保留最后一位不动，然后将前面的数翻转后的结果 "补" 在后面。由于前面的数是小于原数的，我们在处理当前数的时候一定是处理过前面截取的数的。

for(int i = 0; i < n; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));

    这里我们要注意，假设 \(n\) 在二进制意义下有 \(bit\) 位，那么\(rev\) 数组中的数在二进制下也一定是有 \(bit\) 位的。（所以我们才需要将 \(rev[i>>1]\)再\(>>1\)）。

    那么这个子任务大致就叙述完了，最后我们回过来可以发现，我们最开始一定要将原二项式补成二的整数次方项(为了保证可以顺利的分治到最后)。

• 求出最终的多项式的点值表达形式。

for(int i = 0; i <= n; ++i) c[i] = a[i] * b[i];

• 将点值表达形式还原为对应系数

    我们先把第一步做的事情用矩阵来描述一下（假设原系数为 \(a[i]\), 求得的每个点值为 \(y[i]\)）：

\[\left[\begin{matrix} y[0] \\ y[1] \\ y[2]\\ y[3]\\ \vdots\\ y[n-1]\\ \end{matrix}\right] {=} \left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right] \left[\begin{matrix} a[0] \\ a[1] \\ a[2]\\ a[3]\\ \vdots\\ a[n-1]\\ \end{matrix}\right] \]

显然的，我们需要构造一个逆矩阵。

\[` {\left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right]}^{-1} \left[\begin{matrix} y[0] \\ y[1] \\ y[2]\\ y[3]\\ \vdots\\ y[n-1]\\ \end{matrix}\right] {=} {\left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right]}^{-1} \left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right] \left[\begin{matrix} a[0] \\ a[1] \\ a[2]\\ a[3]\\ \vdots\\ a[n-1]\\ \end{matrix}\right] \]

    由上可知，\(\omega_n^i = cos\theta + isin\theta\)，我们假设 \(k_n^i=cos\theta-isin\theta\)，很容易的得到

\[\omega_n^i \cdot k_n^i=1 \]

    由此，我们还需要另一个重要的结论

\[\sum_{i=0}^{n-1}(\omega_n^k)^i=0 \]

    证明很简单，显然这个是等比数列求和，\(q=\omega_n^k\)
    \(\sum_{i=0}^{n-1}(\omega_n^k)^i=\frac{(1-q^n)(\omega_n^k)^0}{1-q}\)
    \(\because q^n=(\omega_n^k)^n=1\)
    \(\therefore \sum_{i=0}^{n-1}(\omega_n^k)^i=0\)

    当然，还有一个很简单的性质 \(^1\)，\(\omega_n^i=\omega_n^{i\%n}\).

    综上，我们可以构造一个矩阵了。

\[\left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &k_n^1 &k_n^2 &k_n^3 &\cdots &k_n^{n-1}\\ 1 &k_n^2 &k_n^4 &k_n^6 &\cdots &k_n^{2(n-1)}\\ 1 &k_n^3 &k_n^6 &k_n^9 &\cdots &k_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &k_n^{n-1}&k_n^{2(n-1)} &k_n^{3(n-1)} &\cdots &k_n^{(n-1)^2}\\ \end{matrix}\right] \]

    我们再思考一下，可以发现：

\[\left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &k_n^1 &k_n^2 &k_n^3 &\cdots &k_n^{n-1}\\ 1 &k_n^2 &k_n^4 &k_n^6 &\cdots &k_n^{2(n-1)}\\ 1 &k_n^3 &k_n^6 &k_n^9 &\cdots &k_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &k_n^{n-1}&k_n^{2(n-1)} &k_n^{3(n-1)} &\cdots &k_n^{(n-1)^2}\\ \end{matrix}\right] \left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right] {=} \left[\begin{matrix} n &0 &0 &0 &\cdots &0\\ 0 &n &0 &0 &\cdots &0\\ 0 &0 &n &0 &\cdots &0\\ 0 &0 &0 &n &\cdots &0\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 0 &0 &0 &0 &\cdots &n\\ \end{matrix}\right] \]

    终于，我们可以得到一个很优美的结论了。

\[` \left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &k_n^1 &k_n^2 &k_n^3 &\cdots &k_n^{n-1}\\ 1 &k_n^2 &k_n^4 &k_n^6 &\cdots &k_n^{2(n-1)}\\ 1 &k_n^3 &k_n^6 &k_n^9 &\cdots &k_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &k_n^{n-1}&k_n^{2(n-1)} &k_n^{3(n-1)} &\cdots &k_n^{(n-1)^2}\\ \end{matrix}\right] \left[\begin{matrix} y[0] \\ y[1] \\ y[2]\\ y[3]\\ \vdots\\ y[n-1]\\ \end{matrix}\right] {=} \left[\begin{matrix} n\cdot a[0] \\ n\cdot a[1] \\ n\cdot a[2]\\ n\cdot a[3]\\ \vdots\\ n\cdot a[n-1]\\ \end{matrix}\right] \]

    可以和第一步对比一下的，我相信，一定会有一个令人满意的结果的。
    我们只用把这些数进行一些适当的调整，然后再次进行一遍最开始的操作即可。

    到了这里，整个 算法的操作就已经叙述完毕了，最后让我们来看一看代码好了。

5.在 \(OI\) 中的快速傅里叶变换的代码实现

(详情可见代码中的注释部分，你可以结合上面的讲解和图片阅读)

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e6 + 5;
const double pi = acos(-1);
complex<double> a[maxn], b[maxn];
int n, m, x, len, L;
int rev[maxn];

void FFT(complex<double> *t, int mark)
{
    for(int i = 0; i < n; ++i) if(i < rev[i]) swap(t[i], t[rev[i]]);  // 将每个数放在它对应的位置上 
    for(int i = 1; i < n; i <<= 1){  // 枚举每段的长度 
        complex<double> wn(cos(pi / i), mark * sin(pi / i));
        for(int j = 0; j < n; j += 2 * i){  // 枚举每个段组 
            complex<double> w(1, 0);
            for(int k = j; k < j + i; k++, w *= wn){  // 枚举计算 
                complex<double> lin1 = t[k], lin2 = t[k + i] * w;
                t[k] = lin1 + lin2; t[k + i] = lin1 - lin2;
            }
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i <= n; i++) scanf("%d", &x), a[i] = x;
    for(int i = 0; i <= m; i++) scanf("%d", &x), b[i] = x;
    m += n; n = 1; while(n <= m) len++, n <<= 1;  //将多项式补齐 
    for(int i = 0; i < n; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));  //预处理出每个位置上的数是多少 
    FFT(a, 1), FFT(b, 1);
    for(int i = 0; i <= n; ++i) a[i] *= b[i];
    FFT(a, -1);
    for(int i = 0; i <= m; ++i) printf("%d ", (int)(a[i].real() / n + 0.5));
    return 0;
}

后记

    从开始准备到写到这里，一共用去了11天。觉得这是一件比较有意义的事情吧。当然，其中也有文化课等其他的事情，所以耗时比较久的才写完。在这里要感谢在这个过程中帮助过我的老师，学长和同学。很多时候都是在和他们讨论交流的过程中才逐渐完善我的想法和语言，很感谢他们。也希望在 \(OI\) 这条路上我能继续保持对一些东西的执念继续走下去吧。
    再次谢谢他们。
    谢谢大家。