《Python深度学习：基于PyTorch》学习记录 ：第1章 NumPy基础

声明：本篇仅作个人学习记录使用，如有侵权请联系删除
声明：本篇来源http://www.feiguyunai.com/index.php/2020/11/24/python-dl-baseon-pytorch-01/

​ 为什么是NumPy？实际上Python本身含有列表（list）和数组（array），但对于大数据来说，这些结构有很多不足。因列表的元素可以是任何对象，因此列表中所保存的是对象的指针。例如为了保存一个简单的[1,2,3]，都需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU等宝贵资源。 至于array对象，它直接保存数值，和C语言的一维数组比较类似。但是由于它不支持多维，在上面的函数也不多，因此也不适合做数值运算。
NumPy（Numerical Python 的简称）的诞生弥补了这些不足，NumPy提供了两种基本的对象：ndarray（N-dimensional array object）和 ufunc（universal function object）。ndarray是存储单一数据类型的多维数组，而ufunc则是能够对数组进行处理的函数。

1.1 生成NumPy数组

---

​ NumPy是Python的外部库，不在标准库中。因此，若要使用它，需要先导入NumPy。

import numpy as np

​ NumPy封装了一个新的数据类型ndarray（n-dimensional array），它是一个多维数组对象。该对象封装了许多常用的数学运算函数，方便我们做数据处理、数据分析等。如何生成ndarray呢？这里我们介绍生成ndarray的几种方式，如从已有数据中创建、利用random创建、创建特殊多维数组、使用arange函数等。

1.1.1 从已有数据中创建数组

• 将列表转换成ndarray

import numpy as np

list1 = [3.14, 20, -3.6, 0]
nda = np.array(list1)  # list to ndarray
print(type(nda),end=': ')
print(nda)

#output
#<class 'numpy.ndarray'>: [ 3.14 20.   -3.6   0.  ]

• 嵌套列表

import numpy as np

list1 = [[3.14, 20], [-3.6, 0],[3,6]]
nda = np.array(list1)  # list to ndarray
print(nda)

#output
#[[ 3.14 20.  ]
# [-3.6   0.  ]
# [ 3.    6.  ]]

1.1.2 利用random模块生成数组

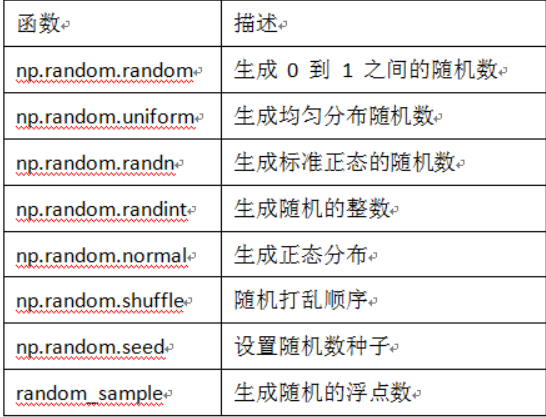
import numpy as np

nda1 = np.random.random([3,3])
print(nda1)
print("random ndarray shape :",nda1.shape)

#output
'''
[[0.82717024 0.17472656 0.79488477]
 [0.65796772 0.52120029 0.51912316]
 [0.56561377 0.43047079 0.36166983]]
random ndarray shape : (3, 3)
'''

import numpy as np

np.random.seed(114514)
nda = np.random.uniform(0,1,[3,3])
print(nda)

np.random.seed(114514)
nda = np.random.uniform(0,1,[3,3])
print(nda)

np.random.seed(2021)
np.random.shuffle(nda)
print(nda)

#output
'''
[[0.68775587 0.67617294 0.42661145]
 [0.78303236 0.78837491 0.03616564]
 [0.89739725 0.75986473 0.21021482]]
[[0.68775587 0.67617294 0.42661145]
 [0.78303236 0.78837491 0.03616564]
 [0.89739725 0.75986473 0.21021482]]
[[0.89739725 0.75986473 0.21021482]
 [0.78303236 0.78837491 0.03616564]
 [0.68775587 0.67617294 0.42661145]]
[[0.68775587 0.67617294 0.42661145]
 [0.78303236 0.78837491 0.03616564]
 [0.89739725 0.75986473 0.21021482]]
'''

1.1.3 创建特定形状的多维数组

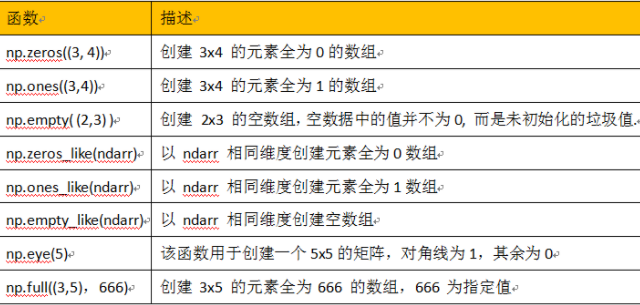
以上()均可用[]代替

**对数据进行保存和加载 **

import numpy as np

nda = np.full([6,6],114514)
print(nda)
np.savetxt(fname='./savenda.txt',X=nda)
ndaload = np.loadtxt('./savenda.txt')
print(ndaload)

1.1.4 利用arange、linspace函数生成数组

import numpy as np

nda = np.arange(0, 10, 2.2)
print(nda)
nda = np.arange(9, -1, -1)
print(nda)
nda = np.linspace(0,1,10)
print(nda)

#output
'''[0.  2.2 4.4 6.6 8.8]
[9 8 7 6 5 4 3 2 1 0]
[0.         0.11111111 0.22222222 0.33333333 0.44444444 0.55555556
 0.66666667 0.77777778 0.88888889 1.        ]
'''

​ 值得一提的，这里并没有像我们预期的那样，生成 0.1, 0.2, ... 1.0 这样步长为0.1的 ndarray，这是因为 linspace 必定会包含数据起点和终点，那么其步长则为(1-0) / 9 = 0.11111111。如果需要产生 0.1, 0.2, ... 1.0 这样的数据，只需要将数据起点 0 修改为 0.1 即可。
除了上面介绍到的 arange 和 linspace，NumPy还提供了 logspace 函数，该函数使用方法与 linspace 使用方法一样

1.2 获取元素

---

import numpy as np

np.random.seed(2021)
nd11 = np.random.random([10])
print(nd11)
# 获取指定位置的数据，获取第4个元素
print(nd11[3])
# 截取一段数据
print(nd11[3:6])
# 截取固定间隔数据
print(nd11[1:6:2])
# 倒序取数
print(nd11[::-2])
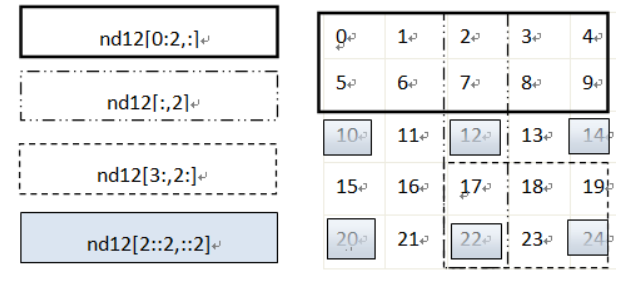
# 截取一个多维数组的一个区域内数据
nd12 = np.arange(25).reshape([5, 5])
print(nd12)
print(nd12[1:3, 1:3])
# 截取一个多维数组中，数值在一个值域之内的数据
print(nd12[(nd12 > 3) & (nd12 < 10)])
# 截取多维数组中，指定的行,如读取第2,3行
print(nd12[[1, 2]])  # 或nd12[1:3,:]
# 截取多维数组中，指定的列,如读取第2,3列
print(nd12[:, 1:3])

#output
'''
[0.60597828 0.73336936 0.13894716 0.31267308 0.99724328 0.12816238
 0.17899311 0.75292543 0.66216051 0.78431013]
0.31267308385468695
[0.31267308 0.99724328 0.12816238]
[0.73336936 0.31267308 0.12816238]
[0.78431013 0.75292543 0.12816238 0.31267308 0.73336936]
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]
 [20 21 22 23 24]]
[[ 6  7]
 [11 12]]
[4 5 6 7 8 9]
[[ 5  6  7  8  9]
 [10 11 12 13 14]]
[[ 1  2]
 [ 6  7]
 [11 12]
 [16 17]
 [21 22]]

进程已结束，退出代码 0
'''

获取数组中的部分元素除通过指定索引标签外，还可以使用一些函数来实现，如通过random.choice函数可以从指定的样本中进行随机抽取数据。

1.3 NumPy的算术运算

---

1.3.1 对应元素相乘

import numpy as np

A = np.array([[1, 2], [-1, 4]])
B = np.array([[2, 0], [3, 4]])
c = A*B
d = np.multiply(A,B)
print(c)
print(d)

#output
'''
 [[ 2  0]
 [-3 16]]
 
 [[ 2  0]
 [-3 16]]
'''

数组通过一些激活函数后，输出与输入形状一致。

import numpy as np

X = np.random.rand(2, 3)

def softmoid(x):
    return 1 / (1 + np.exp(-x))

def relu(x):
    return np.maximum(0, x)

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))

print("输入参数X的形状：", X.shape)
print("激活函数softmoid输出形状：", softmoid(X).shape)
print("激活函数relu输出形状：", relu(X).shape)
print("激活函数softmax输出形状：", softmax(X).shape)

#output
'''
输入参数X的形状： (2, 3)
激活函数softmoid输出形状： (2, 3)
激活函数relu输出形状： (2, 3)
激活函数softmax输出形状： (2, 3)
'''

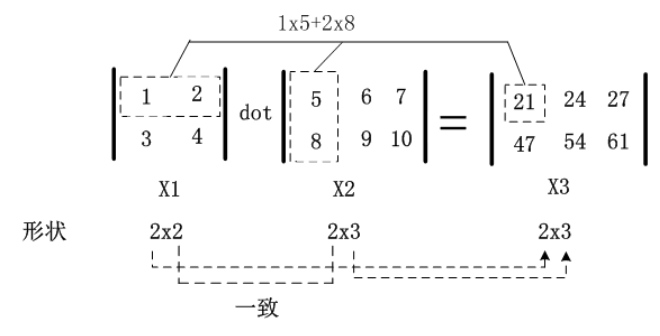
1.3.2 点积（内积，矩阵乘法）运算

import numpy as np

X1 = np.array([[1, 2], [3, 4]])
X2 = np.array([[5, 6, 7], [8, 9, 10]])
X3 = np.dot(X1, X2)
print(X3)

#output
'''
 [[21 24 27]
 [47 54 61]]
 '''

1.4 数组变形

---

​ 在机器学习以及深度学习的任务中，通常需要将处理好的数据以模型能接受的格式喂给模型，然后模型通过一系列的运算，最终返回一个处理结果。然而，由于不同模型所接受的输入格式不一样，往往需要先对其进行一系列的变形和运算，从而将数据处理成符合模型要求的格式。最常见的是矩阵或者数组的运算，经常会遇到需要把多个向量或矩阵按某轴方向合并，或需要展平（如在卷积或循环神经网络中，在全连接层之前，需要把矩阵展平）。

1.4.1 更改数组形状

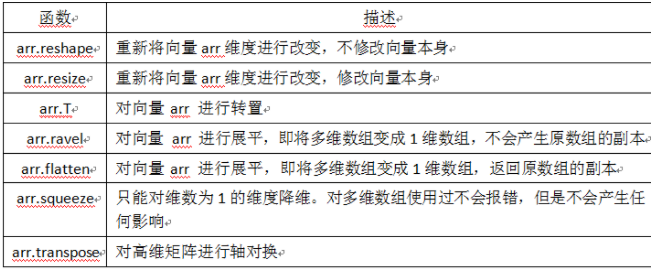
1.4.2 合并数组

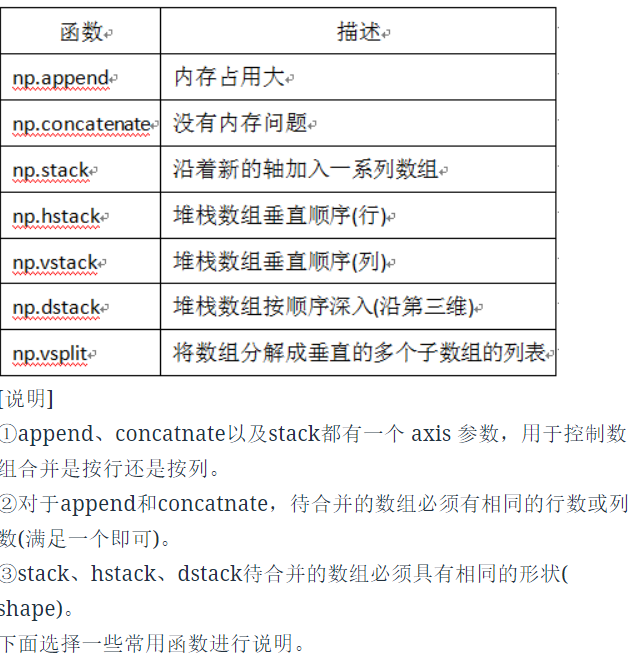
1.5 批量处理

---

​ 在深度学习中，由于源数据都比较大，所以通常需要采用批处理。如利用批量来计算梯度的随机梯度法（SGD），就是一个典型应用。深度学习的计算一般比较复杂，加上数据量一般比较大，如果一次处理整个数据，往往出现资源瓶颈。为了更有效的计算，一般将整个数据集分成小批量。与处理整个数据集的另一个极端是每次处理一条记录，这种方法也不科学，一次处理一条记录无法充分发挥GPU、NumPy平行处理优势。因此，实际使用中往往采用批量处理（mini-batch）。
如何把大数据拆分成多个批次呢？可采用如下步骤：
（1）得到数据集
（2）随机打乱数据
（3）定义批大小
（4）批处理数据集

import numpy as np

# 生成10000个形状为2X3的矩阵
data_train = np.random.randn(10000, 2, 3)
# 这是一个3维矩阵，第一个维度为样本数，后两个是数据形状
print(data_train.shape)
# (10000,2,3)
# 打乱这10000条数据
np.random.shuffle(data_train)
# 定义批量大小
batch_size = 100
# 进行批处理
for i in range(0, len(data_train), batch_size):
    x_batch_sum = np.sum(data_train[i:i + batch_size])
    print("第{}批次,该批次的数据之和:{}".format(i, x_batch_sum))

1.6 通用函数

---

NumPy提供了两种基本的对象，即ndarray和ufunc对象。前面我们介绍了ndarray，本节将介绍NumPy的另一个对象通用函数(ufunc)，ufunc是universal function的缩写，它是一种能对数组的每个元素进行操作的函数。许多ufunc函数都是用c语言级别实现的，因此它们的计算速度非常快。此外，它们比math模块中函数更灵活。math模块的输入一般是标量，但NumPy中函数可以是向量或矩阵，而利用向量或矩阵可以避免使用循环语句，这点在机器学习、深度学习中非常重要。表1-5为NumPy常用的几个通用函数。

1.7 广播机制

---

NumPy的Universal functions 中要求输入的数组shape是一致的，当数组的shape不相等的时候，则会使用广播机制。不过，调整数组使得shape一样，需满足一定规则，否则将出错。这些规则可归结为以下四条：
（1）让所有输入数组都向其中shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐；
如：a：2x3x2 b：3x2，则b向a看齐，在b的前面加1：变为：1x3x2
（2）输出数组的shape是输入数组shape的各个轴上的最大值；
（3）如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时，这个数组能够用来计算，否则出错；
（4）当输入数组的某个轴的长度为1时，沿着此轴运算时都用（或复制）此轴上的第一组值。
广播在整个NumPy中用于决定如何处理形状迥异的数组；涉及算术运算包括(+，-，*，/…)。这些规则说的很严谨，但不直观，下面我们结合图形与代码进一步说明：
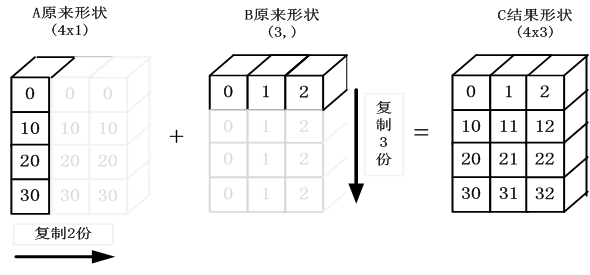
目的：A+B
其中A为4x1矩阵，B为一维向量 (3,)
要相加，需要做如下处理：
（1）根据规则1，B需要向看A齐，把B变为（1,3）
（2）根据规则2，输出的结果为各个轴上的最大值，即输出结果应该为（4,3）矩阵
那么A如何由（4,1）变为（4,3）矩阵？B如何由（1,3）变为（4,3）矩阵？
3）根据规则4，用此轴上的第一组值（要主要区分是哪个轴），进行复制（但在实际处理中不是真正复制，否则太耗内存，而是采用其它对象如ogrid对象，进行网格处理）即可，
详细处理如图1-4所示。