P4001 [BJOI2006]狼抓兔子

传送门

显然是网络流最小割

朴素的dinic会被卡

但是如果加上玄学优化就可以过了

主要是讲另一个方法

可以发现每条路径是不会交错的

对于样例的图，我们如果从右上随便走出发一条线到左下

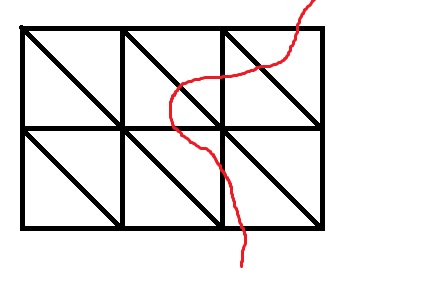
把线经过的边全部割掉，就是一种可行的方案

所以可以把每个平面看成点，点之间的边就是平面之间的公共边

只要我们从右上的一个虚节点出发，走到左下的一个虚节点

它的长度就是把路径经过的边割掉的代价

所以就可以跑最短路找最小代价了

重要的是怎么把图转化

 

首先把每个平面标号，然后慢慢找规律....

具体还是看代码吧

 

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
inline int read()
{
    int x=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return x;
}
const int N=2e6+7;
int fir[N],from[N<<2],to[N<<2],val[N<<2],cnt;//存转化后的图
inline void add(int a,int b,int c)
{
    from[++cnt]=fir[a];
    fir[a]=cnt;
    to[cnt]=b; val[cnt]=c;
}//连边
int n,m;
int dis[N];
struct node
{
    int u,v;
    bool operator < (const node &b) const{
        return u>b.u;
    }
};
priority_queue <node> q;
inline void Dijk()//最短路
{
    memset(dis,0x7f,sizeof(dis));
    dis[0]=0;
    q.push((node){0,0});
    while(!q.empty())
    {
        int u=q.top().u,v=q.top().v; q.pop();
        if(u!=dis[v]) continue;
        for(int i=fir[v];i;i=from[i])
        {
            int x=to[i];
            if(dis[v]+val[i]<dis[x])
            {
                dis[x]=dis[v]+val[i];
                q.push((node){dis[x],x});
            }
        }
    }
}
int main()
{
    int a,x,y;
    cin>>n>>m;
    //下面这些是可以慢慢推的...
    for(int i=1;i<=n;i++)
        for(int j=1;j<m;j++)
        {
            x=(i-2)*(m-1)*2+j*2-1; y=x+(m-1)*2+1;
            if(i==1) x=0,y=j*2;
            if(i==n) y=(n-1)*(m-1)*2+1;
            a=read();
            add(x,y,a); add(y,x,a);
        }
    for(int i=1;i<n;i++)
        for(int j=1;j<=m;j++)
        {
            x=(i-1)*(m-1)*2+j*2-1; y=x-1;
            if(j==1) y=(n-1)*(m-1)*2+1;
            if(j==m) x=0;
            a=read();
            add(x,y,a); add(y,x,a);
        }
    for(int i=1;i<n;i++)
        for(int j=1;j<m;j++)
        {
            x=(i-1)*(m-1)*2+j*2; y=x-1;
            a=read();
            add(x,y,a); add(y,x,a);
        }
    Dijk();
    printf("%d",dis[(n-1)*(m-1)*2+1]);
    return 0;
}